Примеры некоторых распределений

1. Биномиальное распределение. Дискретная случайная величина ξ с конечным числом возможных значений x_k=k=0,1,2,…,n называется распределенной по биномиальному закону, если соответствующие вероятности даются формулой Бернулли

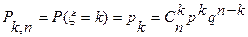. (1)

По биномиальному закону распределено, например, число успехов в n испытаниях Бернулли (см §7.). Воспользуемся биномом Ньютона

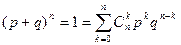. (2)

Из (2) видно, что формула (1)- это k-й член разложения бинома Ньютона. Отсюда и название распределения. Из этой же формулы (2) видно, что .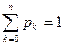

Найдем математическое ожидание.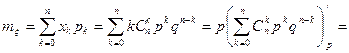

.

(Индекс внизу означает, что производная берется по p).

Итак, 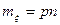. (3)

Для вычисления дисперсии воспользуемся формулой

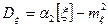. (4)

Продифференцируем (2) по p два раза и умножим полученное равенство на p². В результате получим

,

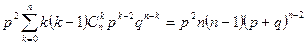или ,

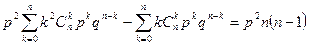или 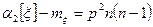. (5)

Подставляя 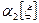из (5) в (4), найдем с учетом (3)

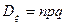. (6)

Можно доказать, что мода М₀ случайной величины ξ, распределенной по биномиальному закону, удовлетворяет условию

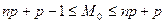. (7)

В частности, если 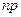число натуральное, то оно и является модой. Коэффициент асимметрии определяется формулой

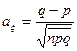. (8)

1. Геометрическое распределение. Дискретная случайная величина ξ, возможными значениями которой является бесконечная последовательность натуральных чисел 1,2,3,…, а соответствующие вероятности даются формулой

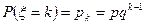, (9)

называется распределенной по геометрическому закону. Если число испытаний Бернулли не ограничивать, а проводить их до первого успеха, то число всех испытаний (вплоть до первого успеха) есть случайная величина ξ, распределенная по геометрическому закону. Название закона обязано тому, что вероятности (9) образуют геометрическую прогрессию со знаменателем q.

Проверим условие 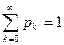. Действительно,

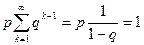. (10)

Найдем математическое ожидание

.

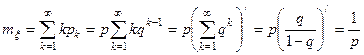Итак, 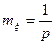. (11)

Для нахождения дисперсии вычислим сначала 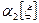. Из (10) получим 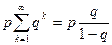. Продифференцировав последнее тождество два раза по q и умножив обе части полученного равенства на q, найдем

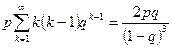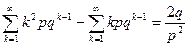, или

, или

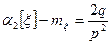. (12)

Подставляя 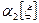из (12) в (4) и учитывая (11), получим

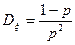. (13)

Пример 1. Сколько в среднем расходуется патронов, чтобы поразить цель, если вероятность попадания p=0,2, а цель поражается при первом же попадании?

Решение. Воспользуемся (11), получим 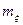=5.

2. Распределение Пуассона. Дискретная случайная величина ξ, возможными значениями которой являются члены последовательности 0,1,2,…, а соответствующие вероятности даются формулой

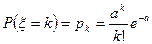, (14)

называется распределенной по закону Пуассона, 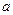– параметр.

В §7 доказано, что закон Пуассона является предельным для биномиального, его называют законом редких явлений. По закону Пуассона может быть распределено, например, число телефонных звонков, поступивших на телефонную станцию за некоторый промежуток времени.

Убедимся, что 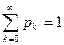. Действительно,

.

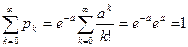Найдем математическое ожидание

= = .

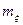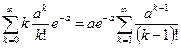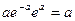Итак, 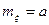. (15)

Чтобы найти дисперсию, вычислим предварительно второй начальный момент .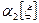

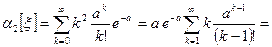
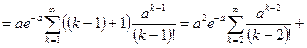
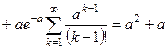. (16)

Подставляя (16) и (15) в (4), найдем

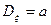. (17)

Таким образом, при распределении Пуассона .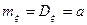

Пример 2. Среднее число отказов аппаратуры за год равно 3. Определить вероятность отказа аппаратуры в течение месяца.

Решение. Очевидно, 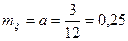. Пусть событие А означает нуль отказов за месяц. Тогда согласно (14) 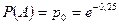. Событие 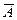означает отказ аппаратуры (хотя бы один отказ). .

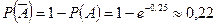3. Равномерное распределение. Если все возможные значения непрерывной случайной величины ξ лежат в

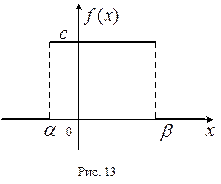
конечном интервале (α, β), а плотность вероятности постоянная на этом интервале (см. рис. 13), то говорят, что случайная величина ξ распределена равномерно (см.§9). Плотность распределения можно записать так

.

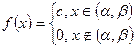Постоянную с найдем, используя свойство плотности распределения 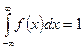. В нашем случае 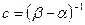. Найдем математическое ожидание

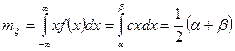. (18)

Аналогично найдем дисперсию

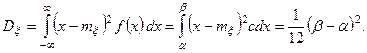(19)

Из (18) видно, что кривая распределения симметрична относительно центра распределения, поэтому все центральные моменты нечетного порядка обращаются в нуль. Медиана совпадает с .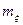

Пример 3. Автобусы ходят с интервалом 5 минут. Найти вероятность того, что случайно подошедший к остановке пассажир будет ожидать автобус не более 3-х минут.

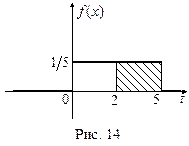
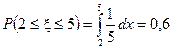Решение. (см. рис. 14).

4. Показательный закон. Непрерывная случайная величина распределена по показательному закону, если ее плотность имеет вид

λ>0 – параметр (см. рис. 15). Найдем функцию распределения

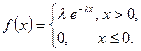
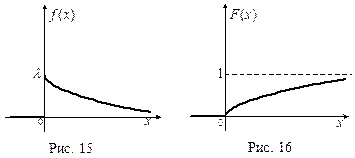(см. рис.16).

Найдем математическое ожидание 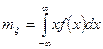. Интегрируя по частям, получим

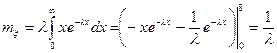. (20)

Найдем дисперсию

.

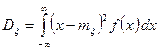После двукратного интегрирования по частям получим

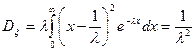. (21)

Коэффициент асимметрии 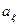и медиана 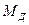определяются формулами

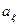=2, 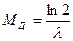. (22)

Упражнение. Проверить условие 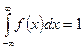и формулы (22).

Время безотказной работы многих электронных приборов подчиняется показательному закону.

Пример 4. Определить вероятность того, что аппаратура безотказно проработает не менее 3-х лет, если ее среднее время безотказной работы 2 года.

Решение. По условию задачи , .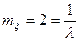

.

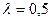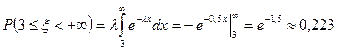5. Гамма-распределение. Этот закон распределения является обобщением показательного. Плотность гамма - распределения определяется формулой

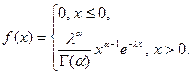(23)

Параметры a и l могут быть любыми положительными числами, 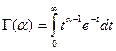- гамма – функция (см. §1 гл.4). При a=1 гамма-распределение совпадает с показательным распределением.

Используя свойства гамма – функции, найдем математическое ожидание и дисперсию.

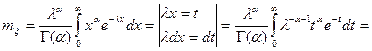
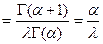. Итак,

. (24)

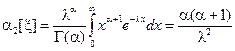, (25)

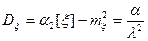. (26)

Мода М₀ и коэффициент асимметрии 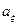определяются формулами

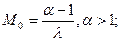
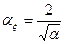. (27)

Распределение хи-квадрат с n степенями свободы является частным случаем гамма – распределения. Плотность этого распределения определяется формулой (23) при l=0,5, a=0,5n. Числовые характеристики также получаются по соответствующим формулам (24-27) при l=0,5, a=0,5n.

По закону хи-квадрат с n степенями свободы распределена, например, сумма n квадратов случайных величин ξ_i, подчиненных некоторым дополнительным условиям.

6. Нормальное распределение. Если плотность распределения непрерывной случайной величины ξ определяется формулой

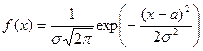, (28)

то говорят, что случайная величина распределена по нормальному закону (по закону Гаусса) с параметрами 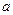и σ. Обозначают N(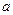,σ). Если 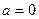, 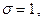то закон называется стандартным нормальным и обозначается N(0,1).

Нормальный закон распределения играет исключительную роль в теории вероятностей. Исключительное положение этого закона объясняется тем, что он является предельным законом, к которому стремятся многие другие законы распределения. Это утверждение носит название центральной предельной теоремы, с которой мы познакомимся позже.

Кривая распределения (28) симметрична относительно точки х=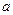. При изменении параметра 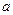кривая смещается вдоль оси Ох, не меняя своего вида. В точке х=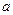кривая достигает своего максимума 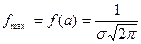. При уменьшении σ величина 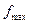увеличивается, а т.к. площадь, ограниченная кривой распределения, остается равной единице, то кривая сжимается с уменьшением σ. Точки х=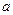±σ являются ее точками перегиба, ось Ох – асимптотой. Найдем математическое ожидание.

.

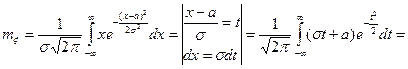
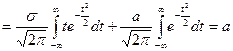Воспользовались интегралом Пуассона

,

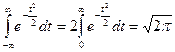а первое слагаемое обращается в нуль, т.к. подынтегральная функция нечетная. Итак,

m_ξ=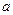 (29)

Очевидно, математическое ожидание, мода и медиана совпадают. Найдем центральные моменты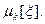

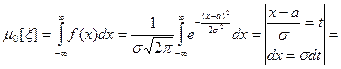
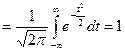. Тем самым мы проверили основное свойство плотности распределения. Первый центральный момент 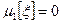для любого распределения, поэтому найдем 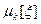при k≥2.

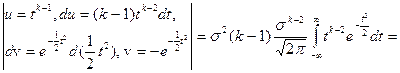
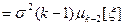. Итак,

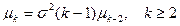. (30)

Из (30) найдем 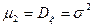, т.е. параметр 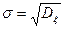есть среднее квадратичное отклонение. Из равенства 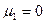и (30) следует, что все центральные моменты нечетного порядка обращаются в нуль. Легко проверить, что эксцесс 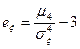для нормального распределения равен нулю. Все другие кривые распределения сравнивают с кривой нормального распределения. Если 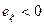, то кривая распределения более плосковершинная по сравнению с гауссовой кривой, при - более островершинная.

Неэлементарная функция 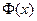, определенная несобственным интегралом

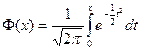, (31)

называется интегралом вероятности. Выразим функцию распределения F(x) через интеграл вероятности.

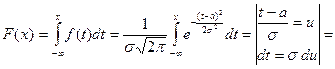
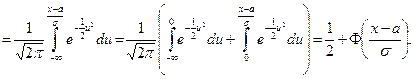
Итак, 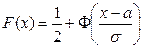. (32)

Из (32) получим

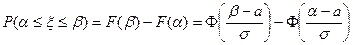.(33)

Пример 5. Найти вероятность события если случайная величина 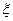распределена нормально.

Решение. Р(|ξ-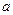|>3σ)=1-Р(|ξ-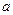|≤3σ)=1-Р(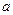-3σ≤ξ≤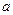+3σ) = =1-Ф(3)+Ф(-3)=1-2Ф(3)=1-2·0,49865=0,0027. Значение Ф(3) взято из таблиц.

Таким образом, для нормально распределенной величины все ее практически возможные значения ограничены интервалом (m_ξ-3σ_ξ, m_ξ+3σ_ξ), а событие 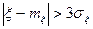оказывается практически невозможным. Этот факт носит название “правила трех сигма”.

Дата добавления: 2014-01-07