Понятие регрессии

Рассмотрим двумерную случайную величину (ξ,η). Пусть, например, ξ - рост человека, а η - его вес. Ясно, что между весом и ростом существует зависимость, но эта зависимость вероятностная, ее нельзя записать в виде функции. Однако зависимость усредненных величин можно записать в виде функции. Если плотность f(x,y) непрерывной случайной величины известна, то можно найти условные плотности f₁(x/y), f₂(y/x) и условные математические ожидания

(1)

(2)

В нашем примере М[hïx] -это средний вес людей, рост которых одинаковый, x=x; а M[xïy] - это средний рост людей одинакового веса, h=y.

Формулы (1) и (2) дают функциональную зависимость условных математических ожиданий одной случайной величины от возможных значений другой. Функция y=g(x) называется регрессией величины h на x, а функция x=q(y) - регрессией величины x на h. Графики функций g(x) и q(y) называются кривыми регрессии.

Аналогично можно найти и другие условные числовые характеристики, например, условную дисперсию

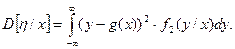(3)

Условная дисперсия D[h/x] определяет рассеяние случайной величины h/x относительно регрессии g(x). Т.к. эта дисперсия является функцией возможных значений случайной величины x (D[h/x]=j(x)), т.е. величиной случайной, то ее усредняют, находят ее математическое ожидание. В результате усреднения получим:

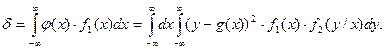(4)

Здесь f₁(x) - плотность распределения случайной величины x. С учетом того, что f₁(x)f₂(y/x)=f(x,y), формула (4) принимает вид:

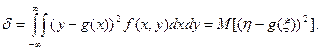(5)

Как видно из (5), d - это безусловная дисперсия случайной величины h относительно своего центра распределения g(x). Известно, что дисперсия(рассеяние) относительно центра распределения минимальная. Отсюда вывод: если регрессию g(x) взять в качестве оценки зависимости h от x (h≈g(x)), то это будет наилучшая оценка этой зависимости в смысле минимума средней квадратичной погрешности.

Если случайная величина (x,h) дискретная с конечным числом возможных значений, то условные математические ожидания вычисляются по формулам:

(6)

(7)

Пример 1. Найти условные математические ожидания M[ξ/y₁] и M[ξ/y₂] случайной дискретной величины (x,h) примера 1 §14.

Решение: условные законы распределения случайных величин ξ/y₁ и ξ/y₂ найдены в примере 1 §15. Используя эти законы, по формуле (7) найдем

M[ξ/y₁]=1×0,30+3×0,12+4×0,5+8×0,08=3,3,

M[ξ/y₂]=1×0,6+3×0,2+4×0,06+8×0,14=2,56.

Пример 2. Случайная величина (x,h) задана своей плотностью распределения

Найти регрессии h на x и x на h.

Решение. Условные плотности f₂(y/x) и f₁(x/y) найдены в примере 2 §15. Используя их, по формулам (1) и (2) найдем

Итак, y=g(x)= -x/3 - это регрессия h на x.

Аналогично

Таким образом, x=q(y)=2-3y/4 - регрессия x на h.

Как видно, обе регрессии линейные (см. рис. 20). Можно доказать, что если закон распределения случайной величины (x,h) нормальный, то регрессии x на h и h на x

будут линейными, а прямые регрессии проходят через центр симметрии (m_ξ,m_η).

Пример 3. Найти регрессии, если случайная величина (x,h) задана своей плотностью распределения

Решение. Найдем сначала плотности распределения компонент ξ и η вектора (ξ,η):

Найдем теперь условные плотности распределения:

Заметим, что данная и все найденные плотности распределения отличны от нуля только в первом квадранте.

Согласно формулам (1) и (2) найдем:

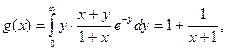
Итак, y=g(x)=1+1/(1+x) и x=q(y)=1+1/(1+y) - регрессии соответственно h на x и x на h. Кривые регрессии изображены на рисунке 21.

Дата добавления: 2014-01-07