Основні поняття теорії ґрат

ЛЕКЦІЯ 10.Відношення порядку

Відношення часткового порядку визначається як відношення, що задовольняє наступним трьом властивостям:

Р1. x £ x – рефлексивность,

Р2. якщо x £ y і y £ x, то x = y – антисиметричність,

Р3. якщо x £ y і y £ z, то x £ z – транзитивність.

Наприклад, відношення включення безлічей A Í B, тобто “ A – підмножина B ”, є відношенням порядку. Для нього виконуються всі перераховані вище властивості:

A Í A – будь-яка безліч включена саме в себе;

якщо A Í B і B Í A, те A = B, тобто безлічі A і B рівні;

якщо A Í B і B Í C, то A Í C, – властивість транзитивності неважко перевірити за допомогою діаграм Венна.

У загальному виді відношення порядку позначається символом £.

Якщо в упорядкованій безлічі для будь-яких двох елементів не виконується властивість рефлексивности, тобто x £ y і x ¹ y, то таке відношення називається відношенням строгого порядку і позначається x < y. Наприклад, відношення “ x – предок y ”, визначене на безлічі всіх людей, є відношення строгого порядку.

Безліч, на якому визначене відношення часткового порядку, називається частково упорядкованою безліччю.

У частково упорядкованій безлічі не кожні два елементи знаходяться у відношенні порядку; у такій безлічі є непорівнянні елементи. Як приклад розглянемо безліч усіх підмножин безлічі P = {a, b, c}, тобто множина-ступінь Ã(Р) = {Æ, { a }, { b }, { c }, { a, b }, { a, c }, { b, c }, { a, b, c }}. Це частково упорядкована безліч по відношенню включення: { a } Í { a, b }, { a } Í { a, b, c }, { a, b } Í { a, b, c }, Æ Í { a }, Æ Í { b }, Æ Í { c }, і так далі, однак безлічі { a }, { b }, { c } і безлічі { a, b }, { a, c }, { b, c } непорівнянні.

Безліч, у якому для будь-яких двох елементів існує відношення порядку, називають лінійно упорядкованою безліччю, або ланцюгом. Для таких безлічей виконується властивість

P4. " x, y: x £ y або y £ x.

Наприклад, безліч натуральних чисел є ланцюгом; підмножина A = { Æ, { a }, { a, b }, { a, b, c }} безлічі Ã(Р) з відношенням порядку Æ Í { a } Í { a, b } Í { a, b, c } утворить ланцюг.

Оскільки властивості P1, P2, P3 задають найбільш загальний тип порядку, частково упорядковані безлічі називають просто упорядкованими, на відміну від лінійно і строго упорядкованих безлічей.

Упорядковані безлічі прийнята зображувати у виді спеціальних графів – діаграм Хассе.

Говорять, що “ a покриває b ” в упорядкованій безлічі X, якщо b £ a і не існує такого x Î X, щоб b £ x £ a. Тоді упорядкована безліч можна зобразити у виді графа, що будується знизу нагору: якщо елемент b покриває елемент a, те він розташовується вище елемента a і з'єднується з ним прямій. Отриманий граф називається діаграмою упорядкованої безлічі, або діаграмою Хассе (див. мал. 1).

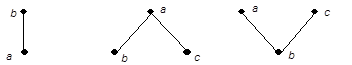
a) b) c)

Рис. 1.

а). b покриває a; b). а покриває b і з; с). а, з покривають b.

Діаграма Хассе може бути отримана з ориентированого графа відносини порядку x £ y, де x, y Î X, видаленням петель і транзитивно замикаючих дуг. Якщо два елементи a, b Î X знаходяться у відношенні порядку a £ b, то на діаграмі існує шлях з а в b. Таким чином, будь-яка кінцева упорядкована безліч з точністю до ізоморфізму визначається своєю діаграмою.

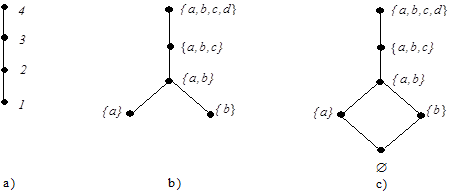
Рис. 2. Приклади діаграм Хассе

На мал. 2-а зображена діаграма ланцюга натуральних чисел { 1, 2, 3, 4 }, на мал. 2- b – діаграма безлічі S = {{ a }, { b }, { a, b }, { a, b, c }, { a, b, c, d }}, упорядкованого відношенням включення. Ми бачимо, що кожен вышележащий елемент на діаграмі “більше” усіх, лежачих нижче його. Таким чином, немає необхідності стрільцями указувати відношення порядку між елементами: це легко визначити за рівнем, що займає кожен елемент на діаграмі Хассе. Тому діаграма Хассе звичайно зображується без стрілок.

Якщо в упорядкованій безлічі X існує єдиний елемент а, такий що " x Î X (а £ х), то а називається найменшим елементом упорядкован-безлічі, або инфимумом безлічі (позначається inf). Якщо існує єдиний елемент b, такий що " x Î X (x £ b), то b називається найбільшим елементом, або супремумом безлічі X (позначається: sup).

З визначень випливає, що будь-яка упорядкована безліч може мати тільки один найменший і один найбільший елемент. Ці елементи часто називають нулем і одиницею упорядкованої безлічі відповідно, і позначають 0 і I.

На мал. 2-а inf=1 і sup=4; на мал.2- b sup= {a, b, c, d}, а inf відсутній. Однак, оскільки будь-яка безліч містить у собі порожня безліч, ця діаграма може бути добудована так, як показано на мал. 2-з.

Упорядкована безліч, у якому існують найбільший і найменший елементи, називають упорядкованою безліччю з нулем і одиницею. Тоді. будь-який інший елемент безлічі лежить між нулем і одиницею, тому елементи 0 і I, якщо вони існують, називаються універсальними гранями безлічі Р.

Мінімальним елементом упорядкованої безлічі X називається такий елемент а, що ні для якого x Î X не виконується умова x £ а, а максимальним елементом називається такий елемент b, що ні для якого x Î X не виконується умова b £ x.

Неважко показати, що найменший елемент завжди є мінімальним в упорядкованій безлічі, а найбільший – максимальним, але зворотне здійсненно далеко не завжди. У розглянутому вище прикладі на мал. 2- b безліч { a, b, c, d } є найбільшим елементом і, у той же самий час, максимальним, а безлічі { a } і { b } є мінімальними елементами, у той час як найменшого елемента в цій безлічі не існує.

Будь-який кінцевий ланцюг містить найбільший і найменший елементи, що є мінімальним і максимальним елементами.

Дата добавления: 2014-01-07