Методы определения кратчайших путей с помощью нумерации узлов и ветвей

Метод, предложенный Фордом [] позволяет определить кратчайший путь от произвольного узла 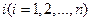к фиксированному узлу N. Исходными данными для определения кратчайших путей является, как и обычно, структурная матрица длин 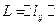рассматриваемой сети. Алгоритм определения кратчайших путей по этому методу состоит в выполнении следующих действий:

1) фиксированному узлу N приписывается вес 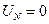, а произвольному узлу сети вес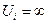

2) выбирается произвольный узел и сравнивается его вес 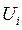с суммой веса 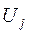, соседнего узла и длины ветви , соединяющей выбранный узел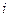с узлом .

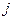Если

, (5.1)

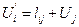то прежний вес узла заменяется на , в противном случае вес узла остается прежним.

Указанная процедура пересчета узлов производится до тех пор, пока хотя бы для одного узла 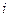выполняется неравенство (5.1)

Веса узлов после пересчета будут соответствовать длине кратчайшего пути узла 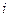к фиксированному узлу N.

Повторяя указанную процедуру для различных фиксированных узлов 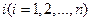, можно получить величины кратчайших путей между всеми узлами сети.

Описанный метод содержит один из способов получения 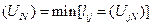, так как последовательная проверка неравенства (5.1) и замена веса узла на меньший вес приводит к тому, что вес узла .

Пример. Пусть задана сеть, содержащая п = 4 узла, структур­ная матрица длин которой

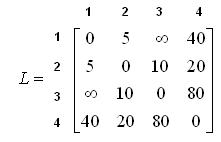
(граф, отображающий рассматриваемую сеть, представлен на рис. 5.1; цифры, стоящие у каждого ребра графа, обозначают его длину)

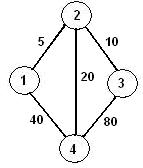
Рис. 5.1

Необходимо определить кратчайшие пу­ти к узлу 1. Для этого:

1) приписываем узлу 1 вес , а всем остальным узлам веса

2) просматриваем все пары узлов (i, j) и проверяем выполнение неравенства (5.1)

При i = 2, j = 1, 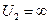, , неравенство удовлетворяется и уз­лу 2 приписываем вес .

При i = 3, j = 1, 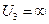, , 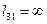неравенство (5.1) заведомо не

удовлетворяется.

Поэтому все пары узлов, для которых 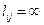, рассматривать не следует, так как при 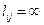неравенство никогда не будет удовлетворяться и вес узла останется прежним.

При i = 4, j = 1, 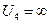, , 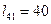неравенство удовлетворяется и узлу 4 приписываем веc .

При i = 3, j = 2, 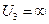, , 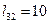неравенство удовлетворяется и узлу 3 приписываем вес .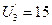

При i = 4, j = 2, , , 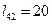неравенство 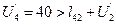удовлетворяется и узлу 4 приписываем вес .

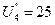Нетрудно убедиться, что больше ни для одной пары узлов нера­венство (5.1) не удовлетворяется. Поэтому полученные веса узлов , , , 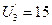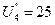являются искомыми кратчайшими расстояниями к узлу 1.

Веса узлов определяют только величину кратчайшего рас­стояния от узла i к фиксированному узлу N. Для определения самого пути (последовательности узлов или ветвей, составляющих этот путь) можно использовать дополнительную процедуру, которая использует свойство веса узла i, состоящее в том, что существует узел 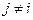, для которого выполняется равенство

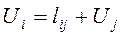, (5.2)

откуда следует, что если

, (5.3)

то ветвь, соединяющая узлы i и j сети, лежит на кратчайшем пути от узла i к узлу N. Определяя затем ветвь, удовлетворяющую усло­вию (5.3) на узле j и т. д., можно определить последовательность ветвей, составляющих путь от узла i к узлу N. Легко видеть, что этот путь является кратчайшим. Так как указанная процедура яв­ляется в некотором роде обратным процессом по отношению к нумерации узлов, то способ определения кратчайших путей получил название «обратного вычитания».

При определении кратчайшего пути от узла 3 к узлу 1 в рас­сматриваемом ранее примере легко убедиться, что единственной ветвью, исходящей из узла 3 и удовлетворяющей условию (5.3), является ветвь, соединяющая узлы 3 и 2, так как

;

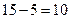
Следовательно, кратчайший путь от узла 3 проходит по ветви к узлу 2. На узле 2 ветвью, удовлетворяющей условию (5.3), является ветвь, соединяющая узлы 2 и 1:

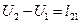; 5 - 0 = 5

Таким образом, кратчайший путь от узла 3 к узлу 1 проходит, через узел 2 и будет использовать ветви, соединяющие узлы 3 и 2, 2 и 1.

Так как в описанном методе получаются только первые кратчайшие пути, которые заведомо не содержат петель, то проблема выявления и ликвидации петель в этом случае не возникает.

Дата добавления: 2014-01-07