Метод Дийкстра

Метод Дийкстра является итерационным. Пусть на k -м шаге итерации полу­чены кратчайшие пути между каждым узлом коммутации (УК), образовавшие некото­рое подмножество N, и 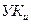,в который включен источник инфор­мации.

На (k + 1)-м шаге к мно­жеству N добавляется такой УК, расстояние от которого до 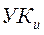- кратчайшее по сравнению с рас­стояниями до 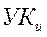от других УК, не включенных в множество N.

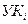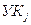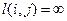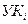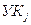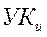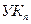Пусть l (i, j) длина пути от к , причем , если между и нет ветви. Пусть D (п) - длина кратчай­шего пути от до , прохо­дящего только через УК, принад­лежащие множеству N. Для про­стоты обозначим 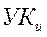через 1, а остальные узлы — через 2, 3,...

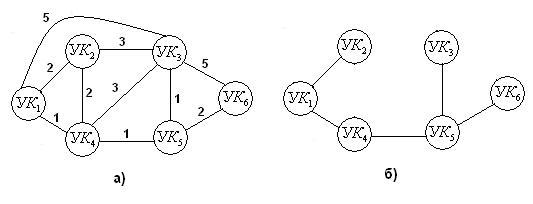
Рис. 6.1

Процедура нахождения кратчайших путей от всех узлов к 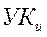состоит в следующем:

1. Вначале образуется множество N = {1} и для каждого 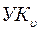, не входящего в N, принимается .

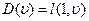2. На каждом последующем шаге находится 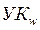, не входящий в множество N, для которого D (w) есть минимальное число; этот 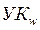включается в множество N. Затем обновляется значение рас­стояния 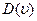для оставшихся узлов, не вошедших в множество N:

,

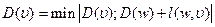т. е. новое значение 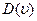будет равно минимальному значению из двух возможных: старого значения 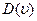и суммы .

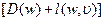Рассмотрим применение алгоритма к сети, изображен­ной на рис. 6.1, а где цифры на ветвях указывают их длину. Порядок вычисле­ний по этому методу ясен из табл. 6.1.

Из табл. 6.1 видно, что в исходном состоянии на кратчайшем расстоянии от 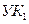(т. е. от 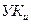) будет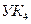. Поэтому па первом шаге 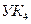включается в множество N. Теперь из оставшихся УК ближе всего к 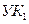будет находиться 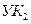, причем на таком расстоянии он был и до включения 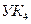в множество N. Поэтому в дереве кратчайших путей (см. рис. 6.1, б) как 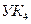, так и 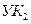под­ключены непосредственно к 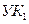. Таким образом, на втором шаге в множество N добавляется .

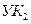На втором шаге, следующим кратчайшим путем до 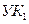будет путь от 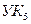. При этом из табл. 6.1 видно, что значение 2 сменило 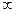после включения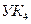

Таблица 6.1

Шаг итерации	Множество N	D (2)	D (3)	D (4)	D (5)	D (6)
Исходное Состояние	{1} {1, 4} {1, 2, 4} {1, 2, 4, 5} {1, 2, 3, 4, 5} {1, 2, 3, 4, 5, 6}

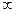
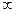
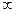
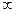
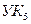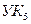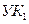в множество N. Следовательно, в дереве кратчайших путей прямой ветви не имеется, а кратчайший путь от до проходит через .

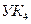Аналогично заполняются другие строки табл. 6.1, и постепенно строится дерево кратчайших путей, окончательный вид которого представлен на рис. 6.1, б. По дереву путей легко получить примитивную матрицу маршрутов при связи от 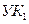до всех остальных УК сети. Для рассматриваемого примера эта матрица имеет вид

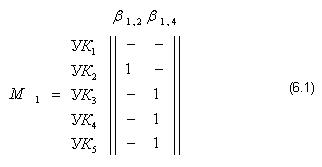
Очевидно, что этот метод можно использовать для нахождения кратчайших путей от всех УК к общему входящему УК_В.

Матрица маршрутов называется примитивной, если в ней указаны только основные пути, соответствующие, например, кратчайшим путям; в примитивной матрице маршрутов, очевидно, обходные пути не указаны.

Для получения дерева путей по методу Дийкстра, как и для матричного метода, требуется информация о состоянии всей сети. При использовании же метода Форда и Фалкерсона строится дере­во путей, на котором указываются кратчайшие расстояния от всех узлов к одному определенному УК (в нашем случае 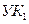). При этом для построения такого дерева необходима информация толь­ко от соседних УК (об их весе) и сведения о длине исходящих ветвей. Поэтому данный метод может быть использован для созда­ния распределенной системы динамического управления потоками.

Используя тот или иной метод, коррекцию матриц маршрутов можно осуществлять периодически либо только при существенном изменении ситуации на сети пакетной коммутации, например при повреждении линий.

Дата добавления: 2014-01-07