Алгоритм Гомори-Ху

Если пропускная способность каждой дуги не зависит от направления движения потока по этой дуге и если каждую пару узлов можно рассматривать как пару источник – сток, то общее число задач о максимальном потоке, которое должно быть решено, равно 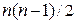, где 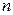- число узлов в сети. При работе алгоритма Гомори – Ху максимальный поток определяется только 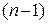раз.

Пусть G = (N,A) – неориентированная сеть, где N – множество узлов, A – множество дуг. Пусть 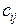- пропускная способность дуги (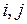) из множества A, и пусть 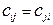. Предположим также, что множество узлов задается в виде N = {1,2,...,n}. При описании алгоритма будут использоваться следующие обозначения:

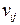- максимальный поток между узлами 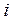и ;

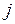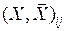- максимальный разрез, отделяющий 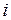от ();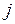

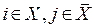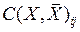- пропускная способность минимального разреза, отделяющего 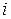от .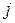

Если некоторый узел s рассматривать как источник, а другой узел t – как сток, то, согласно теореме о максимальном потоке и минимальном разрезе,

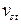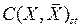= . Если затем в качестве источника и с тока выбирается другая пара узлов (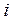и 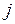соответственно), удовлетворяющих одному простому условию, то в алгоритме Гомори – Ху при определении величины 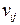используется решение задачи о максимальном потоке, найденное на предыдущем шаге. А именно, если узлы 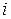и 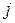выбираются таким образом, что оба они принадлежат X (или 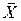), то множество узлов 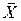(или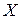, есл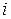и и 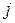принадлежат 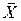) может быть объединено в один узел. При этом величина максимального потока из 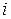в 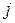будет одной и той же для исходной и конденсированной сетей.

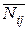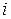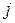Пусть - множество узлов, образованное в результате конденсации всех узлов, лежащих по ту сторону разреза, где не содержатся узлы и . Пусть 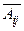- множество дуг, соединяющих узлы из 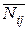. Тогда модифицированная сеть может быть представлена в виде 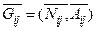. Если известны пропускные способности дуг, принадлежащих 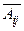, то для нахождения величины максимального потока между узлам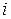и и 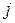можно воспользоваться процедурой расстановки пометок. Эти пропускные способности мы определим с помощью следующей простой процедуры. Пусть 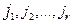- узлы из 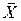, непосредственно связанные с узлом 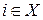. Если конденсируется множество 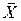, то дуги 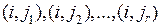заменяются одной дугой, соединяющий узел 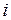и конденсированный узел 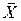. Пропускная способность этой дуги вычисляется следующим образом:

.

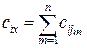Как отмечалось выше, величина максимального потока из 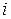в 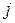может быть вычислена с помощью процедуры расстановки пометок, примененной к сети 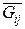. Для определения величины 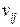вновь необходимо найти минимальный разрез, отделяющий 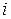от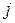. Пусть 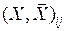- соответствующий разрез с минимальной пропускной способностью. Теперь можно выбрать другую пару узлов, принадлежащую либо 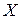, либо 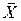, и построить другую конденсированную сеть. В результате выполнения процедуры расстановки пометок можно будет определить другой разрез и построить новую конденсированную сеть. Можно показать, что, после того как будет выбрана 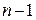пара узлов, мы определим все 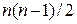величин максимального потока для исходной сети .

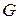Блок – схема алгоритма Гомори – Ху изображена на рис. 3.3. Основная идея алгоритма состоит в интерактивном построении максимального остовного дерева, ветви которого соответствуют разрезам, а параметры ветвей -величинам разрезов. Ниже приводится обоснование алгоритма и приводится иллюстративный пример.

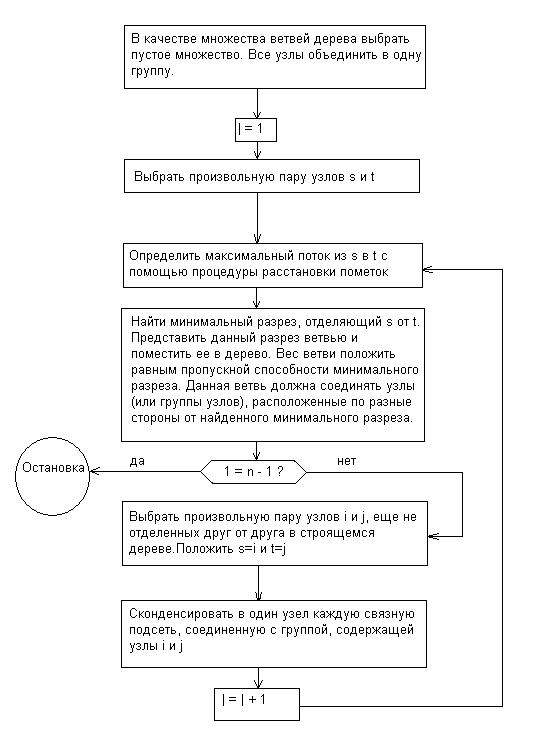
Рис. п1.1. Блок – схема алгоритма Гомори – Ху.

Обоснование алгоритма.

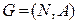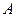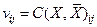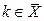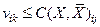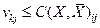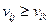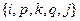Пусть - неориентированная сеть, и пусть пропускные способности всех дуг из удовлетворяют условию . Пусть . Согласно теореме о максимальном потоке и минимальном разрезе, . Если , то , а если , то . Следовательно, и , откуда следует, что , где - связное множество узлов из N. Следовательно . В общем случае

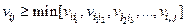, (п1.1)

где 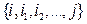- связное множество узлов из N.

Перед тем как продолжить наши рассуждения, докажем следующие свойства максимального остовного дерева:

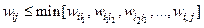, (п1.2)

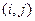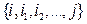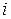где - произвольная дуга, не принадлежащая данному дереву, - единственная последовательность узлов, соединяющих ветви дерева, - вес дуги сети. Если неравенство (п1.2) не верно, то вместо любой дуги пути из в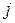можно взять дугу 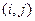, в результате чего будет построено дерево с большим весом. Данное противоречие доказывает справедливость неравенства (п1.2).

Если веса дуг остовного дерева положить равными 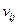, то для любой дуги 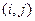, не принадлежащей дереву, будет справедливо соотношение

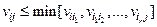, (п1.3)

где 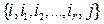- связная последовательность узлов дерева, принадлежащих пути из 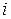в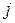. Из неравенств (п1.1) и (п1.2) получаем, что для любой дуги, не принадлежащей дереву,

. (п1.4)

Максимальное остовное дерево, удовлетворяющее равенству (п1.4), называется деревом разрезов потому, что каждая его ветвь соответствует разрезу, а вес ветви равен пропускной способности разреза. Если требуется определить величину максимального потока между двумя произвольными узлами, надо в дереве найти путь, соединяющий эти два узла, и выбрать в этом пути дугу с минимальным весом. Вес этой дуги равен величине потока между рассматриваемыми узлами.

Дата добавления: 2014-01-07