Анализ алгоритма Гаусса и его модификации

Запись алгоритма прямого хода.

Цикл по k = 1, 2,… n – 1.

1. Поиск строки с ненулевым ведущим элементом а_{m k} ¹ 0. Если такого элемента нет, то система не имеет решений. СТОП. Иначе поменять местами m -ю и k -ю строки.

2. Нормировка k -й строки:

a0:=a[k, k]; для j = k,…, n +1 вычислить a[k, j]:= a[k, j]/a0.

3. Преобразование строк с номерами i = k + 1,…, n:

a1:=a[i, k]; для j = k,…, n +1 вычислить a[i, j]:= a[i, j]*a1.

Конец цикла по k.

Конец прямого хода.

Текст программы данного варианта метода Гаусса приведен в Приложении 1.

Существование решения. Исходя из самого алгоритма, можно сделать вывод, что необходимым и достаточным условием существования решения задачи является наличие на каждом шаге прямого хода ненулевого ведущего элемента .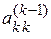

Оценка вычислительной сложности. Т.к. при прямом ходе используется тройной цикл, а при обратном – двойной, то вычислительная сложность алгоритма – О (n ³).

Анализ устойчивости. Определим влияние погрешностей округления на точность решения. Рассмотрим пример.

Пример 2.1. Дана система уравнений:

,

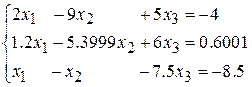решение которой, как легко проверить, равно x ₁ = 0, x ₂ = 1, x ₃ = 1.

Применим к этой системе метод Гаусса, в предположении, что все вычисления проводятся с точностью 6 значащих цифр (т.е. на 6-разрядной десятичной ЭВМ).

1 шаг. Исключаем из 2-го и 3-го уравнений x ₁. Получаем систему:

.

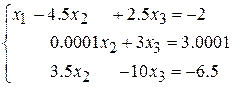2 шаг. Нормируем 2-е уравнение: x ₂ + 30000 × x ₃ = 30001, умножаем его на -3.5 и складываем с 3-м уравнением. В результате должно получиться

- коэффициент при x ₃: – 10 – 3.5×30000 = – 105010;

- свободный член: –6.5 – 3.5×30001 = – 105010.

Но за счет ошибок округления получим:

– 3.5×30001 = – 105003.5» – 105004.

Здесь число 105003.5, содержащее 7 цифр, округлилось до 6 значащих цифр. Далее, аналогично

–6.5 – 105004 = – 105010.5» – 105011.

Таким образом, после прямого хода получим следующую систему:

.

Обратный ход. .

x ₂ = 30001 – 30000 x ₃» 0.7; x ₁ = –2 – 2.5 x ₃ + 4.5 x ₂» – 1.35003.

Как видим, получился ответ, не имеющий ничего общего с точным решением.

Причина такой большой ошибки заключается в появлении больших коэффициентов, при округлении которых получена большая абсолютная ошибка D ~ 0.5. А большие коэффициенты появились после деления на маленький ведущий элемент .

Вывод. Для уменьшения влияния ошибок округления надо выбирать ведущий элемент не просто отличный от 0, но и достаточно большой.

Первая модификация метода. Назовем её поиск по строкам. Суть этого варианта алгоритма состоит в том, что элемент a_{m k} выбирается из условия .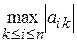

Если использовать этот способ для решения задачи примера 1.1, то на втором шаге ведущим будет элемент . Поменяем местами 3 и 2 строки и пронормируем полученную 2-ю строку. Получим после округления:

x ₂ – 2.85714 x ₃ = – 1.85714.

Умножим эту строку на –0.0001 и сложим с 3-й строкой (бывшей второй). В результате получим систему:

.

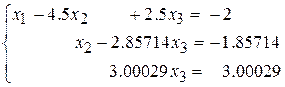При обратном ходе получим точное решение.

Вторая модификация метода. Назовем её поиск по столбцам. Недостаток первой модификации состоит в следующем. Предположим, какой-то x_i найден с погрешностью (при новой модификации погрешность уменьшается, но не исчезает). Если при нахождении какого-то x_s надо умножать x_i на большой коэффициент, | a_{s i} | >>1, то эта погрешность возрастет.

Вывод. Надо обеспечить, чтобы ведущий элемент был не просто большим, а максимальным по модулю в ведущей строке. Тогда при нормировке все прочие элементы строки будут меньше 1, и погрешности будут уменьшаться. Это можно обеспечить, если неизвестные x_i исключать в произвольном порядке. В каждой ведущей строке ищем 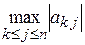– соответствующий элемент a_{k r} и будет очередным ведущим. После нахождения ведущего элемента надо будет поменять местами k - й и r -й столбцы.

Внимание. После такого обмена поменяется и нумерация неизвестных. Поэтому надо ввести целочисленный массив р ₁, …, р_n, элементами которого будут новые номера x_i после обмена. В начале прямого хода р_i = i. После нахождения ведущего элемента a_{k r} надо поменять местами p_k и p_r. При обратном ходе по формулам (2.7) вычисляются перенумерованные неизвестные x_i. После их вычисления надо положить

y[ p[i] ]:= x[i].

Набор y[1],…, y[n] и будет окончательным решением.

Третья модификация метода. Назовем её поиск по матрице. В качестве очередного ведущего элемента выбирается 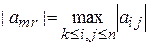, т.е. максимальный элемент во всей оставшейся части матрицы системы. После нахождения ведущего элемента надо менять местами k -ю и m -ю строки и одновременно k -й и r -й столбцы. Это вариант наиболее сложный для программирования, но и наиболее точный.

Дата добавления: 2014-01-07