Конечно-разностные формы уравнений Навье-Стокса и Рейнольдса

Расчет гидромеханических процессов.

Дифференциальные уравнения движения вязкой жидкости (уравнения Навье-Стокса)

До сих пор мы не рассматривали влияние сил вязкого трения на движение жидкости. Попытаемся учесть эти силы. Для простоты рассмотрим движение реальной (вязкой) жидкости в проекции на одну координату. Будем считать, что частица в форме параллелепипеда с размерами dx, dy, dz движется вдоль

оси X. За счёт сил вязкого трения на верхнюю и нижнюю поверхности рассматриваемого объёма будут действовать силы трения dT_в и dT_н соответственно. Эти силы зависят от площади трения dydz и величины касательного напряжения на поверхностях трения τ. На нижней поверхности сила трения будет:

,

на верхней она будет отличаться на величину приращения касательных напряжение вдоль оси Z

.

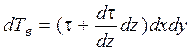Равнодействующая этих сил, действующая на рассматриваемый объём будет равна разности сил трения

,

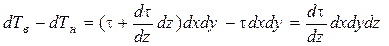или

,

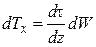где - величина рассматриваемого объёма жидкости.

Напряжение внутреннего трения, обусловленного вязкостью, по закону жидкостного трения имеет вид:

,

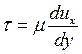где 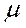- динамический коэффициент вязкости.

После подстановки получим:

.

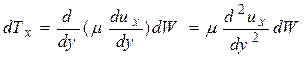В уравнениях Эйлера все силы отнесены к единичной массе, поэтому и силы, обусловленные вязким трением, приведём к такому же виду:

,

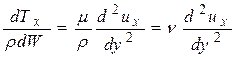где 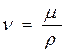- кинематический коэффициент вязкости.

Если подобные рассуждения провести для остальных координат, т.е. перейти к общему случаю пространственного движения, когда составляющие скорости 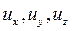являются функциями трёх координат X, Y, Z. В таком случае проекция силы вязкого трения на ось X в пересчёте к единице массы даёт величину:

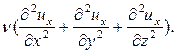
Аналогичные выражения можно записать для двух других координат. Если уравнения Эйлера для движущейся жидкости дополнить проекциями сил вязкого трения на оси координат, получатся дифференциальные уравнения движения вязкой жидкости, которые носят название уравнения Навье-Стокса и имеют следующий вид:

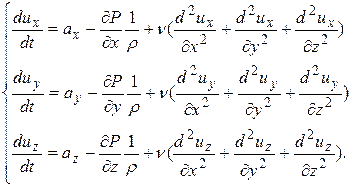
Общая схема применения численных методов и их реализация на ЭВМ.

Уравнение Навье-Стокса, как и уравнение Эйлера, интегрируются только для некоторых частных случаев, но в последние годы, в связи с развитием различных методов решения подобных задач, полученные уравнения используются все чаще и являются идеальным инструментом, позволяющим получить хороший результат. Наиболее часто для решения уравнений Навье-Стокса применяются численные методы.

На практике найти точное решение данного уравнения довольно сложно, так как искомое решение обычно не выражается в привычных для нас элементарных функциях. С появлением ЭВМ у исследователей появилась возможность решать подобные задачи численными методами. Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и логическим действиям над числами, т.е. к тем действиям, которые выполняет ЭВМ. В зависимости от сложности задачи, заданной точности и т.д. может потребоваться выполнить от нескольких десятков до многих миллиардов действий. В первом случае для получения решения достаточно иметь калькулятор, во втором – потребуется мощная ЭВМ, особенно, если необходимо получить решение в сжатые сроки.

Решение, полученное численным методом, обычно является приближенным, т.е. содержит некоторую погрешность. Источниками погрешности являются: 1) несоответствие математической задачи изучаемому реальному явлению; 2) погрешность исходных данных: 3) погрешность метода решения; 4) ошибки округлений в арифметических и других действиях над числами.

Погрешность в решении, обусловленная первыми двумя источниками называется неустранимой. Эта погрешность может присутствовать, даже если решение поставленной математической задачи найдено точно. Вопрос о том, насколько хорошо описывает математическая модель исследуемое явление, проверяется путем сравнения результатов. Влияние погрешности исходных данных часто удается оценить, применяя различные методы: наименьших квадратов, метод Лагранжа и др.

Численные методы в большинстве случаев сами по себе являются приближенными. Такие погрешности называются погрешностями метода. Это происходит потому, что численным методом решается более простая задача, аппроксимирующая исходную задачу. В ряде случаев используемый численный метод строится на базе бесконечного процесса, который в пределе приводит к искомому решению. Однако процесс вычисления всегда прерывается на некотором шаге, что дает приближенное решение.

При решении задач на ЭВМ чаще всего встречаются две ситуации:

1) если количество выполняемых арифметических действий невелико, то, обычно, ошибки округления не проявляются, так как в ЭВМ числа представляются с 10 и более десятичными значащими цифрами, а окончательный результат редко бывает нужен более чем с 5 десятичными значащими цифрами.

2) если задача сложная (уравнения с частными производными), то в этом случае погрешности округления в каждом действии не учитываются, так как они взаимокомпенсируются.

Для решения одной и той же задачи могут применяться различные приближенные методы, в зависимости от требуемой точности вычисления. Численный метод может считаться удачно выбранным, если его погрешность в несколько раз меньше неустранимой погрешности, а погрешность, возникающая за счет округлений, называемая вычисленной погрешностью, в несколько раз меньше погрешности метода. Если неустранимая погрешность отсутствует, то погрешность метода должна быть несколько меньше заданной неточности.

К численному методу предъявляется еще ряд других требований. Предпочтение отдается методу, который реализуется с помощью меньшего числа действий, требует меньшей памяти ЭВМ, является логически более простым, что способствует более быстрой его реализации на ЭВМ.

Большинство численных методов основано на замене более сложных объектов, уравнений более простыми. Наиболее удобной в обращении на практике функцией является алгебраический многочлен. Чтобы задать многочлен, нужно задать только конечное число его коэффициентов. Значения многочлена просто вычисляются, его легко продифференцировать, проинтегрировать и т.д. Алгебраические многочлены нашли широкое применение для приближения функций. Применяются многочлены четырех видов: Тейлора, интерполяционные, равномерного приближения, наилучшего среднеквадратичного приближения (метод наименьших квадратов).

Для интегрирования дифференциальных уравнений, которые не выражаются элементарными функциями, используются различные методы: Рунге-Кутта, Монте-Карло, Эйлера, Гауса и др. Нелинейные уравнения решаются методом итераций, деления отрезка пополам и др.

Существует большое число задач, где есть хорошо отработанные численные методы и созданные на их основе стандартные программы решения задач. Существует библиотека таких программ. Исследователь, которому впервые встретилась единичная задача, как правило, вначале ищет стандартную похожую программу, а затем пытается внести в нее изменения, исходя из имеющихся условий.

На первоначальном этапе исследования обычно используют более простую модель явления, которая позволяет воспользоваться более простыми методами решения с применением стандартных программ. Затем постепенно переходят к более сложным методам и моделям, добиваясь положительного конечного результата.

Наиболее широко численные методы используются в вычислительных экспериментах – исследовании естественнонаучных проблем, средствами вычислительной математики.

Математическому исследованию предшествует выбор физического приближения, т.е. решение вопросов о том, какие факторы надо учесть, а какими можно пренебречь. Далее проводится исследование проблемы методом вычислительного эксперимента, в котором выделяют несколько этапов:

1. Формируется задача, выбирается физическая модель процесса, решается вопрос о том, какие физические величины надо учитывать. Проводится описание физической модели математическим способом (дифференциальные, интегральные и другие уравнения). Полученную математическую модель исследуют методами математической физики, чтобы установить, правильно ли поставлена задача, хватает ли исходных данных, не противоречат ли они друг другу, существует ли решение поставленной задачи и единственно ли оно.

2. Построение приближенного численного метода решения задачи, т.е. выбора вычислительного алгоритма. Вычислительный алгоритм – последовательность арифметических и логических операций, при помощи которых находится приближенное численное решение математической задачи, сформулированной на первом этапе.

3. Программирование вычислительного алгоритма на ЭВМ.

4. Проведение расчетов на ЭВМ.

5. Анализ полученных численных результатов и последующее уточнение математической модели.

Дата добавления: 2014-01-07