Функции алгебры логики

Бовда Н. Д.

ДИСКРЕТНая МАТЕМАТИКа. Курс лекций. Часть II: учебное пособие / ВолгГТУ – Волгоград, 2006г. – 91 с.

ISBN 5-230-

Содержит теоретические сведения по темам: «Алгебра двузначной логики» и «Минимизация булевых функций».

Предназначено для студентов 1-го курса направления 552800 «Информатика и вычислительная техника», изучающих курс «Дискретная математика».

Библиография - 10 назв.

Табл. – 37

Печатается по решению редакционно-издательского совета Волгоградского государственного технического университета

ISBN 5-230-

©Волгоградский

государственный

технический

университет, 2006

ОГЛАВЛЕНИЕ

Глава 1. Алгебра двузначной логики. 5

§ 1.1. Функции алгебры логики. 5

§ 1.2. Способы задания функций алгебры логики. 8

§ 1.3. Таблицы истинности и элементарные функции. 8

§ 1.4. Эквивалентность функций. 11

§ 1.5. Реализация функций формулами. 13

§ 1.6. Эквивалентность формул и тождества. 17

§ 1.7. Упрощение формул. 18

§ 1.8. Двойственные функции и принцип двойственности. 21

§ 1.9. Применение принципа двойственности. 23

§ 1.10. Аналитическая запись функций алгебры логики. 24

§ 1.11. Аналитическое построение СДНФ и СКНФ.. 27

§ 1.12. Теорема о тройке связок. 29

§ 1.13. Полные системы функций и полиномы Жегалкина. 31

§ 1.14. Замыкание систем функций алгебры логики. 36

§ 1.15. Важнейшие замкнутые классы.. 37

§ 1.16. Теорема Поста о полноте. 45

Глава 2. Минимизация булевых функций. 48

§ 2.1. Основные понятия. 48

§ 2.2. Метод неопределенных коэффициентов. 51

§ 2.3. Тупиковые ДНФ и алгоритм наискорейшего спуска. 54

§ 2.4. Геометрическое представление функций алгебры логики. 59

§ 2.5. Аналитическое построение сокращенной ДНФ.. 63

§ 2.6. Локальные алгоритмы.. 65

§ 2.7. Алгоритм Куайна. 66

§ 2.8. Диаграммы Вейча–Карно. 69

§ 2.9. Построение ДНФ по карте Карно. 74

Задачи и упражнения. 79

Список литературы.. 90

Глава 1. Алгебра двузначной логики

Алгебра логики возникла в середине 19 века в трудах английского математика и логика Джорджа Буля. Её создание обусловлено стремлением разработать математический аппарат для решения традиционных логических задач, в которых требуется выяснить истинность или ложность тех или иных высказываний или правильность умозаключений. В настоящее время алгебра логики применяется для описания работы дискретных управляющих систем, таких, как контактные схемы, схемы из функциональных элементов, логические сети и др.. Интерес к алгебре логики, связанный с развитием вычислительной техники, привел к многим новым достижениям в этой науке.

Под высказыванием в алгебре логики понимают любое предложение, которое может быть оценено как «истинное» или «ложное». Сопоставим значению «истина» символ «1», а значению «ложь» – символ «0». Таким образом, алгебра логики оперирует на множестве всех высказываний со значениями из двухэлементного множества Е ₂ ={0, 1}. Обозначим множество всех высказываний – U. Элементы множества U будем обозначать строчными латинскими буквами a, b, c,…, a ₁, b ₁, c ₁, a ₂, b ₂, c ₂,…. Произвольные высказывания, которые могут принимать любое значение из множества U, будем называть переменными высказываниями или пропозициональными переменными, и обозначать символами x, y, z, x ₁, y ₁, z ₁, x ₂, y ₂, z ₂,….

Операции, заданные на множестве U, соответствуют употребляемым в обычной речи логическим связкам: «и», «или», «если…,то», «эквивалентно», частица «не» и т.д.. Назовем их логическими операциями или элементарными функциями алгебры логики. Позже будут введены обозначения для этих операций, сейчас же подчеркнем их функциональную природу, которая обусловлена их однозначным определением.

Из нескольких высказываний с помощью логических связок можно составить новые, более сложные высказывания, которые в свою очередь могут быть либо истинными, либо ложными. Истинность таких составных высказываний естественно зависит от истинности составляющих их высказываний. И эта зависимость, в силу однозначной определенности логических операций, также имеет функциональный характер. Таким образом, составные высказывания можно рассматривать как функции от простых высказываний. Назовем их истинностными функциями. Итак, сигнатура алгебры логики построена – это множество всех истинностных функций (или логических операций). Обозначим это множество Р ₂.

Теперь формально, алгебра логики задается двумя множествами: U и Р ₂, где U – это множество всех высказываний, принимающих значения «истина» или «ложь», или любое другое множество, элементы которого могут принимать одно их двух значений или находиться в одном из двух состояний. Например, множество переключателей, каждый из которых может быть «включен» или «выключен», или множество электрических сигналов, поступающих на вход некоторого устройства, –«сигнал есть» или «сигнала нет» и т.п..

А множество Р ₂ – это множество всех таких функций, которые принимают «истинностные» значения 0 или 1, если аргументы их пробегают те же значения. Алгебра логики занимается изучением свойств этих функций.

Истинностные функции называют также функциями алгебры логики, или булевыми функциями, или переключательными функциями.

Если f (x ₁, x ₂,…, x_n) – истинностная функция от n аргументов, т.е. f (x ₁, x ₂,…, x_n)Î Р ₂, то она определяет отображение f: 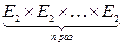® E ₂. Нетрудно подсчитать число всех таких отображений.

Теорема 1.1.1. Число всех функций алгебры логики от n переменных равно 2^{2 n}.

Доказательство: действительно, если x ₁, x ₂,…, x_n – пропозициональные переменные, то значение каждого x_i, где i =1,2,…, n, равно либо 0, либо 1. Каждый конкретный набор значений переменных x ₁, x ₂,…, x_n для краткости назовем «энкой». Каждую «энку» можно рассматривать как последовательность длины n, состоящую из нулей и единиц. Число всевозможных таких последовательностей длины n равно 2 ⁿ. Таким образом, значения каждой функции от n переменных определяются 2 ⁿ наборами – «энками». При этом для каждой «энки» эти значения могут быть равны 0 или 1. Тем самым, значения самой функции можно рассматривать как последовательность длины 2 ⁿ, состоящую из нулей и единиц. Различным функциям будут соответствовать различные последовательности длины 2 ⁿ, и каждая последовательность такой длины будет задавать некоторую функцию. Поэтому общее число различных функций от n переменных равно числу последовательностей длины 2 ⁿ из нулей и единиц и равно 2^{2 n}.

Функция, принимающая значение, равное нулю на всех «энках», называется «противоречием».

Функция, принимающая значение, равное единице на всех «энках», называется «тавтологией».

«Энки», на которых функция принимает значение, равное единице, называются единичными «энками» или единичными наборами.

«Энки», на которых функция принимает значение, равное нулю, называются нулевыми «энками» или нулевыми наборами.

§ 1.2. Способы задания функций алгебры логики

Укажем следующие 4 способа задания функций алгебры логики:

1) словесное описание;

2) табличное представление;

3) графическое изображение;

4) алгебраическое (в виде формулы).

Рассмотрим пример задания одной и той же функции от двух переменных каждым из перечисленных способов.

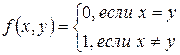– это словесное описание функции.

x	y	f (x, y)
			– табличное представление.

В графическом изображении единичные значения функции отмечаются некоторым способом, например «*», как на рисунке 1, а нулевые значения представляются неотмеченными вершинами единичного «куба» (в данном случае – квадрата).

Та же функция задается формулой: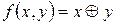

§ 1.3. Таблицы истинности и элементарные функции

Рассмотрим таблицу значений функции от n переменных. Число строк в такой таблице будет равно числу всевозможных «энок», т.е. равно 2 ⁿ. А число столбцов – числу переменных плюс единица, т.е. (n +1). При построении таблицы учтем, что каждую «энку» можно рассматривать как двоичное число, и выпишем их в порядке возрастания от 0 до 2 ⁿ –1.

Таблица 1

x 1	x 2	x 3	…	xn -1	xn	f (x 1, x 2, x 3,…, xn -1, xn)
			…			f (0,0,0,…,0,0)
			…			f (0,0,0,…,0,1)
			…			f (0,0,0,…,1,0)
…	…	…	…	…	…	……………
			…			f (1,1,1,…,1,1)

В правом столбце таблицы 1 выпишем значения функции на соответствующих «энках». Такая таблица называется таблицей истинности или комбинационной таблицей. Последнее название объясняется тем, что с помощью неё можно описывать поведение логических схем, называемых также комбинационными схемами или схемами без внутренней памяти, на вход которых подается n сигналов, а выход является функцией входного набора сигналов и полностью определяется этим набором.

Приведем примеры таблиц истинности для элементарных функций алгебры логики, к которым относятся функции от одной и от двух переменных.

Заметим, что число функций от одной переменной равно 4 (см. таблицу 2), а от двух переменных – 16 (см. таблицу 3).

Таблица 2

x	g 1(x)	g 2(x)	g 3(x)	g 4(x)

В таблице 2 функция g ₁(x) – это константа ноль или «противоречие».

Функция g ₂(x) – «тождественная функция x».

Функция g ₃(x) – «отрицание x», обозначается «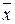» или «».

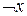Функция g ₄(x) – константа единица или «тавтология».

Таблица 3

x

y

f 1

f 2

f 3

f 4

f 5

f 6

f 7

f 8

f 9

f 10

f 11

f 12

f 13

f 14

f 15

f 16

Обозначение

&

x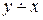

y

Å

Ú

¯

º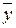

y ® x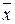

x ® y

|

В таблице 3 приведены обозначения элементарных функций. Эти обозначения (символы) принято называть пропозициональными связками или символами логических операций. Укажем также их названия, способы вычисления и прочтения.

Функция f ₁(x, y) – это так же, как и в таблице 2, константа ноль или «противоречие».

Функция f ₂(x, y)= x & y – «конъюнкция» х и у или «логическое умножение». Читается: «х и у». Значения этой функции можно получить простым умножением значений её аргументов или как наименьшее из значений аргументов, т.е. f ₂(x, y) = x & y = x×y = min (x, y).

Функции f ₃(x, y)= и f ₅(x, y)= 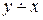– это «условное вычитание» у из х, и х из у, соответственно. Их значения можно получить по правилу: 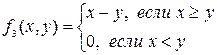и .

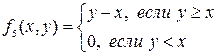Функции f ₄(x, y)= х и f ₆(x, y)= у – как и в таблице 2, «тождественная функция x» и «тождественная функция у» соответственно.

Функция f ₇(x, y)= х Å у – «сложение по модулю 2» или «исключающее или». Значения этой функции равны остатку от деления на 2 суммы её аргументов.

Функция f ₈(x, y)= х Ú у – «дизъюнкция» х и у или «логическое сложение». Читается: «х или у». Значения этой функции можно получить как наибольшее из значений аргументов, т.е. f ₂(x, y) = x Ú y = max (x, y).

Функция f ₉(x, y)= х ¯ у – «стрелка Пирса» или «отрицание дизъюнкции» или «конъюнкция отрицаний». Последние два названия обусловлены правилом, по которому получаются значения этой функции.

Функция f ₁₀(x, y)= х º у – «эквиваленция». Читается: «х эквивалентно у». Значения этой функции получаются по правилу: .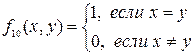

Функции f ₁₁(x, y)= 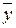и f ₁₃(x, y)= 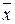– это так же, как и в таблице 2, «отрицание у» и «отрицание х» соответственно.

Функции f ₁₂(x, y)= y ® x и f ₁₄(x, y)= x ® y – это так называемая «импликация». Для чтения выражения x ® y можно использовать фразу «х влечет у» или «если х, то у». Значения x ® y получаются как ответ на вопрос «х меньше, либо равно у?». При этом положительный ответ записывается «1», а отрицательный – «0».

Функция f ₁₅(x, y)= y | x – «штрих Шеффера» или «отрицание конъюнкции» или «дизъюнкция отрицаний». Последние два названия обусловлены правилом, по которому получаются значения этой функции.

Последняя функция в таблице 3 – это так же, как и в таблице 2, константа единица или тавтология.

Дата добавления: 2014-01-07