Полные системы функций и полиномы Жегалкина

Обобщим результаты предыдущего параграфа.

Система функций алгебры логики F ={ f ₁, f ₂,…, f_s,…}Í P ₂ называется полной или функционально полной, если любая функция алгебры логики может быть записана в виде формулы через функции этой системы (или, как говорят, выражена формулой над F).

В соответствии с этим определением системы функций {Ø,&,Ú}, {Ø,&}, {Ø,Ú}, {Ø,®}, а также {¯} и {½} являются функционально полными.

Имеются ли другие полные системы функций? Этот вопрос можно решить с помощью следующей теоремы.

Теорема 1.13.1. О полных системах функций алгебры логики.

Пусть имеются две системы функций алгебры логики: F ={ f ₁, f ₂,…, f_p,…} и G ={ g ₁, g ₂,…, g_r,…}, относительно которых известно, что система F полна, и каждая её функция может быть выражена формулой через функции системы G. Тогда система функций G – является полной.

Доказательство:

Пусть h Î P ₂ – произвольная функция алгебры логики. В силу полноты системы F функцию h можно выразить формулой через функции системы F, т.е. h = S [ f ₁, f ₂,…, f_p,…]. А по условию теоремы каждую функцию из F можно выразить формулой через функции системы G, т.е. f ₁ = S ₁[ g ₁, g ₂,…, g_r,…], f ₂ = S ₂[ g ₁, g ₂,…, g_r,…],…. Поэтому в формуле для h можно исключить вхождения функций f ₁, f ₂,…, f_p,…, заменив их формулами над G. А именно, h = S [ f ₁, f ₂,…, f_p,…] = S [ S ₁[ g ₁, g ₂,…, g_r,…], S ₂[ g ₁, g ₂,…, g_r,…],…]= = S ¢[ g ₁, g ₂,…, g_r,…]. Таким образом, h выражена формулой через функции системы G. Но, поскольку h Î P ₂ – произвольная функция, то система функций G – является полной.

Используя эту теорему, покажем функциональную полноту следующих систем: (1) G ₁={º,Ú,0}, (2) G ₂={Å,&,º} и (3) G ₃={1,·,Å}, где «·» – это обычное умножение.

(1) Известно, что система функций {Ø,Ú} является полной. Поскольку «Ú» имеется в G ₁, а «Ø» выражается формулой 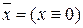, то G ₁ тоже полна.

(2) Известно, что система функций {Ø,&} является полной. Поскольку «&» имеется в G ₂, а «Ø» выражается формулой 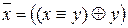, то G ₂ тоже полна.

(3) Т.к. система {Ø,&} является полной и х · у = х & у, а 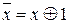, то G ₃ – полная система функций. Система G ₃ играет особую роль в алгебре логики, т.к. формула, сконструированная из функций {1,·,Å} и скобок, после раскрытия скобок и несложных алгебраических преобразований переходит в полином (сумму по модулю 2 элементарных произведений), называемый полиномом Жегалкина или совершенной полиномиальной нормальной формой (СПНФ).

Теорема 1.13.2. О представлении функции полиномом Жегалкина.

Каждая функция алгебры логики может быть выражена полиномом Жегалкина и причем единственным образом.

Доказательство:

Т.к. система функций {1,·,Å} является полной, то любая истинностная функция может быть выражена формулой через функции этой системы. Эта формула после преобразований, как уже указывалось в (3), переходит в полином Жегалкина. Таким образом, представление произвольной функции полиномом Жегалкина доказана. Докажем единственность этого представления. Для этого сначала запишем полином Жегалкина для произвольной функции от n переменных в общем виде: 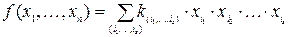, где s £ n и суммирование выполняется по модулю 2 и проводится по всевозможным подмножествам номеров переменных. А – коэффициент, равный нулю или единице, и стоящий перед произведением переменных с номерами: i ₁, i ₂,…, i_s. Число слагаемых в полиноме Жегалкина общего вида равно числу подмножеств из n –множества и равно 2 ⁿ. Полиномы Жегалкина различных функций от n переменных отличаются друг от друга наличием или присутствием тех или иных слагаемых, или, что то же самое, различным распределением значений коэффициентов в полиноме общего вида. Но, поскольку коэффициенты могут принимать лишь два значения, то число всех таких распределений равно , что совпадает с числом различных истинностных функций от n аргументов. Следовательно, для каждой функции имеется своё представление полиномом Жегалкина.

Примеры:

1) Построим полином Жегалкина для элементарной функции f (x, y) = х Ú у. Сначала запишем его в общем виде: f (x, y) =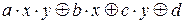. Где a, b, c и d – неопределенные коэффициенты, значения которых будут найдены путем подстановки различных комбинаций значений переменных х и у в выражение общего вида. Итак, f (0,0) = 0 =. Отсюда d =0.

f (0,1) = 1 =. Отсюда с =1.

f (1,0) = 1 =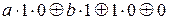. Отсюда b =1.

f (1,1) = 1 =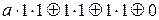. Отсюда a =1.

Тем самым, при подстановке найденных значений коэффициентов в выражение общего вида, получим: (х Ú у) =.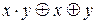

2) Построим полином Жегалкина для элементарной функции f (x, y) = х º у. Запишем выражение общего вида: f (x, y) =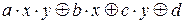и найдем коэффициенты: f (0,0) = 1 =. Отсюда d =1.

f (0,1) = 0 =. Отсюда с =1.

f (1,0) = 0 =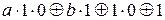. Отсюда b =1.

f (1,1) = 1 =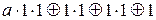. Отсюда a =0.

И полином Жегалкина: (х º у) = х Å у Å 1

Рассмотренный в примерах способ построения полинома Жегалкина представляет собой так называемый метод неопределенных коэффициентов.

Ввиду важности полиномиального разложения функций алгебры логики укажем и на другие способы получения этого разложения.

Если функция задана формулой со связками {Ø,&,Ú}, то для перехода к полиному Жегалкина необходимо воспользоваться тождествами: 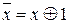, х & у = х · у, (х Ú у) =.

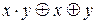Например, пусть f (x, y, z) = .

Тогда f (x, y, z) = ((x Å1)·(y Å1) Ú y) Ú (z Å1) = = ((x Å1)·(y Å1)· y Å (x Å1)·(y Å1) Å y) Ú (z Å1) =

=((x Å1)·(y Å1)· y Å (x Å1)·(y Å1) Å y)·(z Å1) Å ((x Å1)·(y Å1)· y Å (x Å1)·(y Å1) Å y)Å (z Å1) =((х · у Å x Å y Å1)· y Å х · у Å x Å y Å1Å y)·(z Å1) Å (х · у Å x Å y Å1)· y Å х · у Å x Å y Å1Å y Å z Å1 = (воспользуемся тем, что х · х = х и x Å х =0) = (х · у Å x Å1)·(z Å1) Å х · у Å x Å z = х · у · z Å х · z Å z Å х · у Å x Å 1Å х · у Å x Å z = = х · у · z Å х · z Å 1

Если функция задана таблицей, то для получения её полинома Жегалкина вначале следует записать СДНФ, затем в полученном выражении заменить все конъюнкции умножением, дизъюнкции – сложением по модулю два, а отрицания – сложением с единицей. Далее раскрыть скобки и применить тождества х · х = х и x Å х =0.

Например, пусть столбец значений функции f (x, y, z) в таблице истинности равен (1, 1, 1, 1, 1, 0, 1, 1). Запишем совершенную дизъюнктивную нормальную форму для этой функции: СДНФ(f (x, y, z)) = 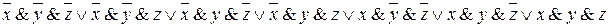. Теперь выполним указанные выше замены:

f (x, y, z)=(х Å1)(у Å1)(z Å1) Å (x Å1)(y Å1) z Å (x Å1) y (z Å1) Å (x Å1) yz Å x (y Å1)(z Å1) Å xy (z Å1) Å xyz, и раскроем скобки: (xyz Å xy Å xz Å yz Å x Å y Å z Å1) Å (xyz Å xz Å yz Å z) Å (xyz Å xy Å yz Å y)Å (xyz Å yz) Å (xyz Å xy Å xz Å x) Å (xyz Å xy) Å xyz = х · у · z Å х · z Å 1

Дата добавления: 2014-01-07