Метод неопределенных коэффициентов

Шаг 1. Для функции, заданной таблично, записывают ДНФ общего вида с неопределенными коэффициентами перед каждой элементарной конъюнкцией. Количество элементарных конъюнкций, а следовательно и неопределенных коэффициентов, определяется числом переменных функции и равно 3 ⁿ -1, где n – число переменных, и функция не равна тождественно единице. Таким образом, при n =3 их число составит 26, при n =4 оно равно 80. Поэтому этот метод реально применим для n £5 или 6, в виду быстрого роста числа неопределенных коэффициентов.

Шаг 2. Подставляя последовательно все наборы значений переменных в записанную ДНФ, получают 2 ⁿ уравнений относительно 3 ⁿ -1 неизвестных коэффициентов. В правой части каждого уравнения стоят значения функции на соответствующем наборе.

Шаг 3. Все коэффициенты уравнений, в правой части которых стоит 0, полагают известными, приравнивая их к нулю.

Шаг 4. В уравнениях с единицей в правой части вычеркивают слева все нулевые коэффициенты. Из оставшихся коэффициентов в каждом уравнении приравнивают к 1 тот коэффициент, который стоит перед конъюнкцией наименьшего ранга. Остальные коэффициенты полагают равными нулю. При этом в каждом уравнении должен быть выбран по крайней мере один единичный коэффициент и число таких коэффициентов по системе в целом должно быть минимальным.

Шаг 5. Подставляя все найденные единичные и нулевые коэффициенты в ДНФ общего вида, получают одну из МДНФ.

Другие МДНФ могут быть получены, если на 4-ом шаге имеется несколько вариантов выбора единичных коэффициентов. Комбинируя эти варианты, получим все МДНФ для данной функции.

Пример:

Пусть функция трех переменных f (x, y, z) задана таблицей 20:

Таблица 20

x	y	z	f (x, y, z)

В ДНФ общего вида такой функции будет 26 неопределенных коэффициентов. Для обозначения этих коэффициентов будем использовать букву k с нижним индексом, указывающим конъюнкцию, перед которой стоит этот коэффициент. С учетом всех принятых обозначений ДНФ общего вида запишется так:

1. ДНФ =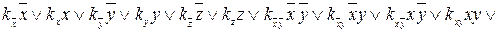

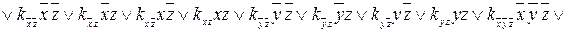
2. Теперь последовательно подставляя в ДНФ каждый набор значений переменных и приравнивая при этом получаемые выражения к значению функции на этом наборе, получим следующую систему уравнений:
ДНФ(0,0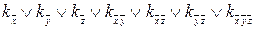,0): =0;
ДНФ(0,0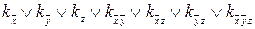,1): =1;
ДНФ(0,1,0): =1;
ДНФ(0,1,1): =1;
ДНФ(1,0,0): 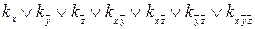=1;
ДНФ(1,0,1): =1;
ДНФ(1,1,0): =1;
ДНФ(1,1,1): 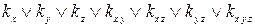=0;

3. Выполним шаг 3, приравнивая все коэффициенты первого и последнего уравнений к нулю.

4. Вычеркнув все нулевые коэффициенты в остальных уравнениях, получим новую систему уравнений, в которой число неизвестных меньше, чем в исходной, но все же превышает число самих уравнений:
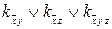=1;
=1;
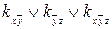=1;
=1;
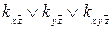=1;
=1;

В каждом уравнении полученной системы имеется по два коэффициента, которые могут быть приравнены к 1. Отсюда вытекает неоднозначность решения задачи. Учитывая то, что в каждом уравнении следует выбрать хотя бы один единичный коэффициент и общее число выбранных коэффициентов должно быть наименьшим, получим следующие два решения:

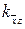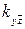Первое: =1; =1; =1;

Второе: 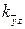=1; 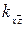=1; =1;

Остальные коэффициенты в обоих случаях приравниваем к нулю.

5. Подставляя найденные коэффициенты в исходную ДНФ, получим две минимальных ДНФ для заданной функции:

МДНФ₁ = и

МДНФ₂ = ;

Дата добавления: 2014-01-07