Локальные алгоритмы

Алгоритмы, устанавливающие свойства элементов множества и использующие на каждом шаге при этом только информацию об окрестности элемента, называются локальными.

Применение локальных алгоритмов к задаче минимизации булевых функций основано на понятии окрестности k –го порядка максимального интервала или соответствующей ему простой импликанты.

Под окрестностью нулевого порядка для некоторого максимального интервала N_Кi (или для элементарной конъюнкции К_i) функции f (x ₁, x ₂, …, x_n) понимают сам этот интервал (или саму эту конъюнкцию). Записывают этот факт так S ₀(N_Кi)={ N_Кi }.

Окрестность 1-го порядка интервала N_Кi представляет множество всех максимальных интервалов, имеющих непустое пересечение с S ₀(N_Кi), т.е. S ₁(N_Кi)={ S ₀(N_Кi), N_Кj,…, N_Кm }, где N_Кj ∩ S ₀(N_Кi)¹Æ,…, N_Кm ∩ S ₀(N_Кi)¹Æ. В терминах конъюнкций окрестность 1–го порядка простой импликанты К_i представляет собой множество тех простых импликант функции f (x ₁, x ₂, …, x_n), которые имеют общий множитель с конъюнкцией К_i, или являются близкими к ней.

Окрестность 2-го порядка для N_Кi – это множество интервалов, пересекающихся с окрестностью 1-го порядка хотя бы в одной вершине. А в терминах конъюнкций – это множество близких к К_i конъюнкций, а также конъюнкций, близких к последним. Аналогично можно определить окрестность порядка k для интервала N_Кi – это множество всех максимальных интервалов функции f, имеющих непустое пересечение с окрестностью порядка (k– 1) для N_Кi.

В локальных алгоритмах могут рассматриваться окрестности 1–го (алгоритм Куайна), 2–го (алгоритм регулярных точек) и k –го порядков (кольцевой алгоритм). Накопление информации об окрестностях простых импликант позволяет в дальнейшем проанализировать возможность удаления импликанты из СокрДНФ для получения минимальной ДНФ.

Рассмотрим построение окрестностей максимальных интервалов и простых импликант на примере.

Пусть функция трех переменных задана сокращенной ДНФ: . Это задание равносильно заданию функции сокращенным покрытием N_f: {(1,1,0),(1,1,1)}È{(1,0,0),(1,1,0)}È{(0,0,0),(1,0,0)}. Введем обозначения: К ₁= ху, К ₂=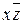, К ₃=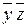и N_{К 1}= {(1,1,0),(1,1,1)}, N_{К 2}={(1,0,0),(1,1,0)}, N_{К 3}={(0,0,0),(1,0,0)}. Тогда окрестности нулевого порядка для каждой простой импликанты и каждого максимального интервала совпадают с ними самими. Окрестность 1–го порядка импликанты К ₁ есть множество { К ₁, К ₂}, а максимального интервала N_{К 1}– соответственно S ₁(N_{К 1})= { N_{К 1}, N_{К 2}}.

S ₁(К ₂)= { К ₂, К ₁, К ₃}, S ₁(N_{К 2})= { N_{К 2}, N_{К 1}, N_{К 3}};

S ₁(К ₃)= { К ₃, К ₂}, S ₁(N_{К 2})= { N_{К 3}, N_{К 2}};

S ₂(К ₁)= { К ₁, К ₂, К ₃}, S ₂(N_{К 1})= { N_{К 1}, N_{К 2}, N_{К 3}};

S ₂(К ₂)= { К ₂, К ₁, К ₃}= S ₁(К ₂), S ₂(N_{К 2})= { N_{К 2}, N_{К 1}, N_{К 3}}= S ₁(N_{К 2});

S ₂(К ₃)= { К ₃, К ₂, К ₁}, S ₂(N_{К 3})= { N_{К 3}, N_{К 2}, N_{К 1}};

S ₃(К ₁)= { К ₁, К ₂, К ₃}= S ₂(К ₁), S ₃(N_{К 1})= { N_{К 1}, N_{К 2}, N_{К 3}}= S ₂(N_{К 1});

S ₃(К ₃)= { К ₃, К ₂, К ₁}= S ₂(К ₃), S ₃(N_{К 3})= { N_{К 3}, N_{К 2}, N_{К 1}}= S ₂(N_{К 3}). И далее все окрестности более высоких порядков совпадают с уже найденными.

Дата добавления: 2014-01-07