Взаимное расположение двух прямых на плоскости.Рассмотрим две прямые, задаваемы уравнениями и

Любая прямая на плоскости XOY представляется линейным уравнением вида. И наоборот, любое линейное уравнение вида описывает прямую на плоскости XOY.

Возможны следующие случаи взаимного расположения этих прямых: 1) прямые совпадают, 2) прямые параллельны, 3) прямые пересекаются в одной точке. Исследуем соотношение между коэффициентами уравнений прямых в каждом из перечисленных случаев.

В случае 1) оба уравнения, описывающие одну и ту же прямую, должны совпадать или отличаться коэффициентом, на который можно сократить.

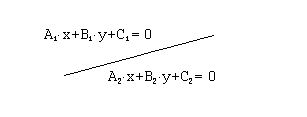
Таким образом, в данном случае .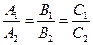

В случае 2) угловые коэффициенты обеих прямых одинаковы. То есть,

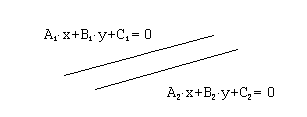
. Отсюда получим условие параллельности: .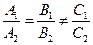

В случае 3) угловые коэффициенты прямых разные, то есть, 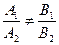, и

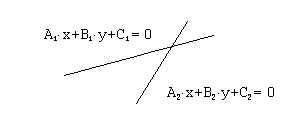
следовательно, прямые пересекаются в одной точке.

Точка пересечения двух прямых на плоскости находится решением системы уравнений

Кривые второго порядка. Кривой второго порядка называется кривая, описываемая уравнением второй степени, то есть уравнением, в которое переменные 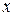и 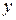входят с суммарной степенью не более 2. Таким образом, кривая второго порядка задается уравнением вида 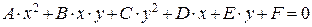. Обратное неверно: не любое уравнение второй степени задает реальную кривую. Так, если в уравнении

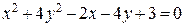выделить полные квадраты, мы получим уравнение , которому не может удовлетворить никакая точка из плоскости XOY с координатами .

Существуют три основных уравнения второй степени, задающие (с точностью до сдвига и поворота координатных осей) три основные кривые второго порядка: эллипс, гиперболу и параболу.

1. Эллипс. Каноническое уравнение эллипса, приведенное к координатным осям, имеет вид .

Эллипс пересекает ось OX в точках , а ось OY в точках 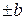. Нетрудно видеть, что вместе со значением уравнению удовлетворяет и 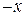, а вместе с 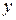и . Следовательно, эллипс – кривая, симметричная относительно осей координат.

Значения 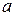и называются полуосями эллипса. В случае, когда полуоси равны, эллипс превращается в окружность .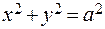

Как известно, окружность – геометрическое место точек, равноудаленных от точки, называемой центром окружности. Эллипс же – геометрическое место точек, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная. Фокусы эллипса, уравнение которого приведено выше, расположены на оси OX в точках 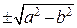, если 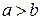, и на оси OY в точках 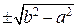, если .

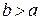Параметрическое задание эллипса: .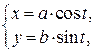

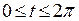2. Гипербола. Гиперболой называют геометрическое место точек, разность расстояний от которых до двух точек, называемых фокусами, есть величина постоянная. Каноническое уравнение гиперболы, приведенное к координатным осям, имеет вид 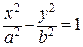, если фокусы гиперболы расположены на оси OX в точках 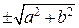. В этом случае гипербола пересекает ось OX в точках , а ось OY не пересекает.

В отличие от эллипса, расположенного в конечной части плоскости, гипербола – кривая, ветви которой уходят в бесконечность.

В том случае, когда фокусы гиперболы расположены в точках 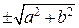на оси OY, гипербола задается каноническим уравнением 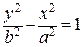, она пересекает ось OY в точках 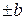и не пересекает ось OX.

Параметрическое задание гиперболы, пересекающей ось OX:

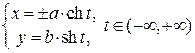. Параметрическое задание гиперболы, пересекающей ось OY: .

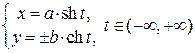Здесь функци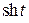и и – гиперболические синус и косинус, соответственно, имеющие представление 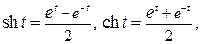и удовлетворяющие соотношению .

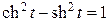3. Парабола. Каноническое уравнение параболы с вершиной в начале координат и осью симметрии OY имеет вид . В случае парабола расположена в верхней полуплоскости, в случае 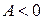– в нижней полуплоскости.

Уравнение параболы с осью симметрии OX имеет вид .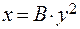

В качестве параметрического задания можно взять 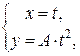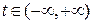, в первом случае и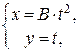 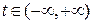, во втором случае. То есть роль параметра играет одна из декартовых координат.

Любое уравнение вида 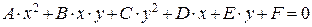,если оно имеет смысл, приводится путем линейной замены переменных вида 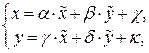к уравнению одного из трех перечисленных типов относительно 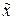и 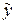. Указанная линейная замена переменных означает сдвиг, растяжение и поворот новых декартовых координатных осей относительно старых.

Дата добавления: 2014-01-07