Частные производные

Частной производной поx функцииz = f (x, y) в точкеM ₀(x ₀, y ₀) называется предел

,

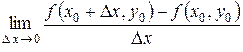если этот предел существует. Обозначается эта частная производная любым из следующих символов:

;;.

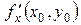Частная производная по x есть обычная производная от функции z = f (x, y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.

Совершенно аналогично можно определить частную производную по y функции z = f (x, y) в точкеM ₀(x ₀, y ₀):

=.

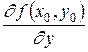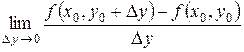В пространстве XYZ условие y = y ₀ описывает плоскость P, перпендикулярную оси OY и пересекающую эту ось в точке y ₀. Плоскость P пересекается с графиком функции z = f (x, y), вдоль некоторой линии L, как показано на рисунке 1. Тангенс угла между плоскостью XOY и касательной к линии L в точке с координатами x ₀, y ₀ равен частной производной по x функции z = f (x, y)в этой точке. В этом состоит геометрический смысл частной производной.

Аналогичное заключение можно сделать относительно частной производной по y.

Приведем примеры вычисления частных производных. Как говорилось выше, для вычисления частной производной по x функции z = f (x, y) нужно положить переменную y равной константе, а при нахождении частной производной по y нужно считать константой переменную x.

Примеры. 1. .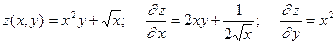

2.

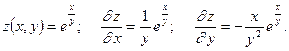
Если частные производные функции z = f (x, y) существуют на некотором множестве, а точка, в которой вычисляются частные производные несущественна, то пользуются более короткими обозначениями:

.

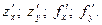Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные производные по x и по y. Они называются вторыми частными производными или частными производными второго порядка и обозначаются z_xx ¢¢, z_yy¢¢, z_xy¢¢ или 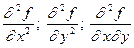. Согласно определению 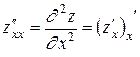; 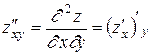. Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная z_xy¢¢ = (z_x¢) _y¢ может не быть равной z_yx¢¢ = (z_y¢) _x¢. Однако существует теорема, утверждающая, что если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности вычислялись частные производные по x и по y.

Пример. Рассмотрим функцию 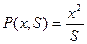, где x — численность в городах, S — расстояние между городами, P — пассажиропоток. Тогда 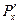— при одном и том же расстоянии между городами увеличение потока пассажиров пропорционально удвоенному числу жителей: 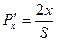; 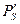— при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами: .

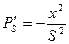Дата добавления: 2014-01-07