Связь криволинейного интеграла второго рода по замкнутой кривой в пространстве с поверхностным интегралом. Формула Стокса

Пусть C – гладкая замкнутая пространственная кривая, S – такая двусторонняя поверхность, что кривая C является границей этой поверхности. Тогда справедлива формула Стокса

, (ФС)

где выбор стороны поверхности, а значит, выбор знаков направляющих косинусов нормали к поверхности определяется заданием обхода по кривой C следующим образом: если глядеть с конца вектора нормали к поверхности C, должно быть видно, что обход кривой C совершается против часовой стрелки.

Следует пояснить, что собой представляет правая часть формулы Стокса. Под интегралом находится определитель, в верхней строке которого расположены направляющие косинусы вектора нормали к поверхности S, в средней строке расположены символические операторы нахождения частных производных, и в нижней строке расположены функции, представленные в криволинейном интеграле. Раскладывая определитель по верхней строке, мы получим поверхностный интеграл второго рода. Формальное «умножение» символического оператора на функцию означает, что от этой функции следует взять частную производную по соответствующей переменной.

Приведем другое представление правой части формулы Стокса в виде поверхностного интеграла второго рода по координатам:

.

Нетрудно заметить, что в том случае, когда кривая C расположена в плоскости XOY, и в качестве S мы выберем плоскую область, ограниченную кривой C, формула Стокса превращается в уже известную формулу Грина.

Для доказательства параметризуем поверхность S:

, . Будем считать функции дважды непрерывно дифференцируемыми в области значений параметров . Таким образом, благодаря параметризации мы перешли от поверхности S к области , находящейся в параметрической плоскости. Граница C поверхности S соответствует границе области , которую мы назовем . Посчитаем первое слагаемое в криволинейном интеграле с применением введенной параметризации и формулы Грина для интеграла по замкнутой кривой в параметрической плоскости.

Аналогично доказывается, что 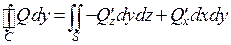и .

Сложив все левые и все правые части полученных соотношений, мы получим формулу Стокса.

Благодаря формуле Грина мы получали условие независимости криволинейного интеграла на плоскости от пути интегрирования. Подобным образом, применяя формулу Стокса, можно получить условия независимости криволинейного интеграла в трехмерном пространстве от пути интегрирования. Эти условия имеют вид: .

Дата добавления: 2014-01-07