Операция интегрирования

Оператор взятия неопределенного интеграла – также является оператором линейным.

Свойство некоего объекта быть «дифференцирующим» (иногда – «разностным») или «интегрирующим» (иногда – «суммирующим») часто задаются как функции неких черных ящиков, которые выполняют в системе некие управляющие функции.

4. Процессы "без памяти" – марковские процессы.

Рассмотрим систему. Пусть она может быть в некотором количестве разных состояний. Пусть вследствие каких-то причин – либо внутреннего, либо внешнего происхождения – система будет переходить из одного состояния в другое.

Такие переходы могут быть двух родов. Переходы первого рода – когда система из состояния 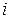переходит в состояние 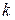: 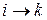, и притом такой переход осуществляется всегда. Таким образом, процессы в системе – для этого класса случаев – могут быть заданы как цепочка сменяющих друг друга состояний.

Но может быть и другой случай: система осуществляет переход 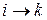в вероятностном смысле. Другими словами, конечное состояние системы уже не фиксировано, и для следующего состояния системы открыты, в общем случае, все состояния (включая и вероятность – возможность – остаться в прежнем).

Для практических приложений важное значение имеет случай, когда вероятности перехода системы в иное состояние зависят только от текущего ее состояния, – то есть от того состояния, в котором она находится в настоящий момент, но не от того, в каких состояниях она находилась ранее.

Именно такие случаи имеют место во многих экономических ситуациях. Совершенно безразлично, какие достижения имела фирма ранее: инвесторов, интересует ее прогноз на будущее – а он определяется только ее настоящим положением на рынке.

Случайные процессы могут служить достаточно мощным аппаратом для моделирования динамики, смены состояний и перспектив развития в социальных и экономических системах. Существуют разные способы рассмотрения такой случайности. Например, случайность может быть «введена» на уровне модели исследуемой системы посредством того, что переходы между состояниями системы осуществляются в случайные моменты времени. Или же – сами переходы являются случайными, – например, существует вероятность перехода в несколько разных состояний. В общем же случае – может быть все: и случайные моменты времени, и случайные переходы между состояниями, да и сами вероятности таких переходов могут быть случайными – например, когда они происходят под воздействием случайных изменений во внешней по отношению к исследуемой системе среде. Заметим, что в последнем случае мы приходим к модели описания взаимодействия изучаемой системы с внешней средой.

Определение:Случайный процесс является марковским, когда любая дополнительная информация, кроме знания ее текущего состояния 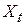, является несущественной для осуществления прогноза дальнейшей смены состояний системы.

Идея подхода к моделированию социальных и экономических систем с помощью стохастических дифференциальных уравнений состоит в том, что взаимодействие системы с внешним окружением полагается изменяющимся случайным образом. В этом случае приращение состояния системы 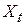задается формулой:

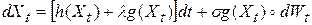. (14)

Здесь полагается, что взаимодействие между исследуемой системой и внешней средой описывается при помощи случайного процесса

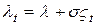, (15)

где 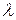задается неким усредненным состоянием окружающей среды, а изменяющаяся случайная добавка – «шум» – имеет нулевое среднее значение и дисперсию, равную s².

В (14) первый член является дифференциальным уравнением, описывающим эволюцию системы, а второй – описывает случайные добавки в это дифференциальное уравнение.

5. Уравнение Колмогорова (Фоккера-Планка) и его статистическая интерпретация.

Текущее состояние исследуемой системы может быть описано только в рамках плотности вероятности 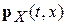для того, чтобы обнаружить систему в момент времени 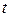в некоем состоянии 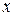(мы перешли к обозначению состояний маленькими буквами).

Зная вид уравнения (14) для эволюции состояния системы, необходимо найти эволюцию со временем плотности вероятности для системы иметь состояние 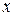в момент времени 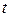. Из теории стохастических дифференциальных уравнений известно, что искомая плотность вероятности 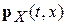может быть найдена как решение дифференциального уравнения в частных производных

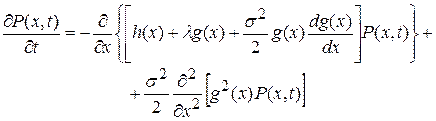. (16)

Уравнение (16) называется прямым уравнением Колмогорова, или чаще – особенно в англоязычной литературе – уравнением Фоккера-Планка. Отметим, что, в общем случае, могут быть разные интерпретации уравнения (14) – соответственно и разные уравнения Фоккера-Планка.

Для широкого класса уравнений вида (14) уравнение (16) допускает стационарное решение. Это означает, что для произвольного вида начальной плотности вероятности с течением времени устанавливается стационарная плотность вероятности, или, иными словами, имеет место асимптотический закон 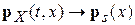при 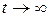. Пользуясь формулами (14) или (16) можно даже записать вид такой стационарной плотности вероятности. Она задается формулой

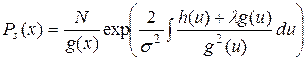. (17)

Здесь 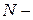нормировочный множитель, который находится по формуле

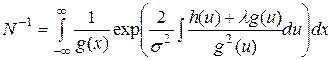. (18)

Если вычисленное значение, 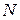конечно, то стационарная плотность вероятности существует и для ее вычисления имеет место формула (17). Таким образом, имеет место простой алгоритм действий: если имеется задача, задаваемая уравнением вида (14), то вычисляется для нее интеграл (18). Если он конечен – то задача допускает существование стационарной плотности вероятности, выражение для которой может быть вычислено по формуле (17).

Дата добавления: 2014-01-07