Салыстыру белгілері

4-теорема. Егер қатарлары мүшелері теңсіздігін қанағаттандырса, онда

1) қатары жинақты болса, онда 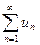қатары да жинақты;

2) 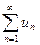қатары жинақсыз болса, онда 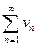қатары да жинақсыз;

3) Егер (1) және (2) қатарлар үшін онда екі қатар да жинақты, не екеуі де жинақсыз.

5-теорема (Даламбер белгісі). 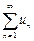, (1) болсын. Егер

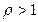а) болса, қатар жинақты; ә) болса, жинақсыз;

б) болса, белгісіз.

6-теорема (Коши белгісі). Теріс емес мүшелі , қатары беріліп, шегі бар болсын. Онда, егер

а) болса, қатар жинақты; ә) болса, жинақсыз;

б)болса, белгісіз.

7-теорема (Кошидің интегралдық белгісі)

, (1)

қатар мүшелері өспейтін болсын. Яғни,

(2)

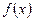функциясы өспейтін және 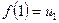, ,..., ... 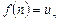болсын.

Онда, егер меншіксіз интегралы жинақты болса, онда (1) қатар да жинақты. Ал, егер меншіксіз интеграл жинақсыз болса, онда қатар да жинақсыз.

Қатар жинақтылығының Коши критерийі

8-теорема. 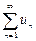, (1) қатар жинақты болуы үшін 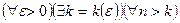және саны үшін (5)

теңсіздігінің орындалуы қажетті және жеткілікті.

(5)-ті келесідей жазуға да болады:

(5’).

Айнымалы таңбалы қатарлар.

Анықтама. (1)-қатарды айнымалы таңбалы қатар деп атайды, егер оның құрамындағы оң және теріс таңбалы мүшелерінің саны ақырсыз болса.

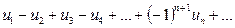, (2)

(2)-қатарды ауыспалы таңбалы қатар деп атайды. Ауыспалы таңбалы қатарайнымалы таңбалы қатардың дербес жағдайы.

9-теорема (Лейбниц белгісі). (2)-ші қатардың мүшелері келесі шарттарды қанағаттандырсын:

(3)

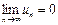(4)

Онда (2)-ші қатар жинақты. Оның қосындысы бірінші мүшесінен аспайды, .

1-ескерту. Егер (3)-шарт белгілі бір номерден бастап орындалғанда да теорема ақиқат.

2-ескерту. Егер ауыспалы таңбалы қатар Лейбниц теоремасының шарттарын қанағаттандырса, онда қатардың қосындысын оның қандай да бір дербес қосындысымен ауыстырғандағы дәлдікті анықтауға болады.

Мұндай ауыстыруда мүшеден бастап алынып тасталған қатар мүшелері де ауыспалы таңбалы қатар құрайтын болғандықтан ол қатардың қосындысы абсолют шамасы бойынша бірінші мүшесінің модулінен аспайды, яғни .

Абсолютті және шартты жинақтылық

Айнымалы таңбалы (1)-қатар мүшелерінің абсолют шамаларынан құрастырылған қатарды қарастырайық

(5)

10-теорема. Егер (5)-қатар жинақты болса, (1)-қатар да жинақты.

Ескерту. 10-теоремаға кері тұжырым дұрыс емес, яғни (1)-қатардың жинақтылығынан (5)- қатардың жинақтылығы шықпайды.

Анықтама. Егер айнымалы таңбалы қатар мүшелерінің абсолютті шамаларынан құралған (5)- қатар жинақты болса, онда айнымалы таңбалы (1)-қатарды абсолютті жинақты қатар деп атайды.

Анықтама. Егер айнымалы таңбалы (1)-қатар жинақты болып, ал оның мүшелерінің абсолют шамаларынан құралған (5)- қатар жинақсыз болса, онда айнымалы таңбалы қатарды шартты жинақты деп атайды.

11-теорема. 1)Егер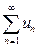, (1) абсолютті жинақты болса, онда қатары да абсолютті жинақты болады.

2) Егер және қатарлары абсолютті жинақты болса, онда қатары да абсолютті жинақты болады.

13- дәріс. Функционалдық қатарлар

Функциялық тізбектер мен қатарлар

функциялар тізбегі берілсін.

Анықтама. Егер үшін болса, онда функциялық тізбек Е (-ке) жиынында нүктелі жинақталады деп атайды.

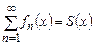– функциялдық қатар.

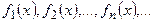функциялар тізбегіне қатысты келесідей сұрақтар туындайды.

1) 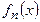, функциялары үзіліссіз болса, онда шегі болатын функция үзіліссіз бола ма?

2) 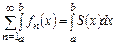орындала ма?

3) 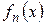–дифференциялданатын болса, 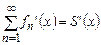орындала ма?

Бұлар әр уақытта орындалмайды. Ол үшін белгілі бір шарттардың орындалуы қажет.

Анықтама.

Бұл анықтамада әрбір 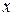үшін өзінің номері табылады. Мұндай жинақтылықты нүктелі жинақтылық деп атайды. Оны 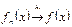символдарының бірімен белгілейді.

Барлық үшін ортақ табыла ма деген сұрақ туындайды.

Мысалы,1) , , ;

, ;

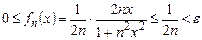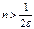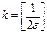, , . Табылады.

2) , ,

, , .

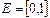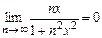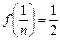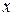Егер , , яғни болғанда кез келген -терге ортақ 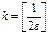номерлерін көрсете алмаймыз.

Анықтама (бірқалыпты жинақтылық).

Бұл анықтамада барлық 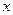үшін ортақ номері табылады. Осындай жинақтылықты бірқалыпты жинақтылық деп атайды. Оны , 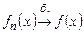символдарының бірімен белгілейді.

12-теорема. Е жиынында анықталған 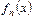функциялар тізбегі Е жиынында бірқалыпты жинақты болуы үшін

теңсіздігінің орындалуы қажетті және жеткілікті.

Функциялық қатарлардың бірқалыпты жинақтылығы

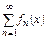, (1)

қатры берілсін. (1)- қатардың дербес қосындылары болсын.

Анықтама. (1)-қатарды Е жиынында бірқалыпты жинақты деп атайды, егер 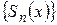дербес қосындыларының тізбегі Е жиынында -ке бірқалыпты жинақталса.

,

, . Осыдан .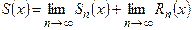

(1)- қатардың Е жиынында бірқалыпты жинақталуы эквивалентті.

14-теорема (қажетті шарт). (1)-қатар Е жиынында бірқалыпты жинақты болса, онда

15-теорема (Вейерштрасс белгісі). Е жиынында 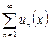, (1) 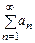, (2), қатарлары берілсін. Егер (2)-қатар жинақты болып, Е-ден алынған кез келген 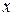-тер үшін болса, онда (1)-қатар Е жиыныда абсолютті және бірқалыпты жинақты болады.

Вейрштрасс теоремасы қатардың бірқалыпты жинақтылығы үшін қажетті емес, жеткілікті.

Ескерту. Бірқалыпты жинақты функциялық қатарды жақшалар қою арқылы Вейертрасс теоремасының шарты орындалатындай қатарға келтіруге болады.

Бірқалыпты жинақты қатарлардың қасиеттері

16-теорема (қатар қосындысының үзіліссіздігі). Егер үзіліссіз функцияларынан құралған (1)-қатары Е жиынында бірқалыпты жинақты болса, онда 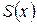те үзіліссіз болады.

17-теорема (мүшелеп интегралдау). Егер (1)-қатар мүшелері 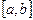аралығында үзіліссіз болып, қатар осы аралықта бірқалыпты жинақты болса, онда қатарды мүшелеп интегралдауға болады. Яғни,

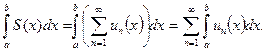
18-теорема (мүшелеп дифференциялдау). Егер (1)-функциялық қатардың мүшелері 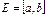аралығында:

1. Қатар мүшелерінің үзіліссіз туындылары бар;

2. (1)-қатар нүктелі жинақты, яғни ;

3. 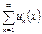–бірқалыпты жинақты болса, онда қатардымүшелеп дифференциялдауға болады. Яғни, .

Дәрежелік қатарлар. Жинақтылық радиусы

Анықтама. , (1) қатарды дәрежелік қатар деп атайды, мұндағы 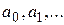–коэффециенттер.

19-теорема (Абель теоремасы). Егер (1)-қатар 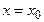нүктеде жинақты болса, онда 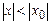барлық нүктелерде абсолют жинақты. Ал егер қатар нүктеде жинақсыз болса, онда ол барлық нүктелерде жинақсыз.

Егер (1)-қатар жинақты болатын болса, онда нақты саны табылып, барлық нүктеде қатар жинақты, ал бар нүктеде қатар жинақсыз.

Осыдағы - ді жинақтылық радиусы деп атайды.

Ал және болғанда қатарды жинақтылыққа осы мәндерді қою арқылы тексереміз.

Дәрежелік қатардыңжинақтылық радиусын анықтау үшін

қатарын қарастырайық. Даламбер белгісін қолдансақ онда,

Осы сияқты, жинақтылық радиусын – Коши – Адамар формуласы арқылы анықтауға болады.

20-теорема. (1)-қатар аралығында бірқалыпты жинақты.

1-салдар. 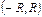жинақтылық интервалында (1)-қатардың қосындысы үзіліссіз.

2-салдар. Егер интегралдау шектері 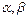жинақтылық интервалында жатса, онда 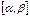аралығында дәрежелік қатарды мүшелеп интегралдауға болады. Яғни,

.

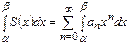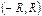3-салдар. Жинақтылық радиусы болатын дәрежелік қатардың қосындысы болса, онда интервалының әрбір нүктесінде дәрежелік қатарды мүшелеп дифференциалдауға болады. Яғни,

Дифференциалдағанда пайда болған қатардың жинақтылық радиусы алғашқы қатардың жинақтылық радиусына тең болады.

Мысалы.

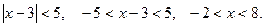
болса, ауыспалы таңбалы қатары, Лейбниц белгісі бойынша, жинақты.

болса, 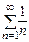- гормониялық қатар жинақсыз. Демек, 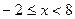мәндерінде қатар жинақты.

Тейлор қатары

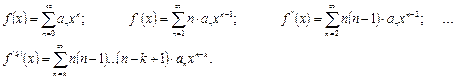
Егер болса, онда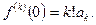

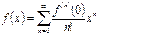
Дәрежелік қатар түрінде бейнеленетін функцияны аналитикалық функция деп атайды.

Аналитикалық функция ақырсыз рет дифференциялданады. Бірақ кері болмауы мүмкін. Ақырсыз рет дифференциялданатын функция аналитикалық болмауы мүмкін.

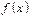функциясы аралығында анықталған нүктесінде ақырсыз рет дифференциялданатын болсын. Онда (6)-қатар - 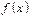-функциясының Тейлор қатары болады.

21-теорема. 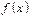функциясы 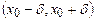аралығында ақырсыз рет дифференциялдансын. Егер қандай да бір

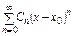, (7)

дәрежелік қатары әрбір 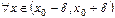үшін болса, онда бұл дәрежелік қатар 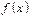-функциясының Тейлор қатары болады.

22-теорема. 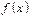функциясы және оның туындылары аралығында шенелген болса, яғни

(8)

болса, онда осы аралықта

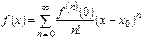. (9)

Дәрежелік қатардың қолданылуы

Мысалдар. 1)

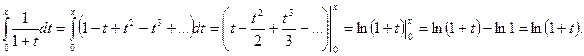
Демек, .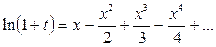

2)

3) .

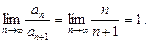
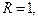
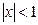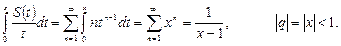
14-дәріс. Еселі интегралдар

Қос интегралдың анықтамасын енгізуден бұрын төбесі қисық цилиндрдің көлемін есептеу есебін қарастыралық, яғни цилиндрдің төбесінің теңдеуі 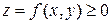екі айнымалы үзіліссіз функция болсын. Қисық төбелі цилиндрдің биктіктері өзгеріп отыратындықтан, оның қөлемін тегіс төбелі цилиндр көлемін есептеу формуласымен есептей алмаймыз. Алайда, біз қисық сызықты трапецияның ауданын есептегенде пайдаланған «бөлу, жуықтау, қосындылау, шек табу» арқылы біртіндеп қисық төбелі цилиндрдің көлемін есептейміз.

облысын кез келген әдіспен дана кішкентай тұйық , ,…, 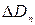облыстарға бөлеміз, кішкентай тұйық облыс - дің ауданын ( 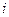= 1,2,…,) арқылы белгілейік, ал табаны болған жіңішке қисық төбелі цилиндрдің көлемі ( 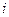= 1,2,…,) болсын, онда осы қисық төбелі цилиндрдің көлемі келесідей болады:

.

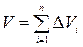тұйық облысынан кез-келген нүктесін алып, биіктігі 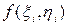болатын жіңішке тегіс төбелі цилиндрдің көлемі арқылы жіңішке қисық төбелі цилиндрдің көлемі - ді жуықтап табамыз, яғни:

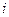≈ ( = 1,2,…,).

Сонымен, қисық төбелі цилиндрдің көлемі осы дана тегіс төбелі жіңішке цилиндрлердің көлемдерінің қосындысына жуықтайды, яғни:

≈,

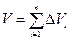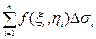әрбір кішкентай облыстың диаметрлерінің ең үлкенін λ арқылы белгілейік, егер 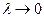кезде жоғарыдағы өрнектің оң жағындағы қосындының шегі бар болса, онда осы шек анықтамақ болып отырған қисық төбелі цилиндрдің көлеміне тең болады, яғни:

.

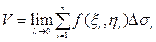Жоғарыда бір геометриялық есеп туралы айттық, онда анықтамақ болған шаманы бір қосындының шегі мәселесіне айналдырдық, бұдан тыс, басқада көптеген физикалық, геометриялық, экономикалық шамаларды да белгілі бір қосындының шегі мәселесіне айналдырып есептейміз.

Анықтама. Берілген функциясы шектелген түйық облысында анықталған болсын. облысын кез келген әдіспен п элементар бөлікке бөліп, оның әрқайсысының ауданын арқылы белгілейік.

Әрбір элементар облыстан нүктесін алып, көбейтіндісін анықтайық.

функциясының облысы бойынша иитегралдық қосындысы деп

өрнегін айтады.

облысы бойынша функциясының қос интегралы деп иитегралдық қосындының әрбір 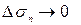ұмтылғандағы шегін айтады да былай белгілейді:

.

Егер функциясы тұйық облысында үзіліссіз болса, онда интегралдық қосындының шегі бар болады және ол облысын п бөлікке бөлуге және әр бөліктен алынған 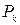нүктесіне байланысты болмайды.

Ескертулер. 1. функциясы шектелген тұйық облысында үзіліссіз болса, онда 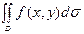қос интегралы бар болады.

2. Егер тік бұрышты координаталар жүйесінде координаталық остерге параллель болатын сызықтар торымен облысын бөлсек, онда аудан элементі - ны арқылы, ал қос интегралды 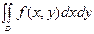арқылы жазуға болады.

Қос интегралдың қасиеттері.

облысы жазықтығындағы шектелген тұйық облыс, ал - ның ауданы болсын, онда келесі қасиеттер орындалады:

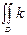
1⁰. 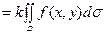, мұндағы 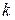- тұрақты сан;

2⁰. ;

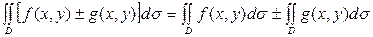3⁰. Егер интегралдау облысы - ны және екі бөлікке бөлсек, онда

;

4⁰. Егер 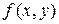функциясы облысында үзіліссіз болса, онда облысында ең болмағанда бір 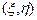нүктесі табылып, келесі теңдік орындалады:

.

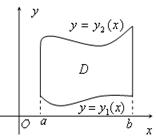
2. Тік бұрышты координаталар жүйесінде қос интегралды есептеу

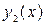
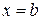
Берілген облысы осіне қарағанда дұрыс облыс болып , үзіліссіз қисықтармен және ,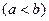түзулермен шектелсе, онда қос интеграл келесі екі еселі интеграл арқылы есептеледі:

. (7.1)

Үстіңгі жағынан үзіліссіз бетімен, астыңғы жағынан облысымен, бүйір жағынан жасаушылары 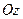осіне параллель, ал бағыттаушысы облысының контуры болып келген цилиндрлік дене көлемі формуласымен есептелінетіндігі белгілі болды, енді осы көлемді анықталған интегралға айналдырып есептейік.

аралығындағы кез-келген 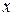арқылы өткен дененің қима бетінің ауданын 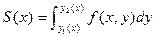формуласымен есептейміз, содан кейін қайтадан анықталған интегралды қолдану арқылы көлемді есептейміз, яғни

.

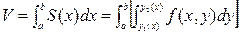
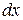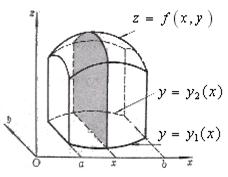
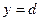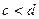облысы осіне қарағанда дұрыс облыс болып, төменнен және жоғарыдан және () түзулерімен, сол және оң жағынан 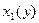, үзіліссіз қисықтармен шектелсе, онда қос интеграл келесі екі еселі интеграл арқылы есептеледі:

. (7.2)

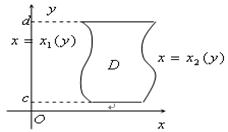
Егер облысы дұрыс облыс болмаса, онда оны дұрыс облыстарға бөлу қажет.

Ескертулер. 1. Жоғарыдағы екі еселі интегралдарда жоғарғы және төменгі шектерді белгілеу өте маңызды, бұл көбінесе облысын сызуды қажет етеді.

2. Жоғарыдағы екі түрлі интегралдау облыстарының екеуі де келесі шартты қанағаттандыруы керек, яғни, дұрыс облыс деп осы шартты қанағаттандыратын облысты айтамыз.

облысының ішкі бөлімінен өтетін әрі және өстеріне параллель болатын түзулер мен - ның шекарасының қиылысу нүктелері екеуден көп болмауы керек. Егер облысы ол шартты қанағаттандырмаса, онда - ны әрбір бөлігі аталған шартты қанағаттандыратындай бірнеше бөліктерге бөліп, сосын қос интегралдың жоғарыдағы 3⁰ - қасиетін пайдаланып есептейміз.

Мысалдар. 1. Интегралдау облысы : параболасымен және сызығымен қоршалған екі еселі интегралға келтіріңіз.

Шешуі. Берілген парабола мен түзу сызықтың қиылысу нүктесі және . Сонымен облысы суреттегідей болады.

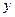
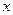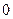
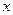
Оны ， арқылы белгілесек, онда формула бойынша

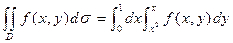болады.

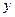
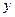
облысын ， түрінде де өрнектеуге болады. Ол кезде 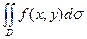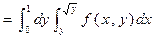болады.

Дата добавления: 2014-01-07