Лекція 4. Моделювання динаміки економічних процесів дискретних у часі

1.Скінченно-різницеві рівняння – основний математичний апарат аналізу економічних процесів дискретних у часі.

Більшість економіко-математичних моделей характеризується статичним підходом до вивчення економіки, коли її стан досліджується в заданий момент часу. Під статичною економічною системою розуміється така система, координати якої на досліджуваному відтинку часу можуть вважатися сталими. Відповідно, при формулюванні статичної економіко-математичної моделі припускається, що всі залежності відносяться до одного моменту часу, а система, що моделюється, є незмінною в часі. При цьому ігноруються можливі, а інколи неминучі зміни, оскільки їх врахування не вимагається поставленою метою моделювання. Крім того, припускається, що всі процеси, які протікають в системі, не вимагають для свого аналізу розгортання в часі, так як можуть бути з достатньою ступінню точності схарактеризовані незалежними від часу величинами. Тому в статичній моделі час не вводиться явно. Статичні моделі характеризують економічну систему на будь-якому фіксованому моменті часу. Оскільки статичні моделі у формалізованому вигляді не містять фактора часу, вони завжди простіші динамічних моделей тих самих економічних систем, які в тій чи іншій мірі враховують цей фактор.

Під динамічною системою розуміють всяку систему, яка змінюється в часі. Час в економічній динаміці може розглядатися як неперервний або дискретний. Неперервний час зручний для моделювання, так як дає змогу використати апарат диференціального числення і диференціальних рівнянь. Дискретний час зручний для розв’язування прикладних задач, оскільки статистичні дані завжди дискретні і відносяться до конкретних одиниць часу. Для дискретного часу використовують апарат різницевих рівнянь.

Математичний опис динамічних моделей здійснюється, як правило:

· системами диференціальних рівнянь, в яких неперервною змінною є час;

· різницевими рівняннями, де час – дискретна величина;

· системами звичайних алгебраїчних рівнянь.

За допомогою динамічних моделей, зокрема, розв’язуються задачі планування і прогнозування економічних процесів:

· визначення траєкторії розвитку економічної системи та її стан у задані моменти часу;

· аналіз економічної системи на стійкість;

· аналіз структурних зсувів.

У практичній діяльності використовується багатогалузеві динамічні моделі розвитку економіки, виробничі функції, теорії економічного зростання.

Диференціальні рівняння знаходять достатньо широке застосування в моделях динамічної економіки, в яких відображаються не лише залежність змінних від часу, але й їх взаємозв’язок у часі.

Аналіз динамічних систем і їх математичне моделювання базується на чисельних методах розв’язування систем диференціальних рівнянь. Особливе місце серед чисельних методів розв’язування динамічних моделей з дискретним часом займає метод скінченних різниць. Універсальність, можливість застосування в лінійних і нелінійних задачах роблять методскінченних різниць самим поширеним із застосованих в даний час наближених методів. Але не лише надзвичайна загальність різницевого метода приваблює дослідників, мабуть, це найбільш зручний та прозорий чисельний метод, завдяки якому майже завжди можна отримати уяву про шуканий розв’язок.

Передати ідею метода скінчених різниць можна буквально в декількох словах. Уявіть собі, що перед вами стоїть задача про знаходження наближеного розв’язку деякого диференціального рівняння.

(1)

при початкових умовах

. (2)

якщо початкові умови (2) задаються в одній точці , то сукупність звичайного рівняння і початкової умови називають задачею Коші.

Виникає питання: чи не можна спростити задане рівняння позбавившись якимось чином від похідної шуканої функції ? Найпростіший шлях розв’язання цієї задачі міститься у визначенні похідної.

, (3)

Дійсно, якщо відкинути в цій рівності знак границі, то отримаємо наближену формулу

, (4)

яка дає змогу замінити похідну різницевим відношення, розміщеним у правій частині формули (4). Похідні більш високого порядку також можуть бути апроксимовані різницевим відношенням подібного вигляду.

Таким чином, якщо всі похідні від шуканої функції , які входять у диференціальне рівняння, замінити відповідними різницевими відношеннями, що апроксимують ці похідні, то отримаємо різницеве рівняння, яке в математичному сенсі буде задачею більш простою від задачі Коші. Розв’язок отриманого різницевого рівняння, що є апроксимацією диференціального рівняння, вважають наближеним розв’язком диференціального рівняння.

В кінцево-різницевому рівнянні,яке апроксимує диференціальне, x і t є неперервні змінні, тому і саму це рівняння називається рівнянням з неперервними аргументами. Розв’язати таке рівняння важко, а часто і зовсім неможливо. У зв’язку з цим замість кінцево-різницевих рівнянь з неперервними аргументами розглядають відповідні йому різницеві рівняння з дискретними аргументами, коли незалежні змінні x і t отримують дискретну множину значень, наприклад

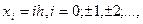(5)

де .

В результаті диференціальне рівняння замінюється кінцево-різницевим рівнянням з дискретними аргументами. Легко бачити, що таке різницеве рівняння можна тлумачити як систему лінійних алгебраїчних рівнянь стосовно невідомих , в якій число рівнянь рівне числу невідомих. Розв’язуючи отриману систему алгебраїчних рівнянь, знаходять наближені значення шуканого розв’язку . Якщо крім диференціального рівняння була задана початкова умова, то і вона також повинна бути замінена різницевими початковими умовами для функції 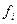, які повинні розглядатися разом з отриманою раніше системою алгебраїчних рівнянь.

Дата добавления: 2014-01-07