Лекція 5. Методи чисельного інтегрування звичайних диференціальних рівнянь

Систему звичайних диференціальних рівнянь, визначених на інтервалі часу , запишемо в загальному вигляді

(1)

Однозначність розв’язку забезпечують додаткові умови в одній або декількох точках інтервалу [a,b]. У випадку однієї точки ці умови задають найчастіше на початку інтервалу й називають їх початковими умовами

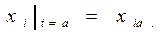(2)

Знаходження розв’язку (1),що задовольняє початковим умовами (2),називають задачею Коші. У випадку двох точок ці умови найчастіше задають на краях інтервалу й називають їх крайовими умовами

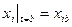(3)

Знаходження розв’язку (1), що задовольняє крайовим умовам (3),називають крайовою задачею. Вважатимемо, що розв’язок поставлених задач на [a,b] існує і є однозначний. Системи, що містять похідні вищих порядків,ми не розглядаємо, бо, вводячи нові змінні, їх завжди можна привести до вигляду (1).

Задачі для диференціальних рівнянь (Коші,крайові)розглядають у двох постановках – лінійній і нелінійній. Лінійна визначається лінійними диференціальними рівняннями і лінійними додатковими умовами. Нелінійна постановка задачі містить або нелінійні рівняння, або нелінійні умови, або те й інше.

Чисельне інтегрування диференціальних рівнянь передбачає часову дискретизацію їх похідних, у результаті чого обчислювальний процес зводиться до алгебрагічних операцій. Дискретизація здійснюється шляхом розкладання шуканих функцій в ряд Тейлора.

1.Метод Ейлера

Найпростішими з чисельних методів інтегрування диференціальних рівнянь є метод Ейлера, але ідеї, покладені в його основу, є вихідними для найширшої низки чисельних методів. Метод Ейлера ґрунтується на заміні шуканої функції многочленом першого ступеня, тобто на лінійній екстраполяції. Але при виводі цього методу, незважаючи на його простоту, ми поступимо так, щоб показати загальний підхід до побудови апроксимації диференціального рівняння на часовому кроці довільного порядку точності. А вже тоді метод Ейлера одержимо як окремий, найпростіший, випадок.

Розглянемо диференціальне рівняння

(4)

на інтервалі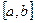. Розіб’ємо інтервал на m відрізків вузлами з постійним кроком . Точний розв’язок задачі (4) у точці на будь-якому з окремих інтервалів 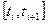, , можна представити у вигляді ряду Тейлора з центром в точці .

Вважаючи, що 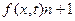раз неперервно диференційована за обома аргументами, можемо записати

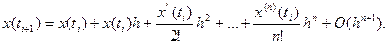(5)

Похідні в (5) обчислюються згідно з (4) таким чином:

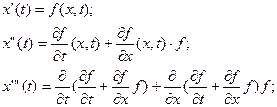(6)

Тут треба покласти – точний розв’язок (4), а затим підставити 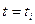. Якщо в (6) відкинути залишковий член, то одержимо таке дискретне рівняння:

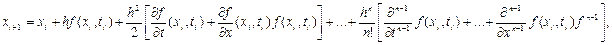(7)

де , задано в (4).

Рівняння (5) – двоточкова явна різницева схема. За нею можна послідовно обчислити всі значення , починаючи з 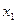і кінчаючи 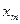. Похибка апроксимації дорівнює значенню відкинутого залишкового члена 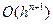при .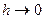

Якщо взяти 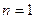, то одержуємо схему явного методу Ейлера

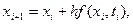(8)

точність апроксимації якої .

Якщо взяти 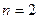, то отримаємо покращений метод Ейлера

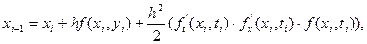(9)

точність апроксимації формули якого .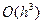

Як бачимо, для одержання різницевих схем методом рядів Тейлора треба мати аналітичні вирази повних похідних по t від функції .

2. Приклад розв’язання диференціального рівняння методом скінченних різниць.

Завдання. Використовуючи метод скінченних різниць, укласти рішення крайової задачі для диференціального рівняння з кроком h=0,1.

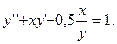
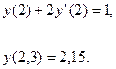
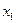
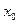
Крайові умови:

2,0 2,1 2,2 2,3

Розіб’ємо відрізок [2,0; 2,3] на частини з кроком h=0,1. Отримаємо чотири вузлові точки з абсцисами Два вузли і є кінцевими, а два інші – внутрішні.

Апроксимуємо першу і другу похідні скінченними різницями:

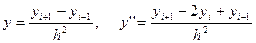(1)

і підставляємо їх у вихідне диференціальне рівняння. Отримаємо

(2)

З крайових умов складаємо різницеві рівняння в кінцевих вузлах:

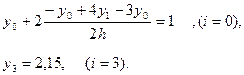(3)

Рівняння (2), (3) зводяться до розв’язання системи рівнянь:

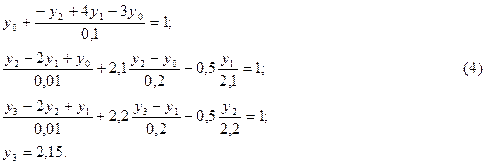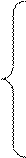Після перетворень отримаємо:

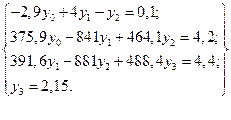(5)

Підставивши 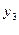у третє рівняння, отримаємо для визначення решти невідомих системи:

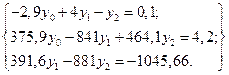(6)

Результати розв’язання (6):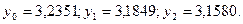

Дата добавления: 2014-01-07