
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 3. Ряды из аналитических функций. Теоремы Вейерштрасса для рядов из аналитических функций. Степенные ряды
Пусть в области 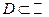 определена бесконечная последовательность однозначных функций
определена бесконечная последовательность однозначных функций 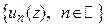 . Выражение вида
. Выражение вида 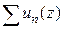 называется (формальным) функциональным рядом. Если зафиксировать некоторую точку
называется (формальным) функциональным рядом. Если зафиксировать некоторую точку 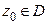 , то получаем соответствующий числовой ряд
, то получаем соответствующий числовой ряд  .
.
Определение 7. Совокупность точек 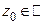 , в каждой из которых сходится числовой ряд
, в каждой из которых сходится числовой ряд  , называется областью (поточечной) сходимости функционального ряда
, называется областью (поточечной) сходимости функционального ряда 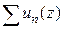 .
.
Вместе с тем, для функциональных рядов может быть введено более важное, новое понятие сходимости – равномерной.
Определение 8. Функциональный ряд 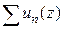 называется равномерно сходящимся в области
называется равномерно сходящимся в области 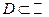 , если для
, если для 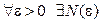 такое, что при всех
такое, что при всех 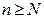 неравенство
неравенство
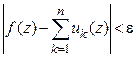
выполняется сразу для всех точек 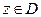 .
.
Как обычно, частичной суммой порядка 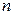 функционального ряда
функционального ряда 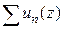 будем называть сумму
будем называть сумму 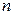 первых его членов, т.е.
первых его членов, т.е. 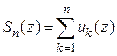 . Формально заданный ряд
. Формально заданный ряд 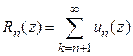 будем называть остатком порядка
будем называть остатком порядка 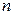 исходного функционального ряда
исходного функционального ряда 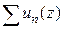 .
.
Исследовать на равномерную сходимость заданный функциональный ряд – задача достаточно трудная. Иногда в ее решении может помочь следующий критерий Коши равномерной сходимости.
Теорема 9 (критерий Коши). Для того, чтобы функциональный ряд 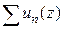 равномерно сходился в области
равномерно сходился в области  необходимо и достаточно, чтобы для
необходимо и достаточно, чтобы для 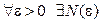 такое, что неравенство
такое, что неравенство
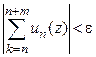 (11)
(11)
выполняется для любых номеров 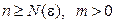 и любой точки
и любой точки 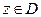 .
.
Полезным в исследованиях на равномерную сходимость является также следующий признак Вейерштрасса.
Теорема 10 (признак Вейерштрасса). Если в любой точке 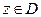 члены функционального ряда
члены функционального ряда 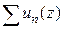 могут быть промажорированы членами сходящегося числового ряда
могут быть промажорированы членами сходящегося числового ряда  , т.е.
, т.е.
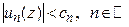 ,
,
то функциональный ряд 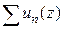 равномерно сходится в области
равномерно сходится в области  .
.
Сформулируем теперь некоторые свойства равномерно сходящихся функциональных рядов:
1º. Если все члены ряда 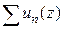 непрерывны в замкнутой области
непрерывны в замкнутой области 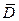 и ряд сходится равномерно, то его сумма также непрерывна в
и ряд сходится равномерно, то его сумма также непрерывна в 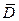 .
.
2º. Если все члены ряда 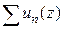 непрерывны в области
непрерывны в области  и ряд сходится равномерно, то ряд можно почленно интегрировать по любой кусочно-гладкой кривой
и ряд сходится равномерно, то ряд можно почленно интегрировать по любой кусочно-гладкой кривой 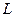 без самопересечений, целиком лежащей в
без самопересечений, целиком лежащей в  , причем ряд из интегралов сходится равномерно.
, причем ряд из интегралов сходится равномерно.
3º.Если ряд 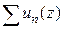 сходится равномерно в
сходится равномерно в 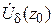 и
и 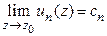 , то ряд
, то ряд  сходится и
сходится и
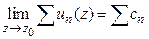 .
.
Все сформулированные выше свойства равномерно сходящихся рядов предполагали непрерывность их членов. Результат можно существенно усилить, если предполагать аналитичность функций 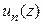 .
.
Теорема 11 (Вейерштрасса). Пусть функции 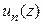 являются аналитическими в области
являются аналитическими в области  и ряд
и ряд 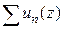 равномерно сходится в любой замкнутой подобласти
равномерно сходится в любой замкнутой подобласти 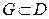 к функции
к функции  . Тогда:
. Тогда:
1)  аналитическая функций в области
аналитическая функций в области  ;
;
2) 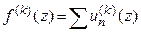 ;
;
3) ряд 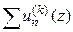 равномерно сходится в любой замкнутой подобласти
равномерно сходится в любой замкнутой подобласти 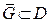 .
.
Замечание. Условие равномерной сходимости функционального ряда 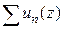 в любой замкнутой подобласти в
в любой замкнутой подобласти в  можно усилить, заменив его на равномерную сходимость в замкнутой области
можно усилить, заменив его на равномерную сходимость в замкнутой области 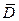 .
.
Важным частным случаем ряда аналитических функций является степенной ряд, общий член которого имеет вид 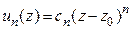 . Таким образом, функциональный ряд
. Таким образом, функциональный ряд 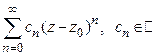 , называется общим степенным рядов (для удобства нумераций его членов начинается с нуля). К общим степенным рядам применима вся теория рядов аналитических функций, но при условии равномерной сходимости ряда. Таким образом, при исследовании общего степенного ряда важно определить область его равномерной сходимости. Для этого нам потребуется следующая теорема Абеля.
, называется общим степенным рядов (для удобства нумераций его членов начинается с нуля). К общим степенным рядам применима вся теория рядов аналитических функций, но при условии равномерной сходимости ряда. Таким образом, при исследовании общего степенного ряда важно определить область его равномерной сходимости. Для этого нам потребуется следующая теорема Абеля.
Теорема 12. Если степенной ряд 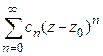 сходится в некоторой точке
сходится в некоторой точке 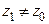 , то
, то
1) он абсолютно сходится в любой точке 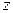 , удовлетворяющей условию
, удовлетворяющей условию 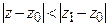 ;
;
2) в любом круге 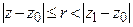 ряд сходится равномерно.
ряд сходится равномерно.
Непосредственно из результатов теоремы Абеля получаем следующие следствия:
1º. Если степенной ряд 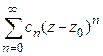 расходится в некоторой точке
расходится в некоторой точке 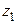 , то он расходится и во всякой точке
, то он расходится и во всякой точке 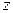 , удовлетворяющей условию
, удовлетворяющей условию 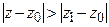 .
.
2º. Для всякого степенного ряда существует такое единственное число 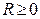 (может быть равное бесконечности), что внутри круга
(может быть равное бесконечности), что внутри круга 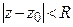 ряд сходится, а при
ряд сходится, а при 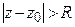 ряд расходится.
ряд расходится.
Определение 9. Область 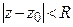 называется кругом сходимости степенного ряда, а число
называется кругом сходимости степенного ряда, а число 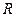 – радиусом сходимости. Радиус сходимости степенного ряда в зависимости от вида его коэффициентов может принимать любое значение в пределах от 0 до
– радиусом сходимости. Радиус сходимости степенного ряда в зависимости от вида его коэффициентов может принимать любое значение в пределах от 0 до 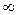 .
.
3º. В круге сходимости 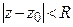 общий степенной ряд сходится к аналитической функции.
общий степенной ряд сходится к аналитической функции.
4º. Общий степенной ряд в круге сходимости можно почленно интегрировать и дифференцировать любое число раз, причем радиусы сходимости получающихся рядов равны радиусу сходимости исходного ряда.
5º. Пусть 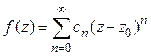 в круге сходимости. Тогда для
в круге сходимости. Тогда для 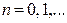 , имеют место формулы
, имеют место формулы
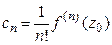 .
.
Из последнего следствия получаем, что общий степенной ряд в круге сходимости может быть записан следующим образом через свою сумму
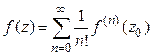 .
.
Полученный ряд называется рядом Тейлора функции  .
.
Упражнения.
33. Сформулировать на языке 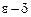 понятие поточечной сходимости ряда
понятие поточечной сходимости ряда 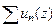 в области
в области 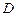 (см. определение 7).
(см. определение 7).
34. Доказать, сумма конечного числа равномерно сходящихся рядов есть равномерно сходящийся ряд.
35. Доказать: если все члены равномерно сходящегося ряда умножить на одну и ту же ограниченную функцию (в частности, константу), то равномерная сходимость не нарушается.
36. Доказать критерий Коши равномерной сходимости функционального ряда (теорема 9). Указание: записать левую часть неравенства (11) через разность соответствующих частичных сумм.
37. Доказать признак Вейерштрасса равномерной сходимости (теорема 10). Указание: рассмотреть остаточный член 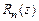 порядка
порядка 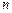 и получить его оценку через остаточный член числового ряда.
и получить его оценку через остаточный член числового ряда.
38. Показать, что ряд 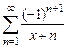 в области
в области 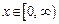 сходится равномерно, но мажорантного числового ряда для него не существует.
сходится равномерно, но мажорантного числового ряда для него не существует.
39. Показать, что ряд 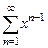 в области
в области 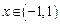 сходится неравномерно.
сходится неравномерно.
40. Доказать свойства 1º-3º равномерно сходящихся рядов.
41. Доказать п.1 теоремы Вейерштрасса. Указание. Выбрать произвольный замкнутый кусочно-гладкий без самопересечений контур 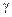 . Тогда по свойству 2º равномерно сходящихся рядов
. Тогда по свойству 2º равномерно сходящихся рядов
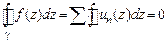 .
.
Воспользоваться теоремой Морера (см. упражнение 32).
42. Доказать п.2 теоремы Вейерштрасса. Указание. Пусть 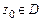 . Рассмотреть ряд
. Рассмотреть ряд
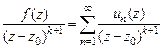
и проинтегрировать его по замкнутому, кусочно-гладкому контуру 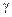 , содержащему точку
, содержащему точку 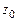 и целиком лежащему в области
и целиком лежащему в области 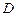 . Далее воспользоваться формулой типа Коши (10) для производных.
. Далее воспользоваться формулой типа Коши (10) для производных.
43. Доказать п.3 теоремы Вейерштрасса. Указание. Получить равномерную оценку остатка 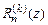 порядка
порядка 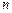 ряда из производных в любой замкнутой подобласти
ряда из производных в любой замкнутой подобласти 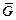 области
области 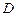 .
.
44. Доказать теорему Абеля. Указание. Заметив, что
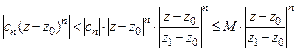 ,
,
воспользовавшись признаком сравнения рядов с положительными членами (для доказательства п.а)), либо мажорантным признаком Вейерштрасса (для доказательства п.б)).
45. Доказать следствия 1º-5º из теоремы Абеля.
46. Доказать, что для радиуса сходимости 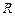 общего степенного ряда верны формулы:
общего степенного ряда верны формулы:
а) 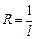 , где
, где 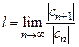 ,
,
б) 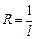 , где
, где 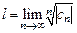 ,
,
если соответствующий предел существует. Указание. Воспользоваться признаками абсолютной сходимости Даламбера и Коши соответственно.
47. Определить радиус и круг сходимости каждого из следующих рядов:
а) 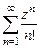 , б)
, б) 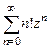 .
.
48. Доказать следующую теорему (формула Коши-Даламбера): радиус сходимости 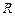 общего степенного ряда определяется формулой:
общего степенного ряда определяется формулой:
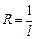 , где
, где 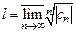 .
.
Указание. Рассмотреть отдельно случаи 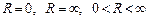 .
.
Лекция 4. Ряды Тейлора. Аналитическое продолжение. Теорема единственности для аналитической функции. Правильные и особые точки аналитической функции. Классификация особых точек.
Мы выяснили, что всякий общий степенной ряд внутри своего круга сходимости определяет некоторую аналитическую функцию. Поставим обратную задачу: можно ли аналитической функции внутри некоторого круга сопоставить степенной ряд, сходящийся в этом круге к исходной функции?
Теорема 13 (Тейлора). Функция  , аналитическая внутри круга
, аналитическая внутри круга 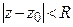 , может быть представлена в этом круге сходящимся степенным рядом
, может быть представлена в этом круге сходящимся степенным рядом
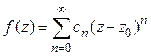 , (12)
, (12)
коэффициенты которого однозначно определяются по формулам
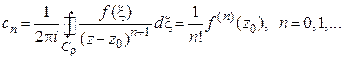 , (13)
, (13)
где 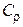 – окружность радиуса
– окружность радиуса 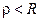 с центром в точке
с центром в точке 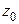 .
.
Формулы (12) и (13) представляют собой разложение в ряд Тейлора аналитической функции. В частном случае, когда 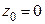 соответствующее разложение называется рядом Маклорена. Ниже представлены разложения в ряд Маклорена основных аналитических функций:
соответствующее разложение называется рядом Маклорена. Ниже представлены разложения в ряд Маклорена основных аналитических функций:
1º. 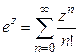 .
.
2º. 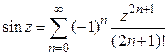 .
.
3º. 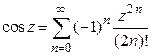 .
.
4º. 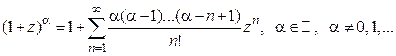 .
.
Теорема Тейлора позволяет заключить, что для аналитической функции ее задание в каждой точке области аналитичности совершенно не обязательно. Действительно, в некотором круге аналитическая функция однозначно определяется коэффициентами ряда Тейлора, которые в соответствии с формулами (13) определяются значениями на внутренней окружности. В более общей ситуации теорема Коши позволяет однозначно восстановить аналитическую в области  функцию по ее значениям на границе. Поэтому возникает вопрос о той минимальной информации, которая необходима для однозначного восстановления аналитической
функцию по ее значениям на границе. Поэтому возникает вопрос о той минимальной информации, которая необходима для однозначного восстановления аналитической  .
.
Лемма. Пусть  аналитическая в области
аналитическая в области  функция, обращающаяся в нуль в различных точках
функция, обращающаяся в нуль в различных точках 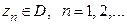 . Если последовательность
. Если последовательность 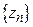 сходится к
сходится к 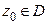 , то
, то 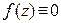 в
в  .
.
Теорема 14 (единственности). Пусть в области  заданы две аналитические функции
заданы две аналитические функции  и
и 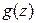 . Если в области
. Если в области  существует последовательность различных точек
существует последовательность различных точек 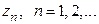 , сходящаяся к некоторой точке
, сходящаяся к некоторой точке 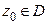 , и
, и 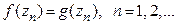 , то
, то 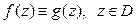 .
.
В некоторых вопросах может быть полезна другая формулировка теоремы единственности.
Теорема 14 a. Если 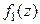 и
и 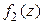 аналитические, соответственно, в областях
аналитические, соответственно, в областях 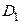 и
и 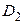 функции совпадают в области
функции совпадают в области 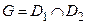 , то существует единственная аналитическая функция такая, что
, то существует единственная аналитическая функция такая, что
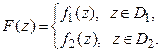 (14)
(14)
Последняя теорема позволяет ввести понятие аналитического продолжения аналитической функции.
Определение 10 (Принцип аналитического продолжения). Пусть на комплексной плоскости 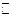 заданы две области
заданы две области 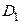 и
и 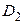 , имеющие общую часть (которая может быть как односвязна, так и многосвязна), Пусть аналитические функции
, имеющие общую часть (которая может быть как односвязна, так и многосвязна), Пусть аналитические функции 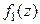 и
и 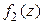 , заданные, соответственно, в областях
, заданные, соответственно, в областях 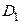 и
и 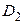 , либо
, либо
- совпадают на пересечении 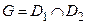 ;
;
- совпадают на компоненте 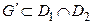 , а на второй компоненте
, а на второй компоненте 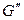 – различны.
– различны.
В обоих случаях функция 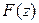 вида (14) является аналитической в области
вида (14) является аналитической в области 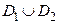 и называется аналитическим продолжением
и называется аналитическим продолжением 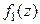 на область
на область 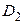 (соответственно, аналитическим продолжением
(соответственно, аналитическим продолжением 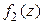 на область
на область 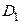 ).
).
Отметим, что во втором случае определения 10 мы получаем многозначную аналитическую функцию 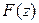 , т.к. для любой точки
, т.к. для любой точки 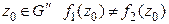 .
.
Пусть в области  задана однозначная аналитическая функция
задана однозначная аналитическая функция 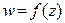 .
.
Определение 11. Точка 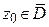 (замыканию области
(замыканию области  ) называется правильной точкой аналитической функции
) называется правильной точкой аналитической функции  , если существует степенной ряд
, если существует степенной ряд 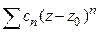 с положительным радиусом сходимости:
с положительным радиусом сходимости: 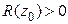 такой, что в общей части области
такой, что в общей части области  и круга сходимости он сходится к
и круга сходимости он сходится к  .
.
В противном случае, точка 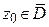 называется особой для аналитической функции
называется особой для аналитической функции  . Можно сформулировать положительное определение особой точки.
. Можно сформулировать положительное определение особой точки.
Определение 12. Точка 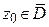 называется особой точкой аналитической функции
называется особой точкой аналитической функции  , если для любого степенного ряда
, если для любого степенного ряда 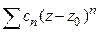 с положительным радиусом сходимости в общей части круга сходимости ряда и области
с положительным радиусом сходимости в общей части круга сходимости ряда и области  найдется, по крайней мере, одна точка
найдется, по крайней мере, одна точка 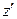 , в которой сумма степенного ряда не равна
, в которой сумма степенного ряда не равна  .
.
Нетрудно видеть, что все внутренние точки области  являются правильными для
являются правильными для  , так что особые точки
, так что особые точки  могут располагаться только на границе
могут располагаться только на границе 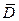 .
.
Классификация особых точек:
Точка 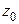 называется изолированной особой точкой аналитической функции
называется изолированной особой точкой аналитической функции  , если существует такая
, если существует такая 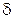 -окрестность точки
-окрестность точки 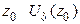 , в которой нет других особых точек.
, в которой нет других особых точек.
В противном случае точка 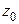 называется неизолированной особенностью
называется неизолированной особенностью  . Таким образом, точка
. Таким образом, точка 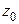 – неизолированная особая точка аналитической функции
– неизолированная особая точка аналитической функции  , если в любой окрестности точки
, если в любой окрестности точки 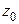 существует, по крайней мере, еще одна особая точка
существует, по крайней мере, еще одна особая точка  .
.
Различают три типа изолированных особых точек аналитической функции:
1º. Точка 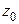 называется устранимой особой точкой, если существует конечный
называется устранимой особой точкой, если существует конечный 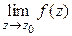 .
.
2º. Точка 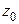 называется полюсом, если
называется полюсом, если 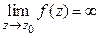 .
.
3º. Точка 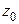 называется существенно особой, если
называется существенно особой, если 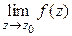 не существует.
не существует.
Упражнения.
49. Доказать теорему Тейлора. Указание. Представить 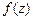 по формуле Коши:
по формуле Коши:
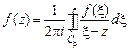
и преобразовать подынтегральное выражение, используя формулу суммы бесконечно убывающей геометрической прогрессии:
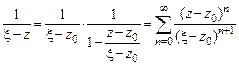 .
.
50. Доказать формулы разложений в ряд Маклорена 1º-4º и найти радиусы сходимости соответствующих рядов.
51. Получить разложения в ряд Маклорена следующих функций:
а) 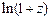 ; б)
; б) 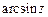 ;
;
в) 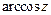 ; г)
; г) 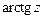 ;
;
д) 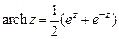 ; е)
; е) 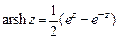 .
.
52. Доказать лемму о равенстве нулю аналитической функции. Указание. Разложить 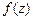 в ряд Тейлора в некоторой окрестности точки
в ряд Тейлора в некоторой окрестности точки 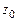 . Имеем
. Имеем 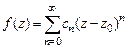 и в силу непрерывности
и в силу непрерывности 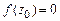 . Поэтому
. Поэтому 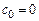 , так что
, так что 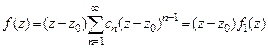 . Заметить, что
. Заметить, что 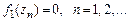 , и повторить рассуждения.
, и повторить рассуждения.
53. Доказать теорему единственности для аналитической функции. Указание. Применить лемму о равенстве нулю к функции 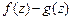 .
.
54. Доказать теорему 14А.
55. Показать, что функция 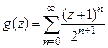 является аналитическим продолжением функции
является аналитическим продолжением функции 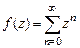 с области
с области 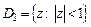 на область
на область 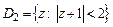 .
.
56. Показать, что функция для 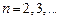
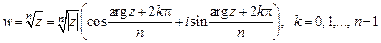
является n -значной аналитической функцией на всей комплексной плоскости, кроме точки 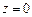 .
.
57. Для следующих функций определить особые точки и выяснить их характер:
а) 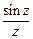 ; б)
; б) 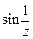 ; в)
; в) 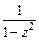 .
.
|
Дата добавления: 2014-01-07; Просмотров: 3919; Нарушение авторских прав?; Мы поможем в написании вашей работы!