Специальные символы

# – префикс непосредственного операнда

@ – префикс косвенной адресации

(х) – содержимое регистра или прямо адресуемого байта

((R_i)) – содержимое ячейки РПД, адресуемой содержимым

регистра R_i (i = 0, 1);

¬ – оператор присваивания (замещения)

«– оператор взаимного обмена

Ù, Ú, Å – операторы логических операций: И (конъюнкция),

ИЛИ (дизъюнкция), исключающее ИЛИ

Н – суффикс шестнадцатеричного кода

Лекция 1

СТРУКТУРА АВТОМАТИЗИРОВАННОГО ЭКСПЕРИМЕНТА

В настоящее время невозможно представить себе физический эксперимент, который не был бы полностью или частично автоматизирован. Каждый такой эксперимент можно представить обобщенной структурной схемой (рис. 1.1). В экспериментальной установке воспроизводится исследуемое явление. Она может содержать десятки тысяч элементов и блоков, необходимых для задания и поддержания определенных условий проведения эксперимента. Для этой цели экспериментальная установка снабжается системой управления. Результаты эксперимента в виде изменяемых или постоянных (что крайне редко) физических величин должны быть преобразованы с помощью первичных преобразователей (иногда их называют датчиками или сенсорами) в электрический сигнал. Например, изменение температуры может быть преобразовано в изменение сопротивления медной или платиновой проволоки, в изменение разности потенциалов на термопаре, в изменение падения напряжения на р – n- пере-ходе и т. д. Собственно первичные преобразователи могут представлять достаточно сложные физические системы, в которых происходит одно или несколько преобразований искомой физической величины в другую физическую величину, а затем в электрический сигнал, например, γ-кванты преобразуются в световые фотоны с помощью соответствующих кристаллов, затем фотоны, взаимодействуя с металлическим катодом фотоэлектронного умножителя (ФЭУ), выбивают из него электроны. Затем происходит их умножение в ФЭУ в тысячи раз, что воспринимается нагрузкой как непрерывный импульсный ток. Для задания требуемого коэффициента усиления изменяют напряжение на динодах ФЭУ с помощью управления источником питания ФЭУ. В связи с тем, что по напряжению (току) на выходе первичного преобразователя рассчитывают значения физической величины, наиболее просто это осуществить, когда между выходным напряжением и физической величиной существует линейная связь.

Первичные преобразователи для многих физических экспериментов проектируются индивидуально для каждой экспериментальной установки. Однако существуют и унифицированные преобразователи, например температуры или другой физической величины в электрический сигнал. Сигнал на выходе первичного преобразователя может изменяться от очень малых величин, соизмеримых с его собственными шумами, до достаточно больших величин, ограниченных сверху допустимыми нелинейными искажениями. Для некоторых экспериментов динамический диапазон изменения сигналов может составлять 100–120 дБ.

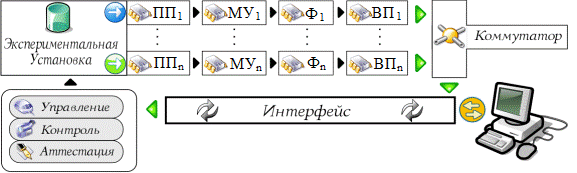
Рис. 1. 1. Структурная схема автоматизированного эксперимента. Здесь: ПП₁ – ПП _n – первичные преобразователи (датчики) физических величин в электрические сигналы; МУ₁ – МУ _n – масштабирующие устройства (усилители, делители) электрических сигналов; Ф₁ – Ф _n – фильтры; ВП₁ – ВП _n – вторичные преобразователи аналоговых электрических сигналов в цифровые сигналы

Как известно, эксперименты можно разделить на качественные
и количественные. Как правило, качественные эксперименты редко автоматизируются. Для количественного эксперимента необходимо установить количественную связь, описывающую состояние экспериментальной установки, поэтому для этой цели аналоговые электрические сигналы на выходе первичных преобразователей должны быть преобразованы в цифровые данные с помощью специальных вторичных преобразователей, которые носят название аналого-цифровых преобразователей. В настоящее время аналого-цифровые преобразователи унифицированы и выпускаются серийно, поэтому они работают с сигналами заданного размера. В то же время первичные преобразователи, как правило, не унифицированы, поэтому для согласования выходных сигналов первичных преобразователей и допустимых входных уровней вторичных преобразователей существуют масштабирующие устройства (усилители
и делители).

Согласно теореме отсчетов для преобразования непрерывных аналоговых сигналов в цифровую форму необходимо осуществить не менее N преобразований в секунду, причем:

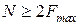
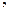(1.1)

где F_max – максимальная частота в спектре преобразуемого сигнала.

Так как спектр ограниченного во времени сигнала не ограничен по F_max, то для исключения эффекта наложения спектров после преобразования сигналов вторичными преобразователями необходимо по входам вторичных преобразователей (ВП) включить соответствующие фильтры низших частот.

Эффект наложения спектров продемонстрирован на рис. 1.2.

Для уменьшения эффекта наложения спектров можно увеличить частоту преобразования (частоту дискретизации F _дискр) или ограничить спектр сигнала, подаваемого на вторичный преобразователь. Ограничение спектра исходного сигнала естественно приводит к его искажению в области высоких частот (искажение мелких деталей процесса), поэтому такое ограничение должно выполняться исходя из условия допустимых искажений (допустимой погрешности) исследуемого процесса. Ограничение спектра выполняют с помощью включения фильтра низких частот (ФНЧ) n -го порядка. Порядок фильтра определяют в зависимости от допустимой погрешности преобразования исследуемого процесса, которая определяется неравенством :

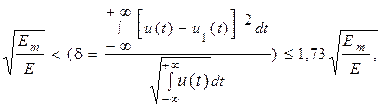(1.2)

где Е – полная энергия спектра, u (t) – исходный сигнал, u ₁ (t) – сигнал, восстановленный рядом Котельникова, Е_m – энергия, сосредоточенная в высокочастотной части спектра выше частоты дискретизации, δ – относительная погрешность восстановления сигнала.

Между первичным преобразователем и вторичным преобразователем иногда включают фильтр верхних частот, что исключает передачу постоянной составляющей в исследуемом сигнале. Такое включение вызвано наличием смещения масштабирующих усилителей, которое, суммируясь с постоянной составляющей сигнала, может исказить сигнал при его усилении за счет ограниченного динамического диапазона как самого усилителя, так и вторичного преобразователя (рис. 1.3).

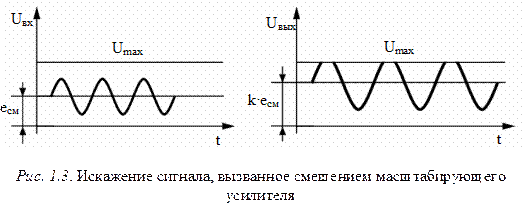
С другой стороны, включение фильтра верхних частот может вызвать искажение амплитуды при усилении однополярных импульсов, если изменяется их частота и скважность, поэтому, выбирая параметры фильтра, необходимо учитывать эти искажения. Так как фильтр верхних частот должен препятствовать влиянию напряжения смещения усилителя на искажение искомого сигнала, то место его включения должно быть перемещено в то место масштабирующего усилителя, где сигнал уже превышает напряжение смещения, но напряжение смещения еще не приводит к искажению формы сигнала.

На выходе вторичных преобразователей вырабатываются цифровые данные с частотой дискретизации, причем для каждого вторичного преобразователя (ВП) может быть выбрана своя частота дискретизации. Однако могут быть случаи, когда частота дискретизации для нескольких ВП совпадает. Данные с выхода ВП должны поступать в электронную вычислительную машину (ЭВМ) в темпе их частот дискретизации, но если ЭВМ по своим скоростным данным не успевает принимать поток данных с какого-либо канала, то в этом канале данные предварительно могут накапливаться в специальном запоминающем устройстве, построенном по принципу FIFO (первым пришел, первым ушел). Следует, однако, помнить, что такая организация возможна при преобразовании однократных сигналов и только в том случае, когда ЭВМ успевает принимать, обрабатывать и выдавать (сохранять) весь поток данных от экспериментальной установки. Если ЭВМ не справляется с такой задачей, то в некоторых каналах может быть включена индивидуальная ЭВМ, а ЭВМ на рис. 1.1
в этом случае используется для окончательной обработки данных и выдачи результатов эксперимента. Для последнего случая ЭВМ в канале может быть заменена микропроцессором. В этом случае такой канал можно рассматривать как интеллектуальный первичный преобразователь.

Если частота дискретизации относительно малая, то данные с ВП могут поступать в ЭВМ через коммутатор.

Для обеспечения передачи данных от ВП (коммутатора) в ЭВМ служит специальное устройство – интерфейс. Это устройство в зависимости от ЭВМ, ВП и потока данных от каждого канала работает в одном из соответствующих режимов, часть интерфейса может находиться на плате ЭВМ, а часть – в электронном блоке, обслуживающем экспериментальную установку. Интерфейс и его режимы будут рассмотрены в последних лекциях курса, посвященных ЭВМ. Когда аналоговые сигналы в каналах изменяются с малыми скоростями и имеется быстродействующий ВП, то один ВП может быть подключен к нескольким каналам через аналоговый коммутатор. Такое включение может несколько удешевить электронный блок за счет уменьшения количества ВП. Однако следует к такому решению относиться с осторожностью, так как в этом случае возникает опасность воздействия более сильных сигналов одних каналов на слабые сигналы других каналов. Такое искажение слабых сигналов может произойти в аналоговом коммутаторе за счет ошибок в его проектировании.

Для управления экспериментальной установкой служит обратный канал, передающий информацию от ЭВМ к установке. По этому каналу передается информация как для преобразования цифровых данных в аналоговые сигналы, например для изменения уровня питания ФЭУ, уровня питания отдельных узлов установки, так и для изменения коэффициентов усиления усилителей, изменения конфигурации экспериментальной установки, выполнения режима пуска, остановки и т. д.

Другая задача обратного канала может заключаться в выполнении функций контроля работоспособности установки путем подачи в те или иные точки экспериментальной установки так называемых тестовых сигналов. Если тестовые сигналы, вырабатываемые специальными устройствами, имеют стандартную форму с предварительно измеренными параметрами, то они могут быть использованы не только для контроля работоспособности установки, но и для оценки метрологических характеристик основных ее частей. Следует отметить, что тестовые сигналы должны поддерживать свои характеристики с более высокой точностью (в 3–4 раза превышающей допустимую точность каналов экспериментальной установки.

Некоторые физические эксперименты могут занимать большие пространства, соизмеримые даже с площадью Земли, а некоторые эксперименты выносят за пределы Земли. В этом случае эксперимент дополняется системой точного времени для датирования сигналов и, как правило, измерительный канал или совокупность измерительных каналов одного района объединяются локальной ЭВМ. В центральную ЭВМ эксперимента данные с локальных ЭВМ передаются по радиоканалу, причем эти данные сопровождаются меткой точного времени. В зависимости от полосы частот сигналов в измерительных каналах точность задания времени (количество значащих цифр) может изменяться.

Следует отметить, что в первичных преобразователях часто применяют аналоговую обработку сигналов, которая характеризуется высокой скоростью и относительной простотой. Однако ее недостаток – низкая помехозащищенность, сложность изменения в процессе работы алгоритма обработки. Вследствие этого аналоговую обработку стремятся заменить цифровой обработкой. Для цифровой обработки выпускают цифровые интегральные схемы (ИС) малой и средней степени интеграции (вентили, регистры, шифраторы, дешифраторы, мультиплексоры и т. д.), а также большие ИС, которые содержат огромное количество элементов малой и средней степени интеграции. Эти большие ИС могут изготавливаться для решения определенных задач автоматизации или могут перепрограммироваться пользователем для создания элементов автоматизированных установок. В составе большой ИС могут находиться микропроцессоры, микроконтроллеры, усилители, вторичные преобразователи, цифровые фильтры, интерфейсы и т. д. Для того чтобы ориентироваться в огромном море различных элементов и систем автоматизации и предназначены лекции настоящего учебного пособия по автоматизации физического эксперимента.

Лекция 2

ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ
В ЦИФРОВЫХ УСТРОЙСТВАХ

В состав систем автоматизации входит цифровой процессор, представляющий собой устройство, которое осуществляет обработку информации, представленной в цифровой форме. Изучение цифровых устройств целесообразно начать с ознакомления с позиционными системами счисления и способами перевода чисел из одной системы счисления в другую.

2.I. Системы счисления и коды

Кодом называют систему условных знаков (символов), используемых для передачи, обработки и хранения информации. Конечная последовательность этих знаков образует кодовую комбинацию или слово. Число различных символов, используемых в словах данного кода, называется его основанием.

Для записи кода используют цифры, буквы или специальные знаки, например «.» (точка) и «–» (тире) и т. д. В технике для обозначения кодового символа используют элементарные сигналы, которые обладают какими-либо физическими параметрами, способными принимать несколько значений. Для электрических сигналов такими параметрами могут быть амплитуда напряжения или тока, полярность или длительность импульсов и т. д.

Системой счисления называют совокупность приемов и правил наименования и обозначения чисел, позволяющую установить взаимно однозначное соответствие между любым числом и его представлением в виде кодовой комбинации. Различают позиционные и непозиционные системы счисления.

Непозиционные системы счисления. В непозиционных системах счисления число выражается кодовой комбинацией, в которой значение каждого символа определяется только его конфигурацией. Примерами таких систем являются унитарная и римская системы счисления. В унитарной системе счисления используется всего один элементарный символ (например, единица), а значение кодовой комбинации определяется количеством этих символов. В римской системе счисления используются символы для обозначения десятичных разрядов (I = 1, Х= 10, С = 100, M = 1000) и их половин (V = 5, L = 50, D = 500). Числа записываются в виде определенных комбинаций этих символов. При этом значения нескольких стоящих рядом одинаковых символов суммируются (III = 1 + + 1 + 1 = 3). Если младший символ стоит справа от старшего символа, то их значения также суммируются (VI = 5 + 1 = 6). Если младший символ стоит слева от старшего, то значение младшего символа вычитается из значения старшего символа (IV = 5 – 1 = 4).

Непозиционные системы счисления в цифровых устройствах не получили широкого распространения из-за сложных и громоздких алгоритмов представления чисел и выполнения арифметических операций.

Позиционные системы счисления. В позиционных системах счисления значение символа определяется не только его конфигурацией, но и позицией в кодовой комбинации. В этих системах счисления используется конечный набор символов, количество которых называется основанием системы счисления. Значимость каждой позиции (разряда) кодовой комбинации определяется весовым коэффициентом, или весом.

В позиционных системах счисления с непосредственным представлением чисел для каждой цифры имеется отдельный символ. Позиционная система счисления, в которой каждая цифра кодируется определенной комбинацией нескольких символов, называется системой с кодированным представлением чисел.

В позиционной системе счисления с непосредственным представлением чисел число A может быть записано в виде

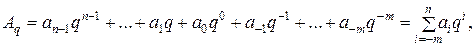(2.1)

где А_q – произвольное число, записанное в системе счисления с основанием q, a_i –цифры (символы) системы счисления, i – номер разряда, n и m – количество разрядов в целой части и дробной части числа соответственно.

Как видно из выражения (2.1), вес каждого разряда кодовой комбинации в позиционной системе счисления определяется ее основанием в степени, равной номеру разряда. Это обстоятельство позволяет записать выражение (2.1) в более простой форме

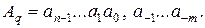(2.2)

В выражении (2.2) целая часть числа отделяется от дробной части числа запятой, разряд с наибольшим весом, обычно называемый старшим значащим разрядом (СЗР), записывается крайним слева, а крайним справа записывается младший значащий разряд (МЗР), имеющий наименьший во всей кодовой комбинации вес.

Количество разрядов в записи числа, обычно называемое длиной числа или длиной разрядной сетки, определяет максимальное А_(q)max и минимальное А_(q)min по абсолютному значению числа. Если длина разрядной сетки равна целому положительному числу, например n, то А_(q)max= qⁿ – 1 и А_(q)min = – (qⁿ – 1). Интервал числовой оси, заключенный между максимальным А_(q)max и минимальным А_(q)min числами, называется диапазоном представления чисел в заданной системе счисления.

Основными преимуществами позиционных систем счисления по сравнению с непозиционными системами счисления являются удобство представления чисел и простота выполнения арифметических операций. Недостаток позиционных систем – невозможность выполнения арифметических операций как поразрядных. Поразрядной операцией называют такую, результат которой в любом разряде не зависит от результата выполнения этой операции во всех остальных разрядах.

Позиционные системы счисления представлены в цифровой технике кодами, обычно называемыми позиционными или весовыми.

Одной из представительниц позиционных систем счисления является десятичная система. Для изображения в ней любого числа используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Основание десятичной системы счисления 10, а таблица весов имеет вид:

10 ^{n –1}...10¹ 10⁰ 10^–1...10^{– m}.

Двоичная система счисления. Почти во всех цифровых устройствах для представления чисел применяется двоичная система счисления – система, основание которой равно 2. В ней используются только два символа: 0 и 1.

Каждый разряд двоичной записи числа называется битом (сокращение английских слов binary digit, означающих – «двоичный знак»). Веса младших десяти битов двоичного числа имеют следующие значения:

2^9	2^8	2^7	2^6	2^5	2^4	2^3	2^2	2^1	2^0

Четырехразрядное двоичное слово называют тетрадой, а восьмиразрядное – байтом.

Представление чисел в восьмеричной и шестнадцатеричной системах счисления. Одним из недостатков двоичной системы счисления является большая, чем в других позиционных системах счисления, длина кодовой комбинации. Например, десятичное число 47₁₀ в двоичной системе счисления имеет вид 101111₂. Здесь и далее индексы введены для обозначения системы счисления.

Для сокращения записи двоичных чисел используются восьмеричная и шестнадцатеричная системы счисления. Основание восьмеричной системы счисления – 8, шестнадцатеричной – 16. Используемые в этих системах символы и их десятичные и двоичные эквиваленты приведены в табл. 2.1.

Для того чтобы записать целое двоичное число в восьмеричном (шестнадцатеричном) коде, необходимо разбить его на группы по три (четыре) бита, начиная с МЗР, а затем каждую группу заменить ее восьмеричным (шестнадцатеричным) эквивалентом в соответствии с табл. 2.1.

Таблица 2.1 Восьмеричные и шестнадцатеричные числа и их десятичные и двоичные эквиваленты
Десятичное число	Двоичное число	Восьмеричное число	Шестнадцатеричное число
			A
			B
			C
			D
			E
			F

Пример. Перевести в восьмеричную и шестнадцатеричную системы счисления число A = 11101100101₂.

Р е ш е н и е.

11101100101₂ = 11 101 100 101₂ = 3545₈.

11101100101₂ = 111 0110 0101₂ = 765₁₆.

Для обратного преобразования достаточно заменить каждую восьмеричную или шестнадцатеричную цифру числа двоичным эквивалентом.

Двоично-десятичные коды. В цифровых устройствах позиционные системы счисления с кодированным представлением чисел представлены двоично-десятичными кодами. Применение этих кодов позволяет использовать при запоминании и отображении десятичных цифр известные достоинства двоичных кодов (простота технической реализации и др.). В то же время эти коды сохраняют преимущества десятичной системы счисления, состоящие в удобстве и легкости восприятия результатов обработки данных в цифровых устройствах человеком.

Переход к двоично-десятичному представлению десятичных чисел осуществляется заменой каждого разряда десятичного числа группой из четырех двоичных символов (двоичных тетрад), которые не обязательно имеют такие же весовые коэффициенты, как в двоичной системе счисления.

Наибольшую известность получил двоично-десятичный код 8-4-2-1, в котором десятичные цифры кодируются соответствующими четырехразрядными двоичными числами (табл. 2.2). Само название «код 8-4-2-1» отражает значение весовых коэффициентов битов кода. В дальнейшем этот код будем называть просто двоично-десятичным кодом, а иные двоично-десятичные коды будем оговаривать особо.

Рассмотренный двоично-десятичный код относится к так называемым взвешенным кодам, каждый разряд которых имеет постоянный весовой коэффициент. Двоично-десятичный код с избытком 3, приведенный в табл. 2.2, относится к невзвешенным кодам. Разряды этого кода не имеют весовых коэффициентов. Переход к представлению десятичного числа в коде с избытком 3 осуществляется прибавлением 3₁₀ к каждому десятичному разряду исходного числа, представленного в двоично-десятичном коде 8-4-2-1. Достоинства кода с избытком 3 связаны с тем, что изображения в этом коде двух десятичных чисел, равных в сумме 9, следуют одно из другого при взаимной замене нулей на единицы, а единиц – на нули. Коды, обладающие таким свойством, называются самодополняющимися.

Код Грея. Рассматриваемый ниже код является наиболее распространенным представителем циклических кодов. Они характеризуются тем, что каждая последующая комбинация двоичных цифр отличается от предыдущей комбинации только в одном разряде (табл. 2.3). Это свойство оказывается полезным при некоторых способах преобразования измеряемого параметра в код. Преимуществом кода Грея перед другими циклическими кодами является простота преобразования двоичного или двоично-десятичного кода в код Грея и обратно.

Параллельный и последовательный коды. Существуют два класса цифровых устройств, различающиеся формой представления двоичных чисел: устройства последовательного и устройства параллельного действия. В устройствах параллельного действия каждый из разрядов двоичного параллельного кода представлен электрическим сигналом, действующим в отдельном проводе, причем кодовые сигналы действуют во всех разрядных линиях одновременно. В устройствах последовательного действия электрические сигналы, представляющие разряды последовательного двоичного кода, формируются последовательно во времени, один за другим, и информация, отображаемая этой последовательностью электрических сигналов, может быть передана из одной точки пространства в другую по одной линии связи (в простейшем случае необходим один информационный провод и один земляной провод).

2.2. Кодирование символов

Цифровое устройство непосредственно может оперировать только с числами. Для представления в цифровых устройствах как числовой, так и нечисловой информации используются так называемые алфавитно-цифровые коды. В этих кодах допускается кодирование десятичных цифр, букв алфавита, специальных символов, таких как знаки препинания или знаки арифметических операций, а также символов управляющих операций, таких как «возврат каретки».

Наибольшее распространение получил код ASCII (American Standard Code for Information Interchange – Американский стандартный код для обмена информацией). Набор его символов приведен в табл. 2.4.

2.3. Перевод чисел из одной системы счисления

в другую

Применение двоичной системы счисления в цифровых устройствах делает необходимым перевод исходных данных из десятичной системы счисления в двоичную систему, а результатов расчета – из двоичной системы счисления в десятичную. При этом могут встретиться три случая: перевод целых чисел; перевод правильных дробей; перевод неправильных дробей.

Таблица 2.4 Таблица символов кода ASCII
Двоичный код	Старшие разряды
Младшие разряды		NUL	DLE	SP		@	P	×	p
	SON	DC 1	!		A	Q	a	q
	STX	DC 2	“		B	R	b	r
	ETX	DC 3	#		C	S	c	s
	EOT	DC 4	$		D	T	d	t
	ENQ	NAK	%		E	U	e	u
	ACK	SYN	&		F	V	f	v
	BEL	ETB	‘		G	W	g	W
	BS	CAN	(		H	X	h	X
	HT	EM	)		I	Y	i	Y
	LF	SUB	*	:	J	Z	j	Z
	VT	ESC	+	;	K	[	k	{
	FF	FS	,	<	L	\	l	|
	CR	GS	-	=	M	m	M	}
	SO	RS	.	>	N	­	n	~
	SI	US	/	?	O	_	o	DEL

О б о з н а ч е н и я: NUL – пусто; SON – начало заголовка; STX – начало текста; ETX – конец текста; EOT – конец передачи; ENQ – запрос; ACK – подтверждение; BEL – звонок; BS – возврат на шаг; HT – горизонтальная табуляция; LF – перевод строки; VT – вертикальная табуляция; FF – перевод формата; CR – возврат каретки; SO – национальный регистр; SI – латинский регистр; DLE – авторегистр; DC 1 – управление устройством 1; DC 2 – управление устройством 2; DC 3 – управление устройством 3; DC 4 – управление устройством 4; SYN – синхронизация; NAK – отрицание; ETB – конец блока; CAN – аннулировано; EM – конец носителя; SUB – подстановка; ESC – авторегистр 2; FS – разделитель файла; GS – разделитель группы; RS – разделитель записи; US – разделитель элемента записи; SP – пробел; DEL – стирание.

Перевод целых чисел. Для перевода целых чисел из системы счисления с основанием q 1 в систему счисления с основанием q 2 преобразуемое число делят на основание q 2 по правилам деления системы счисления с основанием q 1. Деление продолжают до тех пор, пока не получат частное, целая часть которого равна нулю. При этом остаток, полученный при первом делении на q 2, представляет собой МЗР числа в системе счисления q 2 с весовым коэффициентом 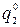, остаток от второго деления представляет собой разряд искомого числа с весовым коэффициентом 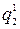и т. д. Последний остаток является СЗР искомого числа.

Пример. Перевести из десятичной системы счисления в двоичную систему счисления число А = 26₁₀.

Р е ш е н и е:

26: 2 = 13, остаток 0.

13: 2 = 6, остаток 1.

6: 2 = 3, остаток 0.

3: 2 = 1, остаток 1.

1: 2 = 0, остаток 1.

Ответ: А = 26 ₁₀ = 11010 ₂.

Рассмотренный метод перевода целых чисел из одной системы счисления в другую называется методом деления. Применение его не вызывает затруднений, если исходной системой счисления является десятичная система счисления. При необходимости перевода чисел из недесятичной системы счисления в десятичную систему счисления применение этого метода становится нецелесообразным ввиду затруднений, возникающих при выполнении арифметических операций в недесятичной системе счисления. В этом случае лучше воспользоваться выражением (2.1), в соответствии с которым необходимые арифметические действия выполняются в десятичной системе счисления.

Пример. Перевести числа А₁ = 1111110₂ и А₂ = 7Е₁₆ в десятичную систему счисления.

Р е ш е н и е:

1111110₂ = 1∙2⁶ + 1∙2⁵ +1∙2⁴ + 1∙2³ + 1∙2² + 1∙2¹ =126₁₀,

7E₁₆ = 7∙16¹ + 14∙16⁰ = 126₁₀.

Ответ: А₁ = 126₁₀, А₂ = 126₁₀.

Перевод правильных дробей. Перевод правильных дробей из системы счисления с основанием q 1 в систему счисления с основанием q 2 осуществляется путем умножения по правилам умножения исходной системы счисления самой исходной дроби, а затем дробной части получаемых произведений на основание q 2. Умножение производится до тех пор, пока не достигается требуемая точность представления дроби. Правильная дробь в системе счисления q 2 формируется из целых частей, получаемых в процессе перевода произведений. При этом старшим разрядом результата является целая часть первого произведения.

Пример. Перевести из десятичной системы счисления в двоичную правильную дробь А = 0,4375₁₀.

Р е ш е н и е: 0,4375∙2 = 0,8750

0,875∙2 = 1,750

0,75∙2 = 1,5

0,5∙2 = 1,0.

Ответ: А = 0,0111₂.

Рассмотренный метод перевода правильных дробей называется методом умножения. Как и метод деления, этот метод удобен при переводе из десятичной системы счисления в недесятичную систему счисления. Если же исходной системой является какая-либо недесятичная система, как и в случае целых чисел, целесообразно воспользоваться выражением (2.1).

Пример. Перевести из двоичной системы счисления в десятичную правильную дробь А = 0,0111₂.

А = 1∙2^–2 + 1∙2^–3 + 1∙2^–4 = 0,4375₁₀.

Перевод неправильных дробей. При переводе неправильных дробей из недесятичной системы счисления в десятичную систему счисления целесообразно воспользоваться выражением (2.I). Если же исходной является десятичная система счисления, при переводе неправильной дроби используют методы деления и умножения, отдельно преобразуя целую и дробную части исходной дроби.

Лекция 3

ОСНОВЫ БУЛЕВОЙ АЛГЕБРЫ

Описание поведения цифровых устройств осуществляется с помощью раздела математической логики – алгебры логики, возникшей в середине ХIХ века в трудах английского ученого Дж. Буля, по имени которого она часто называется булевой алгеброй.

Основное понятие алгебры логики – высказывание. Под вы-сказыванием понимают любое предложение, оцениваемое только с точки зрения его истинности или ложности. Для обозначения истинности высказывания используется цифра 1, для обозначения ложности – 0. Эти символы в дальнейшем будем называть логическим нулем и логической единицей или просто нулем и единицей.

В соответствии со способностью высказываний принимать только одно из двух возможных значений условились называть их булевыми (логическими) переменными и обозначать буквами латинского алфавита.

Высказывания могут быть простыми и сложными. К простым высказываниям относятся такие высказывания, значения которых не зависят от иных высказываний. При анализе и синтезе цифровых устройств простые высказывания рассматриваются как независимые переменные.

Высказывание называется сложным, если его значение зависит от значений каких-либо иных высказываний. Сложные высказывания называют булевыми (логическими) функциями простых высказываний, входящих в их состав и являющихся их аргументами.

В булевой алгебре, как и в математическом анализе, справедлив принцип суперпозиции функций, в соответствии с которым вместо аргумента данной функции может быть подставлена другая функция. В соответствии с этим принципом сложная булева функция может быть представлена суперпозицией более простых булевых функций.

Ограниченный набор булевых функций, обеспечивающий на основе принципа суперпозиции построение булевых функций любой сложности, называется функционально полным набором булевых функций (базисом).

3.1. Булевы функции одной и двух переменных

Значение булевой функции определяется значением ее аргументов (переменных). Любая совокупность этих значений, расположенная в каком-либо определенном порядке, называется набором значений переменных или просто набором. Набор булевой функции n переменных представляет собой n -разрядное двоичное слово, десятичный эквивалент которого принято считать его номером. Для любой булевой функции n переменных существует 2 ⁿ различных наборов.

Так как булева функция n переменных определена на 2 ⁿ наборах и может принимать только 2 значения, то число различных булевых функций n переменных равно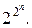

Наиболее употребительны два способа задания булевой функции: табличный и аналитический. В первом случае функцию задают в виде таблицы, в левой части которой записаны в порядке возрастания номеров двоичные наборы переменных, а в правой – значение функции для каждого набора. Такие таблицы называются таблицами истинности.

Число строк таблицы истинности булевой функции равно числу различных наборов ее аргументов. Если функция зависит от n аргументов, то число различных наборов аргументов функции равно 2 ⁿ, поскольку каждый набор имеет свой номер, а общее число номеров равно количеству различных n -разрядных чисел.

Аналитический способ описания состоит в задании булевых функций с помощью аналитических выражений, часто называемых структурными формулами.

Булевы функции одной переменной. Простейшими булевыми функциями являются функции одной переменной (табл. 3.1). Их всего 4. Функции f ₀(x) = 0 и f ₃(x) = 1 представляют собой константы 0 и 1, а функция f ₁(x) = = х просто повторяет значения аргумента х. Единственной нетривиальной функцией является функция f ₂(x), получившая название инверсии (отрицания) переменной х и обозначаемая .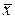

Булевы функции двух переменных. Булевы функции двух переменных представлены в табл. 3.2. Из приведенных в ней 16 функций функции f ₀ = 0 и f ₁₅ = 1 являются константами, f ₁₀ = х ₀ и f ₁₂ = х ₁ – повторением переменных, а f ₃ = 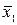и f ₅ = 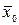– инверсиями переменных. Остальные 10 функций являются нетривиальными. Они имеют свое название и обозначение.

Функция f ₈ называется конъюнкцией, логическим умножением или логическим И. Для ее обозначения используется символ «Ù» (f ₈ = x ₁Ù x ₀), знак арифметического умножения (f ₈ = x ₁· x ₀) символ «&» (f ₈ = x ₁ &x ₀) или вообще не используют никаких символов (f ₈ = x ₁ x ₀).

Функция f ₁₄ получила название дизъюнкции, логического сложения или логического ИЛИ. Для ее обозначения наряду с символом Ú (f ₁₄ = = x ₁Ú x ₀) используется знак арифметического сложения (f ₁₄ = x ₁ + x ₀).

Система функций И, ИЛИ и НЕ образует так называемый основной базис булевых функций. Существуют и другие функционально полные системы булевых функций. К ним относятся прежде всего функции f ₁ и f ₇.

Функция f ₁ называется стрелкой Пирса, функцией Пирса или отрицанием дизъюнкции (ИЛИ-НЕ). Для ее обозначения используется стрелка, разделяющая переменные (f ₁ = х ₁¯ х ₀), используют также запись f ₁ = 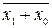. Последнее обозначение, как и название «отрицание дизъюнкции», указывает на то, что рассматриваемая функция может быть получена суперпозицией функций дизъюнкции и отрицания. Функционально полную систему, образованную функцией Пирса, обычно называют базисом Пирса.

Функция f ₇ называется штрихом Шеффера, функцией Шеффера или отрицанием конъюнкции (И-НЕ). Для ее обозначения наряду с вертикальной чертой, разделяющей переменные (f ₇ = х ₁| х ₀),используют также запись f ₇ = 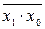.Функция Шеффера может быть получена суперпозицией функций конъюнкции и отрицания. Она образует функционально полную систему, называемую базисом Шеффера.

Функция f ₆ принимает единичное значение при несовпадении значений ее аргументов. Она получила название «исключающее ИЛИ» («неравнозначность»). Часто она называется также суммой по модулю 2. Для обозначения этой функции обычно используют запись f ₆ = х ₁ Å х ₀.

Функция f ₉ называется функцией равнозначности или эквивалентности. Обозначается знаком равнозначности f ₉ = x ₁ º x ₀.

Функции f ₂, f ₄, f ₁₁ и f ₁₃ (табл. 3.2) менее употребительны.

Представление булевых функций с помощью электрических схем.
В одной из самых ранних технических интерпретаций логических высказываний, предложенной петербургским физиком П. Б. Эрнефестом в начале ХХ века, использовалась аналогия между высказываниями и переключателями, имеющими, как и высказывания, двоичную природу. Любое истинное высказывание в соответствии с такой интерпретацией изображается замкнутым контактом переключателя, а любое ложное – разомкнутым контактом. Принятая аналогия позволяет реализовать булевы функции с помощью соединенных соответствующим образом переключателей. Например, последовательное включение переключателей реализует функцию И (рис. 3.1, а), а параллельное – ИЛИ (рис. 3.1, б).

Только в том случае, если оба контакта (и А, и В) переключателей замкнуты (рис. 3.1, а), положительное напряжение подается на анод светоизлучающего диода VD 1. Он оказывается включенным в прямом направлении, через него протекает ток и он излучает.

Светоизлучающий диод VD 2 будет излучать, если какой-либо из контактов (или А, или В) или оба сразу окажутся замкнутыми (рис. 3.1, б). Если же оба ключа будут разомкнуты, диод VD 2 излучать не будет.

В современных цифровых устройствах логические высказывания отображаются электрическим напряжением, имеющим два различных уровня: высокий и низкий. Этим уровням в так называемой положительной логике ставят в соответствие логическую единицу и логический нуль, а в отрицательной логике высокий уровень напряжения соответствует логическому нулю, низкий – логической единице. Принятая аналогия позволяет реализовать булевы функции с помощью транзисторов, работающих в ключевом режиме.

Простейшая схема на биполярном транзисторе, реализующая булеву функцию «отрицание» входной величины А, приведена на рис. 3.2. При нулевом входном напряжении, соответствующем напряжению логического нуля, транзистор закрыт (находится в состоянии отсечки) и напряжение на его коллекторе равно напряжению источника питания (положительное напряжение, принятое за напряжение логической единицы). Если же на вход подано положительное напряжение, соответствующее логической единице, транзистор находится в состоянии насыщения и напряжение на его коллекторе близко нулю, т. е. равно напряжению логического нуля. Таким образом, рассмотренная схема реализует булеву функцию 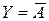, т. е. является инвертором.

Быстродействие рассмотренной схемы в значительной степени ограничено задержкой переключения транзистора из состояния насыщения в состояние отсечки. Эта задержка обусловлена наличием в области базы избыточного количества неосновных носителей, накопленных в режиме насыщения. Паразитные емкости С 1 и С 2, образованные емкостями транзистора, входной емкостью последующей схемы, емкостью монтажа, также ограничивают быстродействие инвертора, вызывая увеличение длительности фронта и среза выходного сигнала.

y

x₀

x₁

Цифровые схемы, реализующие простейшие булевы функции над входными сигналами согласно правилам булевой алгебры и формирующие выходные сигналы, соответствующие значениям реализуемых функций, называются логическими элементами. На рис. 3.3 приведены условные графические обозначения наиболее распространенных логических элементов.

НЕ

3.2. Основные законы булевой алгебры

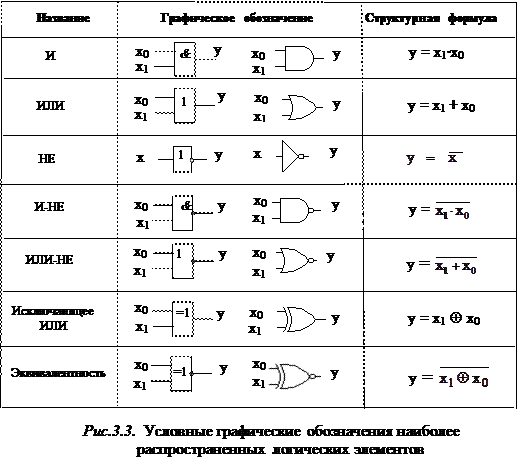
Табличный способ задания булевых функций достаточно громоздок и неудобен для анализа их свойств. Альтернативой ему является задание булевых функций с помощью структурных формул, представляющих собой суперпозицию функций отрицания, дизъюнкции и конъюнкции. Они определяют те логические операции или действия, которые необходимо произвести над переменными функции для того, чтобы получить ее значение.

Структурные формулы служат основой для построения цифровых устройств, реализующих заданные булевы функции. Правила их преобразования определены основными законами булевой алгебры и их следствиями.

Наиболее важные из теорем, отражающие основные законы булевой алгебры, приведены в табл. 3.3.

Таблица 3.3

Дата добавления: 2014-01-07