Гномостереографическая проекция

Гномостереографическую проекцию применяют чаще всего для изображения кристаллических многогранников. При этом проектируют не многогранник, а его полярный комплекс.

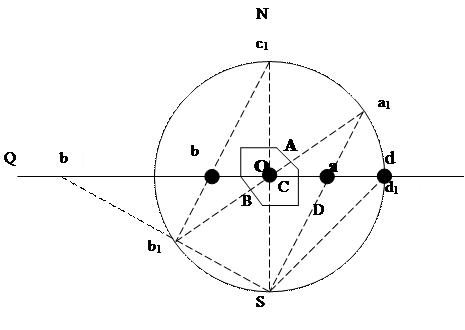
Плоскостью гномостереографической проекции служит та же экваториальная плоскость сферы проекций, как и для стереографической проекции. Для построения гномостереографической проекции кристалла на все его грани перпендикуляры и продолжить их до пересечения с поверхностью сферы проекций, описанной вокруг центра тяжести кристалла и далее провести линию, соединяющую полюсные точки с точкой зрения (рис. 5.22).

Нормали к граням, пересекающие шар проекции в верхней полусфере, проектируются внутри круга проекций (нормаль ОА, ОС) (рис.5.22, а). Нормали, пересекающие шар проекций в нижней полусфере, проектируются вне этого круга (нормаль ОВ (рис.5.22, б)).

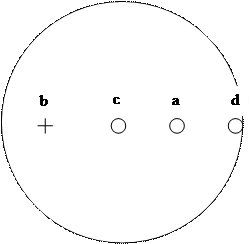
Неудобство построения заставляет переносить для таких нормалей точку зрения в северный полюс сферы. В этом случае и проекции низших граней окажутся внутри круга проекций. Чтобы отличить друг от друга проекции нормалей к верхним и нижним граням, первые обозначают кружками, вторые – крестиками (рис.5.22, б).

Гномостереографические проекции направлений (ребер кристалла) изображают также, как нормали к граням.

Комплекс граней, нормали к которым лежат в одной плоскости, образует зону проекций граней, принадлежащих одной зоне, располагаются на одной дуге большого круга.

а б

Рис.5.22 Построение гномостереографической проекции граней В, С, Д кристалла: а- принцип построения проекции; б изображение проекций граней

Контрольные вопросы

1. Дайте понятие прямого кристаллического комплекса.

2. Объясните, что такое обратный (полярный) кристаллический комплекс.

3. Запишите, какими сферическими координатами характеризуют положение точки на поверхности сферы и как их определяют.

4. Опишите положительные и отрицательные моменты при применении сферической проекции.

5. Объясните, какие комплексы изображения кристалла применяют в сферической проекции.

6. Покажите на рисунке, что является плоскостью стереографической проекции, точкой зрения.

7. Опишите и зарисуйте (на любом примере) принцип построения стереографической проекции направления.

8. Опишите и зарисуйте (на любом примере) принцип построения стереографической проекции плоскости.

9. Объясните, какой кристаллический комплекс используют для построения стереографической проекции.

10. Объясните, что является стереографической проекцией направления.

11. Объясните, что является стереографической проекцией плоскости.

12. Объясните, какой кристаллический комплекс используют в гномостереографической проекции.

13. Покажите на примере принцип построения гномостереографической проекции плоскости.

14. Покажите на примере принцип построения гномостереографической проекции направления.

15. Объясните, что является плоскостью гномостереографической проекции.

Дата добавления: 2014-01-07