Линейное уравнение множественной регрессии

(1.10)

Наименование переменных и параметров. Учет влияния случайных факторов. В общем виде линейной уравнение множественной регрессии можно записать следующим образом:

y = a₁x₁ + a₂x₂ + … +a_nx_n + b + ε,

где y – результативный признак (зависимая, результирующая, эндогенная переменная);

n – число факторов, включенных в модель;

x₁, x₂, …, x_n – признаки-факторы (регрессоры, объясняющие, предикторные, предопределенные, экзогенные переменные);

a₁, a₂, …, a_n – коэффициенты регрессии;

b – свободный член регрессии;

ε - компонента, отражающая в модели влияние случайных факторов, из-за которых реальное значение показателя может отклоняться от теоретического (регрессионный остаток).

По своей природе результирующая переменная всегда случайна. Регрессионный остаток позволяет отразить в модели стохастическую, вероятностную природу экономических процессов. Кроме того, можно также сказать, что он отражает все прочие не учтенные в явном виде факторы, которые могут повлиять на результат.

В дальнейшем в этом разделе, рассматривая способы построения уравнения регрессии, случайную компоненту пока не будем учитывать, т.е. будем рассматривать только детерминированную часть результата.

Экономический смысл параметров регрессии. Коэффициенты и свободный член регрессии принято также называть параметрами регрессии, или параметрами модели.

Коэффициенты регрессии a₁, a_2, …, a_n, как видно из записи модели, представляют собой частные производные результата по отдельным признакам-факторам:

(1.11)

Они показывают, на сколько изменяется результативный признак при изменении соответствующего признака на единицу и неизменных значениях остальных признаков (например, в формуле (1.9) коэффициент a показывает, на сколько изменится спрос на продукт при изменении цены на единицу). Поэтому иногда коэффициент линейной регрессии называют также предельной эффективностью фактора.

Знак коэффициента линейной регрессии всегда совпадает со знаком коэффициента корреляции, так как положительная корреляция означает, что результат растет с ростом фактора, а отрицательная – что с ростом фактора результат убывает.

Однако, сравнение коэффициентов регрессии при различных признаках-факторах между собой представляется затруднительным, поскольку различные факторы обычно имеют разные единицы измерения, характеризуются различными значениями средних и показателями вариации. Чтобы решить эту проблему, рассчитывают стандартизованные коэффициенты регрессии (см. далее). В отличие от стандартизованных коэффициентов регрессии коэффициенты регрессии a₁, a_2, …, a_n принято называть коэффициентами чистой регрессии.

Свободный член регрессии b показывает значение признака-результата при условии, что все признаки-факторы равны нулю. Если такая ситуация невозможна, свободный член может и не иметь экономического содержания.

Частные уравнения регрессии. На основе линейного уравнения множественной регрессии могут быть получены частные уравнения регрессии, в которых все факторы, кроме обычно одного, закреплены на своем среднем уровне. Такое частное уравнение регрессии устанавливает связь между результативным признаком и одним из признаков-факторов при условии, что остальные факторы приравнены к своим средним значениям. Система таких уравнений выглядит следующим образом:

(1.12)

где 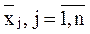- средние значения признаков-факторов.

Подстановкой в формулу (1.12) конкретных значений средних можно получить следующую систему линейных уравнений:

(1.13)

,

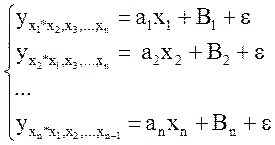где

(1.14)

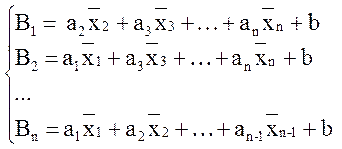
Кроме того, можно построить частные уравнения регрессии и для нескольких независимых переменных, т.е. закрепить на среднем уровне все факторы, кроме нескольких.

На основе частных уравнений регрессии могут быть построены так называемые частные коэффициенты эластичности Э_i, которые рассчитываются по формулам и показывают, на сколько процентов изменится результат при изменении фактора x_i на 1%. Расчет этих коэффициентов позволяет оценить, какие факторы более сильно воздействуют на результативный признак. Таким образом, их тоже можно использовать при отборе факторов в регрессионную модель.

Стандартизованное уравнение регрессии [Лукин]. Перейдем от переменных модели y, x₁, x₂, …, x_n к так называемым стандартизованным переменным по следующим формулам:

(1.15)

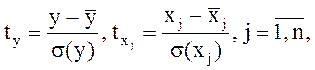
где 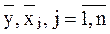- средние значения признаков;

- средние квадратические отклонения признаков.

Для новых переменных среднее значение равно нулю, а среднее квадратическое отклонение равно единице.

Стандартизованное уравнение регрессии (или уравнение регрессии в стандартизованном масштабе) строится следующим образом:

(1.16)

,

где - стандартизованные переменные;

α₁, α₂, …, α_n – стандартизованные коэффициенты регрессии.

Для нахождения стандартизованных коэффициентов используют матрицу парных коэффициентов корреляции (1.6). Можно доказать, что для стандартизованных коэффициентов регрессии выполняется следующая система уравнений[4]:

(1.17)

Она представляет собой систему n уравнений для n переменных, и ее можно использовать для определения стандартизованных коэффициентов регрессии. Эти коэффициенты можно сравнивать друг с другом и соответственно сравнивать различные факторы по силе воздействия на результат.

Можно доказать, что для линейной модели формулу (1.7) для расчета коэффициента множественной корреляции можно преобразовать в формулу, основанную на использовании стандартизованных коэффициентов регрессии:

(1.18)

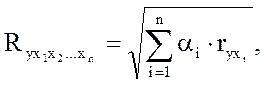
где α_i – стандартизованные коэффициенты регрессии,

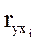- парные коэффициенты корреляции результата с каждым из факторов.

Подставив в стандартизованное уравнение регрессии (1.16) вместо стандартизованных переменных формулы (1.15), можно вернуться к уравнению чистой регрессии[5].

[1] Парную линейную регрессию еще иногда называют простой регрессией.

[2] Формулы для нелинейных функций приведены для случая, когда имеется один признак-фактор, хотя эти функции можно использовать и в случае множественной регрессии.

[3] Можно показать, что показательная и экспоненциальная функция – одно и то же. Действительно, пусть у = ab^x = a(e^{ln b})^x = ae^{x*ln b} = aе^bx, где
b = ln b.

[4] Формула (1.17) получена из формулы (1.6) следующим образом: правые части уравнений получены путем перемножения стандартизованных коэффициентов на столбцы матрицы (1.6), начиная со второго столбца и второй строки. В левой части – первая строка матрицы (1.6). Аналогичный результат можно получить, если перемножать коэффициенты на строки, а в левой части оставить первый столбец.

[5]

Дата добавления: 2014-01-07