Виды матриц

1⁰. Квадратная матрица

Определение 1.3. Матрицы называется квадратной, если число строк матрицы равно числу ее столбцов. Число ее строк (столбцов) называется порядком квадратной матрицы.

В частности, квадратные матрицы 1-го, 2-го и 3-го порядков имеют, соответственно, вид:

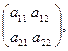
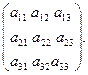(1.3)

Элементы 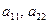матрицы 2-го порядка и элементы матрицы 3-го порядка образуют, так называемые, главные диагонали этих матриц; элементы 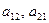и элементы 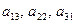образуют побочные диагонали этих матриц.

Пример. Матрица является квадратной матрицей 3-го порядка.

Главную диагональ матрицы 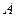образуют элементы: 5; 12; 8, а побочную – элементы: 13;12;11.

2⁰. Диагональная матрица

Определение 1.4. Квадратная матрица называется диагональной, если все ее элементы, не лежащие на главной диагонали, равны нулю.

Пример. Матрицаявляется диагональной матрицей 3-го порядка.

3⁰. Единичная матрица

Определение 1.5. Диагональная матрица называется единичной, если все элементы ее главной диагонали равны 1 :Единичная матрица обозначается символом

Единичные матрицы 1-го, 2-го и 3-го порядков имеют, соответственно, вид:

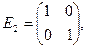
4⁰. Треугольная матрица

Определение 1.6. Квадратная матрица называется треугольной, если все ее элементы, лежащие выше или ниже главной диагонали равны нулю.

Пример. Матрицы и

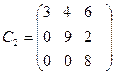является треугольными матрицами 3-го порядка.

5⁰. Нуль-матрица

Определение 1.7 Матрица любых размеров называется нуль – матрицей (нулевой матрицей), если все ее элементы равны нулю. Нулевая матрица обозначается символом

Пример. Матрица 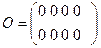является нуль – матрицей размеров .

6⁰. Матрица – строка

Определение 1.8. Матрица размеров называется матрицей – строкой: .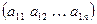

7⁰. Матрица – столбец

Определение 1.9. Матрица размеров называется матрицей – столбцом: .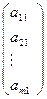

Замечание. Матрицу – строку и матрицу – столбец часто называют векторами (соответственно n-мерным и m-мерным).

2. Определители квадратных матриц
второго и третьего порядков

Определение 2.1. Определителем второго порядка, соответствующим квадратной матрице 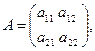называется число, обозначаемое одним из символов , , 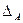просто или 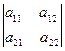и вычисляемое по формуле:

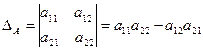. (2.1)

Пример.

Определение 2.2. Определителем третьего порядка, соответствующим квадратной матрице, 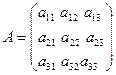называется число, обозначаемое одним из символов 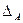, просто , или 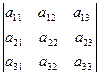и вычисляемое по формуле:

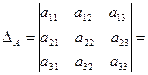
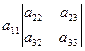
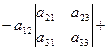
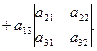(2.2)

Пример.

.

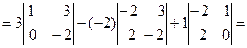
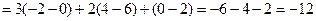Определение 2.3. Минором элемента 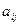, , 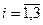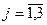определителя третьего порядка называется определитель второго порядка, получаемый из исходного определителя вычеркиванием i-ой строки и j-го столбца (то есть строки и столбца, содержащих данный элемент).

Минор элемента 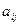обозначается символом.

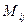Например, в матрице

:

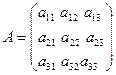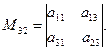
Задача 2.1. Дан определитель

Найти .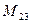

Решение. Вычеркивая вторую строку и третий столбец данного определителя, получим:

.

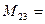
Определение 2.4. Алгебраическим дополнением 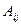элемента 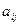определителя третьего порядка называется произведение его минора на множитель :

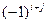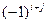
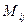
Например,

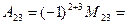
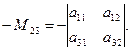
С учетом данного определения равенство (2.2) примет вид:

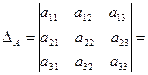
(2.3)

Справедливо следующее утверждение.

Теорема 2. 1. Определитель третьего порядка равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения.

Эта теорема позволяет вычислять значение определителя, раскрывая (разлогая) его по элементам любой строки или столбца. Например,

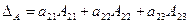(разложение по 2 строке),

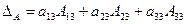(разложение по 3 столбцу).

Задача 2.2. Вычислить определитель: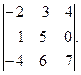

Решение. Разложим определитель по третьему столбцу. Это целесообразно, так как и поэтому алгебраическое дополнение нуля можно не считать.

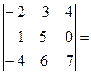
Дата добавления: 2014-01-07