Распределение Пуассона. Говорят, что случайная величина Х имеет распределение Пуассона, если её возможные значения: 0,1,2,

Говорят, что случайная величина Х имеет распределение Пуассона, если её возможные значения: 0,1,2, …, m, … (бесконечное, но счетное множество значений), а соответствующие вероятности выра­жаются формулой

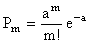(m=0,1,2,…). (5.2.1)

Распределение Пуассона играет большую роль в практическом применении теории вероятностей: многие физические явления приводят именно к такому распределению вероятностей.

Закон Пуассона (5.2.1) зависит от одного параметра а, смысл которого в следующем: он является од­новременно математическим ожиданием и дисперсией случайной величины Х, распределенной по за­кону Пуассона. Докажем это.

Воспользуемся для этого производящей функцией j(z) случайной величины Х:

j(z)=.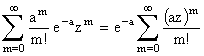

Сумма в последнем выражении есть не что иное, как e^az, поэтому

j(z)=e^-a×e^az=e^a(z-1). (5.2.2)

Чтобы найти математическое ожидание величины Х, продифференцируем производящую функцию (5.2.2) по z:

j’(z)=ae^a(z-1)

и положим в ней z=1; получим m_x= a.

Дифференцируя второй раз, найдем

j”(z)=a²e^a(z-1); j”(1)= a ² (5.2.3)

Найдем второй начальный момент:

a₂=j”(1)+m_x=a²+a.

Дисперсию случайной величины Х выразим через a₂ и m_x:

D_x=a₂-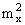=a²+a-a²=a.

Итак, параметр а пуассоновского распределения равен одновременно математическому ожиданию и дисперсии случайной величины Х, имеющей это распределение. Найдем среднее квадратическое отклоне­ние:

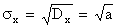. (5.2.4)

Коэффициент вариации для случайной величины Х, распределенной по закону Пуассона, равен

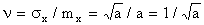(5.2.5)

и стремится к нулю при увеличении а.

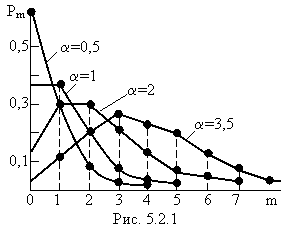
Многоугольники распределения для случайной величины Х, распределенной по закону Пуассона с параметрами а=0,5; а=1,0; а=2; а=3,5 показаны на рис. 5.2.1.

Упражнение 1. Группа надежности некоторого предприятия получила отчеты об отказах клапанов за 10 рабочих дней. Количество отказов было равно соответственно 3, 3, 2, 5, 4, 3, 2, 1, 3, 4. Чему равна оценка интенсивности отказов в расчете на один день?

Ответ: =3.

Упражнение 2. Найти оценку вероятности Р₀ того, что за один день не произойдет ни одного отказа.

Ответ: 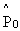@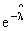=e^-3=0,05.

Упражнение 3. Пусть получена дополнительная информация, что в течение одного дня было в среднем N=500 переключений клапанов. Найти оценку вероятности безотказной работы клапана при одном переключении.

Ответ: .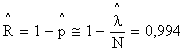

Пример 1. Предположим, что в результате предыдущих испытаний была получена оценка 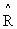=0,97. Тогда можно сделать заключение, что 80% отказов не было доложено. Дальнейшее исследование группы надежности может обнаружить, что доложены только «безусловные» отказы, в то время, как в предыдущих отчетах давались сведения как о безусловных, так и о «частичных» отказах.►

Рассмотрим условия, при которых возникает пуассоновское распределение.

Прежде всего покажем, что оно является предельным для биномиального, когда число опытов n не­ограниченно увеличивается (n®¥) и одновременно параметр р (вероятность «успеха» в одном опыте) неограниченно уменьшается (р®0), но так, что их произведение np сохраняется в пределе постоянным и равным а:

.

Из предыдущего пункта мы знаем, что математическое ожидание случайной величины Х, распреде­ленной по биномиальному закону с параметрами n и р, равно np. Мы обозначили np=a. Для случайной величины Х, имеющей биномиальное распределение с параметрами n и a/n,

P{X=m}=.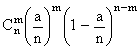

Посмотрим, каков будет предел этого выражения при n®¥:

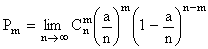. (5.2.6)

Преобразуем выражение, стоящее под знаком предела в формуле (5.2.6):

.

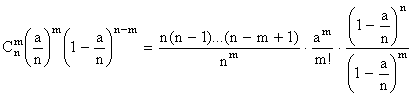Первая дробь и знаменатель последней дроби при постоянном m и n ®¥ стремятся к единице. Пре­образуем числитель последней дроби к виду

.

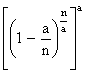В пределе при n®¥ это выражение, как мы знаем из курса математики, стремится к е^-а. Следова­тельно, предельное значение в формуле (5.2.6) равно

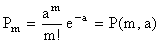, (5.2.7)

а это и есть распределение Пуассона.

Из доказанного предельного свойства следует, что распределение Пуассона с параметром a=np можно приближенно применять вместо биномиального, когда число опытов n очень велико, а вероят­ность р очень мала, т.е. в каждом отдельном опыте событие А появляется крайне редко. Отсюда проис­ходит применяющееся ещё иногда для закона Пуассона название «закон редких явлений».

В свое время «классическим» примером случайной величины Х, распределенной по закону Пуассона, приводившемся во многих учебниках, было «число солдат-кавалеристов, убитых за год ударом копыта лошади». Число опытов n здесь – число встреч солдат-кавалеристов с лошадью, а р – вероятность того, что встреча закончится столь плачевно. Статистические данные показали хорошее совпадение распре­деления случайной величины Х с пуассоновским. В настоящее время этот пример, по понятным причи­нам, потерял свою актуальность. Однако и в наше время есть задачи, где распределением Пуассона можно пользоваться вместо биномиального. Например, если речь идет о многократном применении технического устройства высокой надежности, такой, что вероятность отказа при одном применении очень мала.

Для контроля возможности замены биномиального распределения пуассоновским можно на всякий случай подсчитать одну-две ординаты точного, биномиального, распределения и сравнить с теми, кото­рые получаются по приближенному, пуассоновскому.

Помимо этого предельного случая возникновения пуассоновского распределения, на практике встре­чается ряд ситуаций, где это распределение имеет место.

Рассмотрим, например, такую задачу. Пусть на оси времени 0 t случайным образом возникают точки – моменты появления каких-то однородных событий (например, отказов устройств, поступлений информации в АСУ, приходов посетителей в магазин, вызовов на телефонной станции и т.п.). Последовательность таких моментов обычно называют «потоком событий». Предположим, что поток обладает следующими свойствами.

1. Стационарность. Это свойство означает, что вероятность попадания того или иного числа событий на участок времени длины t не зависит от того, где на оси 0 t расположен этот участок, а зависит только от его длины t. Из этого следует, что среднее число событий, появляющихся в единицу времени, постоянно. Обозначим его l и будем называть интенсивностью потока.

2. Ординарность. Это свойство означает, что события возникают поодиночке, а не группами по два, по три и т.д. Точнее, ординарность потока выражается в том, что вероятность попадания на малый участок D t двух или более событий пренебрежимо мала по сравнению с вероятностью попадания на него одного события (при D t ®0 вероятность попадания на участок D t более чем одного события – бесконечно малая более высокого порядка малости, чем вероятность попадания на него же ровно одного события).

3. Отсутствие последействия. Это свойство означает, что вероятность попадания того или другого числа событий на заданный участок оси 0 t не зависит от того, сколько событий попало на любой другой не пересекающийся с ним участок (в частности, «будущее» потока не зависит от его прошлого; отсюда и термин «отсутствие последействия»). Эта независимость физически сводится к тому, что события появляются на оси времени в силу случайных причин, индивидуальных для каждого из них.

Поток событий, обладающий этими тремя свойствами – стационарностью, ординарностью и отсутствием последействия, называется простейшим (или стационарным пуассоновским) потоком.

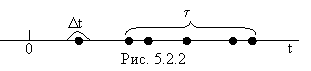
Простейший поток тесно связан с распределением Пуассона. Действительно, возьмём на оси 0 t участок времени длиной t (рис.5.2.2) и докажем, что случайная величина X – число событий, попадающих на этот участок, имеет распределение Пуассона. Разделим мысленно участок t на n равных частей длины D t =t/ n. Математическое ожидание числа событий, попадающих на элементарный участок D t, очевидно, равно lD t, где l - интенсивность потока. Согласно свойству 2 (ординарности) потока можно

пренебречь вероятностью попадания на элементарный участок D t двух и более событий.

Назовём элементарный участок D t «занятым», если на нём появилось событие из потока, и «свободным» – если не появилось, и введём индикатор U события «участок D t занят»:

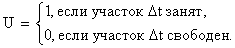
Математическое ожидание индикатора события «участок D t занят» равно вероятности этого события:

M[U]= p _Dt,

где p _Dt – вероятность того, что участок D t будет занят.

Среднее число – математическое ожидание – числа событий, попадающих на участок D t, очевидно, равно

M[U]=lDt,

откуда находим

p _Dt=lDt=.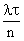

Теперь рассмотрим n участков оси 0 t, как n независимых опытов (независимость следует из свойства 3 потока), в каждом из которых может появиться событие А={участок занят} с вероятностью lD t. Число занятых элементарных участков – это число Х событий на всем участке t (если ни на каком из элементарных участков не может появиться более одного события; в пределе при D t ®0 это будет именно так). Случайная величина Х имеет биномиальное распределение

с параметрами n и .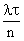

Теперь будем неограниченно увеличивать число элементарных участков D t и найдем в пределе (при n ®¥) вероятность того, что на участок t попадет ровно m событий:

.

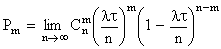Но мы только что доказали, что при условии n ®¥, 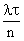®0 и постоянном значении произведения n×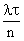=lt биномиальное распределение стремится к пуассоновскому с параметром lt:

.

Таблицы значений функции 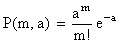приводятся в соответствующей литературе.

Таким образом, мы выяснили ещё один тип условий, в которых возникает распределение Пуассона.

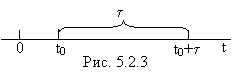
Отметим (сделаем это без специального доказательства), что условие 1 (стационарность потока) не является обязательным для того, чтобы число событий, попадающих на участок длины t, распределялось по закону Пуассона (достаточно, чтобы выполнялись условия 2 и 3). Если интенсивность потока событий l не постоянна, а зависит от времени l=l(t), то вероятность попадания ровно m событий на участок длины t, начинающийся в точке t ₀ и кончающийся в точке t ₀+t (рис. 5.2.3), имеет тоже распределение Пуассона: 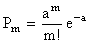(m=0,1,2,…), где .

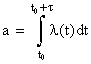Добавим к этому, что ось 0 t, на которой случайным образом появляются точки, вовсе не обязательно должна быть осью времени, а точки на ней – моментами появления событий. Картина может иметь другой физический смысл (например, точки причаливания к берегу лодок, действующих независимо друг от друга).

Более того, закон Пуассона может возникать в результате появления случайных точек не только на оси, а на плоскости или в пространстве. В таких случаях говорят не о «потоке событий», а о поле точек на плоскости (см. рис.5.2.4) или в пространстве.

Три условия, обеспечивающие простейший характер потока для поля точек, формулируются в виде:

1. Однородность поля – это значит, что вероятность попадания того или иного числа точек в какую-то фигуру S (см. рис.5.2.4) (объём) не зависит от того, где эта фигура (объём) находится, а зависит только от её площади (объёма).

2. Ординарность поля – это значит, что точки на плоскости (в пространстве) появляются поодиночке, а не по две, по три и т.д. Точнее, что вероятность попадания в элементарный участок плоскости (пространства) двух или более точек пренебрежимо мала по сравнению с вероятностью попадания одной точки.

3. Отсутствие взаимодействия в поле – это означает, что вероятность попадания того или иного числа точек в плоскую (или пространственную) фигуру не зависит от того, сколько точек попало в любую другую непересекающуюся с ней фигуру.

Роль интенсивности l потока событий в случае поля точек играет его плотность l - среднее число точек, попадающих в единицу площади (объема). Для однородного поля точек l=const; для неоднородного l зависит от координат точки (х,у) на плоскости; (х,у,z) – в пространстве.

Можно доказать (мы этого делать не будем), что для поля, обладающего всеми тремя свойствами, число точек, попадающих в заданную плоскую (пространственную) фигуру, распределено по закону Пуассона с параметром а, равным ls, где s – площадь фигуры (или lv, где v – объем фигуры).

Для того, чтобы возникало распределение Пуассона, не обязательно соблюдение всех трех условий, достаточно соблюдения двух последних (ординарности и отсутствия взаимодействия). Если такое поле неоднородно, то число точек, попадающих в плоскую (пространственную) фигуру, вычисляется по формулам

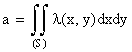(для плоскости)

или 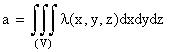(для пространства).

Двойной интеграл распространяется на всю плоскую фигуру S, а тройной – на всю пространственную фигуру V.

Для вычисления различных вероятностей, связанных с законом Пуассона, полезно пользоваться функцией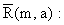

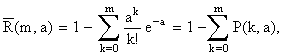(5.2.8)

которая затабулирована.

Обозначим 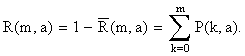С помощью этой функции можно подсчитать вероятности событий, связанных со случайной величиной X, распределённой по закону Пуассона с параметром a:

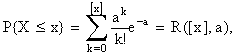
где [ x ] – целая часть числа x. Следовательно, 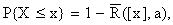откуда

Пример 2. Пусть некоторое устройство отказывает с постоянной интенсивностью l=1 (отказ/сутки). Найти вероятность того, что за двое суток: а) не будет ни одного отказа; б) будет ровно один отказ; в) будет хотя бы один отказ.

Решение. Случайная величина X – число отказов за 2 суток – распределена по закону Пуассона с параметром a= l× t =1×2=2. Имеем:

а) P₀=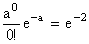; так как 0!=1, то P₀=e^-2»0,1353;

б) P₁=»2×0,1353=0,2706;

в) P{X³1}=1 – P{X=0}=1 – P₀=0,8647.

Пример 3. Поток сбоев (отказов) модемной связи можно считать простейшим с интенсивностью l=4 (сбоя/час). Найти вероятность того, что за полчаса произойдёт: а) ровно один сбой; б) хотя бы один сбой; в) не менее трёх сбоев.

Решение. t=0,5; a =4×0,5=2.

а) P₁=2×e^-2»2×0,135=0,270.

б) R₁=1-P₀»0,865.

в) R₃=1-(P₀+P₁+P₂)=1-R(2, a)=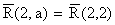»0,325.

Пример 4. Космические частицы, попадающие в спутник, образуют поле с плотностью l (частица/м²). Агрегат спутника, находящийся в поле частиц, занимает площадь S (м²). Для выхода из строя агрегата заведомо достаточно попадания в него двух частиц; при попадании одной частицы он выходит из строя с вероятностью р. Найти вероятностью события А={выход агрегата из строя}.

Решение. Находим среднее число попадающих в агрегат частиц:

а=lS.

Найдем вероятность выхода агрегата из строя по формуле полной вероятности с гипотезами:

Н₁={в агрегат попала одна частица},

Н₂={в агрегат попало не менее двух частиц}.

По закону Пуассона

Р(Н₁)= lS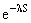; P(H₂)=R₂=1-P₀-P₁=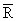(1, lS)=1-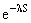(1+lS);

P(A|H₁)=p; P(A|H₂)=1;

По формуле полной вероятности

P(A)= lSp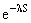+1-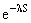(1+lS).

Пример 5. Поток отказов оборудования – пуассоновский нестационарный с интенсивностью l(t), зависящей от времени. На участке времени от 0 часов до 400 часов интенсивность l(t) возрастает по линейному закону:

l(t)= bt+c,

причём в 0 часов она равна 0,2 (отказов в час), а в 400 часов – 0,4 (отказов в час). Найти вероятность P того, что за 10 часов, от 195 часов до 205 часов, произойдёт не менее трёх отказов.

Решение. Найдём постоянные b и c: l(0)=0,2; c =0,2[отказов/час]; l(400)= b ×400+0,2=0,4 [отказов/час], откуда b =0,2/400=1/2000 [отказов/час²]. Среднее число отказов a в интервале от 195 часов до 205 часов будет

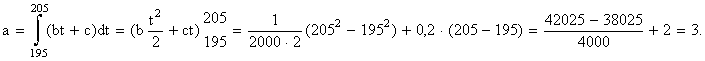
Искомая вероятность P будет

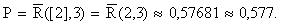
Дата добавления: 2014-01-07