Марковские случайные процессы. Уравнения Колмогорова для вероятностей состояний

Многие явления, которые приходится анализировать для определения их свойств и параметров, развиваются как случайные процессы, ход и исход которых зависят от ряда случайных факторов, сопровождающих эти явления.

Для того, чтобы вычислить числовые параметры, характеризующие подобные явления, нужно построить некоторую вероятностную модель явления, учитывающую сопровождающие его случайные факторы.

Для математического описания многих явлений, развивающихся в форме случайного процесса, может быть с успехом применен математический аппарат, разработанный в теории вероятностей для так называемых марковских случайных процессов.

Рассмотрим понятие марковского случайного процесса.

Пусть имеется некоторая физическая система S, состояние которой меняется с течением времени (под системой S может пониматься что угодно: техническое устройство, ремонтная мастерская, вычислительная машина, железнодорожный узел и т.д.). Если состояние системы S меняется во времени случайным, заранее непредсказуемым образом, мы говорим, что в системе S протекает случайный процесс.

Случайный процесс, протекающий в системе S, называется марковским процессом (или «процессом без последействия»), если он обладает следующим свойством:

Для каждого момента времени t₀ вероятность любого состояния системы в будущем (при t>t₀) зависит только от её состояния в настоящем (при t=t₀) и не зависит от того, когда и каким образом система пришла в это состояние (т.е. как развивался процесс в прошлом).

Другими словами, в марковском случайном процессе будущее развитие его зависит только от настоящего состояния и не зависит от «предыстории» процесса.

Рассмотрим пример. Пусть система S представляет собой техническое устройство, которое уже проработало некоторое время, соответственным образом «износилось» и пришло в некоторое состояние, характеризующееся определенной степенью изношенности S. Нас интересует, как будет работать система в будущем. Ясно, что, по крайней мере в первом приближении, характеристики работы системы в будущем (частота отказов, потребность в ремонте) зависят от состояния устройства в настоящий момент и не зависят от того, когда и как устройство достигло своего настоящего состояния.

На практике часто встречаются случайные процессы, которые, с той или другой степенью приближения, можно считать марковскими.

Марковские случайные процессы делятся на классы по некоторым признакам, в зависимости от того, как и в какие моменты времени система S может менять свои состояния.

Случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы:

S₁, S₂, S₃, …

можно перечислить (перенумеровать) одно за другим, а сам процесс состоит в том, что время от времени система S скачком (мгновенно) перескакивает из одного состояния в другое.

Пример. Техническое устройство S состоит из двух узлов: I и II, каждый из которых может в ходе работы устройства отказать (выйти из строя). Возможны следующие состояния системы:

S₁ – оба узла работают; S₂ – первый узел отказал, второй работает;

S₃ – второй узел отказал, первый работает; S₄ – оба узла отказали.

Процесс, протекающий в системе, состоит в том, что она случайным образом, в какие-то моменты времени, переходит (перескакивает) из состояния в состояние. Всего у системы четыре возможных состояния, которые мы перенумеровали. Перед нами – процесс с дискретными состояниями.

В данной главе мы будем рассматривать только случайные процессы с дискретными состояниями.

При анализе случайных процессов с дискретными состояниями очень удобно пользоваться геометрической схемой – так называемым графом состояний. Граф состояний геометрически изображает возможные состояния системы и её возможные переходы из состояния в состояние.

Пусть имеется система S с дискретными состояниями:

S₁, S₂, …, S_n.

Мы будем изображать каждое состояние прямоугольником, а возможные переходы («перескоки») из состояния в состояние – стрелками, соединяющими эти прямоугольники (рис.8.3.1.1).

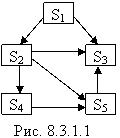
Заметим, что стрелками отмечаются только непосредственные переходы из состояния в состояние; если система может перейти из состояния S₁ в S₃ только через S₂, то стрелками отмечаются только переходы S₁®S₂ и S₂®S₃, но не S₁®S₃.

Способы математического описания марковского случайного процесса, протекающего в системе с дискретными состояниями, зависят от того, в какие моменты времени – заранее известные или случайные – могут происходить переходы («перескоки») системы из состояния в состояние.

Случайный процесс называется процессом с дискретным временем, если переходы системы из состояния в состояние возможны только в строго определенные, заранее фиксированные моменты времени: t₁, t₂, …. В промежутки времени между этими моментами система S сохраняет свое состояние.

Случайный процесс называется процессом с непрерывным временем, если переход системы из состояния в состояние возможен в любой, наперед неизвестный, случайный момент t.

На практике значительно чаще встречаются ситуации, когда переходы системы из состояния в состояние происходят не в фиксированные, а в случайные моменты времени, которые заранее указать невозможно – переход может осуществиться, вообще говоря, в любой момент. Например, выход из строя (отказ) любого элемента аппаратуры может произойти в любой момент времени; окончание ремонта (восстановление) этого элемента также может произойти в заранее не фиксированный момент и т.д.

Для описания таких процессов в ряде случаев может быть с успехом применена схема марковского случайного процесса с дискретными состояниями и непрерывным временем, который мы будем для краткости называть непрерывной цепью Маркова.

Покажем, как выражаются вероятности состояний для такого процесса.

Пусть имеется ряд дискретных состояний:

S₁, S₂, …, S_n;

переход (перескок) системы S из состояния в состояние может осуществляться в любой момент времени. Граф состояний системы представлен на рис. 8.3.1.2.

Обозначим p_i(t) – вероятность того, что в момент t система S будет находиться в состоянии S_i (i=1,…,n). Очевидно, для любого момента t сумма вероятностей состояний равна единице:

,

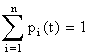так как события, состоящие в том, что в момент t система находится в состояниях S₁, S₂, …, S_n, несовместны и образуют полную группу.

Поставим задачу – определить для любого t вероятности состояний: p₁(t), p₂(t), …, p_n(t).

Для того, чтобы найти эти вероятности, необходимо знать характеристики процесса, аналогичные переходным вероятностям для марковской цепи. В случае процесса с непрерывным временем нам не придется задавать определенные, отличные от нуля, переходные вероятности P_ij; вероятность перехода (перескока) системы из состояния в состояние точно в момент t будет равна нулю (так же как вероятность любого отдельного значения непрерывной случайной величины). Вместо переходных вероятностей P_ij мы введем в рассмотрение плотности вероятностей перехода l_ij.

Пусть система S в момент t находится в состоянии S_i. Рассмотрим элементарный промежуток времени Dt, примыкающий к моменту t (рис. 8.3.1.3).

Назовем плотностью вероятности перехода l_ij предел отношения вероятности перехода системы за время Dt из состояния S_i в состояние S_j к длине промежутка Dt:

, (8.3.1.1)

где P_ij(Dt) – вероятность того, что система, находившаяся в момент t в состоянии S_i, за время Dt перейдет из него в состояние S_j (плотность вероятностей перехода определяется только для j¹i).

Из формулы (8.3.1.1) следует, что при малом Dt вероятность перехода P_ij(Dt) (с точностью до бесконечно малых высших порядков) равна l_ijDt:

P_ij(Dt)» l_ijDt.

Если все плотности вероятностей перехода l_ij не зависят от t (т.е. от того, в какой момент начинается элементарный участок Dt), марковский процесс называется однородным; если эти плотности представляют собой какие-то функции времени l_ij(t), процесс называется неоднородным. При пользовании сокращенным названием «непрерывная марковская цепь» мы также будем различать однородные и неоднородные цепи.

Предположим, что нам известны плотности вероятностей перехода l_ij для всех пар состояний S_i, S_j.

Построим граф состояний системы S и против каждой стрелки проставим соответствующую плотность вероятности перехода (рис.8.3.1.4).

Такой граф, с проставленными у стрелок плотностями вероятностей перехода, мы будем называть размеченным графом состояний.

Оказывается, зная размеченный граф состояний, можно определить вероятности состояний:

p₁(t), p₂(t), …, p_n(t) (8.3.1.2)

как функции времени. А именно, эти вероятности удовлетворяют определенного вида дифференциальным уравнениям, так называемым уравнениям Колмогорова. Решая эти уравнения, мы получим вероятности (8.3.1.2).

Продемонстрируем методику вывода уравнений Колмогорова для вероятностей состояний на конкретном примере.

Пусть система S имеет четыре возможных состояния: S₁, S₂, S₃, S₄; размеченный граф состояний системы показан на рис.8.3.1.4.

Поставим себе задачу: найти одну из вероятностей состояний, например, p₁(t). Это есть вероятность того, что в момент t система будет находиться в состоянии S₁.

Как это событие может произойти? Очевидно, двумя способами:

1) в момент t система уже была в состоянии S₁, а за время Dt не вышла из этого состояния;

2) в момент t система была в состоянии S₃, а за время Dt перешла из него в S₁.

Вероятность первого варианта найдем как произведение вероятности p₁(t) того, что в момент t система была в состоянии S₁, на условную вероятность того, что будучи в состоянии S₁, система за время Dt не перейдет из него в S₂. Эта условная вероятность (с точностью до бесконечно малых высших порядков) равна 1-l₁₂Dt.

Аналогично, вероятность второго варианта равна вероятности того, что в момент t система была в состоянии S₃, умноженной на условную вероятность перехода за время Dt в состояние S₁:

p₃(t)l₃₁Dt.

Применяя правило сложения вероятностей, получим:

p₁(t+Dt)=p₁(t)(1-l₁₂Dt)+p₃(t)l₃₁Dt.

Раскроем скобки в правой части, перенесем p₁(t) в левую и разделим обе части равенства на Dt; получим:

.

Теперь устремим Dt к нулю и перейдем к пределу:

.

Левая часть есть не что иное, как производная функции p₁(t):

. (8.3.1.3)

Таким образом, выведено дифференциальное уравнение, которому должна удовлетворять функция p₁(t). Аналогичные дифференциальные уравнения могут быть выведены и для остальных вероятностей состояния: p₂(t), p₃(t), p₄(t).

Рассмотрим второе состояние S₂ и найдем p₂(t+Dt), - вероятность того, что в момент (t+Dt) система S будет находиться в состоянии S₂. Это событие может произойти следующими способами:

- в момент t система уже была в состоянии S₂, а за время Dt не перешла ни в S₃, ни в S₄;

- в момент t система была в состоянии S₁, а за время Dt перешла из него в S₂;

- в момент t система была в состоянии S₄, а за время Dt перешла из него в S₂.

Вероятность первого варианта вычисляется так: p₂(t) умножается на условную вероятность того, что система за Dt не перейдет ни в S₃, ни в S₄. Так как события, состоящие в переходе за время Dt из S₂ в S₃ и из S₂ в S₄, несовместны, то вероятность того, что осуществится один из этих переходов, равна сумме их вероятностей, т.е. l₂₃Dt+l₂₄Dt (с точностью до бесконечно малых высших порядков). Вероятность того, что не осуществится ни один из этих переходов, равна 1-l₂₃Dt-l₂₄Dt. Отсюда вероятность первого варианта:

p₂(t)(1-l₂₃Dt-l₂₄Dt).

Прибавляя сюда вероятности второго и третьего вариантов, получим:

p₂(t+Dt)= p₂(t)(1-l₂₃Dt-l₂₄Dt)+ p₁(t)l₁₂Dt+ p₄(t)l₄₂Dt.

Перенося p₂(t) в левую часть, деля на Dt и переходя к пределу, получим дифференциальное уравнение для p₂(t):

. (8.3.1.4)

Рассуждая аналогично для состояний S₃, S₄, получим в результате систему дифференциальных уравнений, составленных по типу (8.3.1.3) и (8.3.1.4). Отбросим в них для краткости аргумент t у функций р₁, р₂, р₃, р₄ и перепишем эту систему в виде:

(8.3.1.5)

Эти уравнения для вероятностей состояний и называются уравнениями Колмогорова.

Интегрирование этой системы уравнений даст нам искомые вероятности состояний как функции времени. Начальные условия берутся в зависимости от того, каково было начальное состояние системы S. Например, если в начальный момент времени (при t=0) система S находилась в состоянии S₁, то надо принять начальные условия:

при t=0 p₁=1, p₂=p₃=p₄=0.

Заметим, что всех четырех уравнений для p₁, p₂, p₃, p₄ можно было бы и не писать; действительно, p₁+p₂+p₃+p₄=1 для всех t, и любую из вероятностей p₁, p₂, p₃, p₄ можно выразить через три остальные. Например, p₄ можно выразить через p₁, p₂, p₃ в виде

p₄=1-(p₁+p₂+p₃)

и подставить в остальные уравнения. Тогда специального уравнения для вероятности р₄ можно и не писать. Однако иногда в дальнейшем нам может быть удобнее пользоваться полной системой уравнений типа (8.3.1.5).

Обратим внимание на структуру уравнений (8.3.1.5). Все они построены по вполне определенному правилу, которое можно сформулировать следующим образом.

В левой части каждого уравнения стоит производная вероятности состояния, а правая часть содержит столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния, соответствующий член имеет знак «минус»; если в состояние – знак «плюс». Каждый член равен произведению плотности вероятности перехода, соответствующей данной стрелке, умноженной на вероятность того состояния, из которого исходит стрелка.

Это правило составления дифференциальных уравнений для вероятностей состояний является общим и справедливо для любой непрерывной марковской цепи; с его помощью можно совершенно механически, без всяких рассуждений, записывать дифференциальные уравнения для вероятностей состояний непосредственно по размеченному графу состояний.

8.3. Надёжность резервированной системы (продолжение)

Задача 2. Система с холодным резервом и простейшими потоками отказов. Резервированная система (блок) S состоит из основного элемента Э1 и двух резервных: Э2, Э3. При отказе элемента Э1 в работу включается Э2, при отказе Э2 - Э3, (рис.8.3.3).

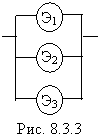
До включения каждый из резервных элементов находится в «холодном» резерве и отказать не может. Интенсивность потока отказов основного элемента l₁; интенсивность потока отказов каждого из резервных элементов, когда они работают, одинакова и равна l₂. Все потоки отказов простейшие. Требуется определить надежность системы S.

Представим процесс, протекающий в системе S, как марковский случайный процесс с непрерывным временем и с дискретными состояниями:

S₁ – работает основной элемент Э₁,

S₂ – работает резервный элемент Э₂,

S₃ – работает резервный элемент Э₃,

S₄ - не работает ни один элемент.

Граф состояний системы показан на рис. 8.3.4. Так как восстановления элементов не происходит, все стрелки на графе ведут в одну сторону.

Система уравнений Колмогорова для вероятностей состояний будет:

(8.3.8)

К ним надо прибавить нормировочное условие:

p₁ + p₂ + p₃+ p₄ =1. (8.3.9)

Из первого уравнения выражаем p₁ как функцию t:

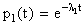(8.3.10)

(начальное условие, при котором мы проинтегрировали это уравнение, p₁(0) = 1). Подставляя (8.3.10) во второе уравнение, получим:

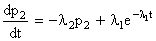. (8.3.11)

Проинтегрируем это уравнение с начальным условием p₂(0)=0; получим:

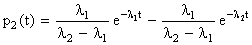. (8.3.12)

Эту функцию подставим в третье уравнение (8.3.8); получим:

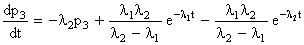(8.3.13)

Уравнение (8.3.13) нужно проинтегрировать тоже при начальном условии p₃(0)=0; получим:

(8.3.14)

Для нахождения функции р₄(t) не нужно интегрировать последнее уравнение (8.3.8) – ее можно найти из условия (8.3.9):

.►

Задача 3. Система с облегченным резервом и простейшими потоками отказов. Резервированная система (блок) S состоит из основного элемента Э₁ и трех резервных: Э₂, Э₃, Э₄ (рис. 8.3.5). Основной элемент подвергается простейшему потоку отказов с интенсивностью l₁; каждый из резервных до своего включения подвергается потоку отказов с интенсивностью l₂; после включения резервного элемента эта интенсивность мгновенно подскакивает до значения ₂. При отказе основного элемента Э₁ включается в работу резервный Э₂, при отказе Э₂ – Э₃ и т.д.

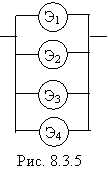
Требуется определить надежность системы.

Будем нумеровать состояние системы двумя индексами: первый равен единице, если основной элемент работает, и нулю – если не работает; второй равен числу исправных резервных элементов:

S₁₃ - основной элемент исправен (работает), все три резервных исправны;

S₁₂ - основной элемент исправен (работает), из трех резервных один отказал, два исправны;

S₁₁ - основной элемент исправен (работает), из трех резервных два отказали, один исправен;

S₁₀ - основной элемент исправен (работает), все три резервных отказали;

S₀₃ - основной элемент отказал, работает один из резервных, остальные два исправны;

S₀₂ - основной элемент отказал, работает один из резервных, из остальных резервных один исправен, другой отказал;

S₀₁ - основной элемент отказал, работает один из резервных, остальные два резервных отказали;

S ₀₀– все элементы отказали.

Граф состояний системы показан на рис.8.3.6.

Система уравнений Колмогорова для вероятностей состояний имеет вид:

(8.3.15)

К этим уравнениям нужно добавить условие:

p₁₃ + p₁₂ + p ₁₁+ p₁₀ + p₀₃ + p₀₂ + p₀₁ + p₀₀ =1,

позволяющее отбросить любое из уравнений (6.15).

Интегрирование системы (8.3.15) может быть осуществлено в следующем порядке: из первого уравнения находим p₁₃(t):

. (8.3.16)

Это выражение подставляется во второе уравнение, которое теперь содержит только одну неизвестную функцию p₁₂(t); находим ее, подставляем в третье уравнение, и так далее. На каждом шаге такого процесса новые функции мы выражаем через уже известные, пока, наконец, не доходим до p₀₀, которую выражаем через все остальные:

p₀₀(t)=1-(p₁₃(t)+p₁₂(t)+p₁₁(t)+ p₁₀(t)+ p₀₃(t)+ p₀₂(t)+ p₀₁(t)).

После того, как вычисления произведены и функции p₁₃(t),…,p₀₀(t) найдены, можно найти надежность системы P(t). Очевидно, она равна сумме вероятностей всех состояний, при которых система работает:

P(t)=p₁₃(t)+p₁₂(t)+p₁₁(t)+ p₁₀(t)+ p₀₃(t)+ p₀₂(t)+ p₀₁(t),

или, что то же P(t)=1-p₀₀(t).►

Дата добавления: 2014-01-07