
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Критерии надежности восстанавливаемых изделий
|
|
|
|
Как уже отмечалось, на практике зачастую неизвестны функциональные зависимости, описывающие надёжность, плотность распределения и другие характеристики надёжности интересующих нас устройств. Поэтому соответствующие показатели надёжности определяются по данным экспериментальных наблюдений. Так же отмечалось, что на практике (особенно в технике) часто используются другие названия этих характеристик.
Помимо показателей надёжности, используемых для невосстанавливаемых изделий (вероятность безотказной работы P(t); частота отказов a(t); интенсивность отказов l(t); средняя наработка до первого отказа Tср), для восстанавливаемых изделий применяются следующие показатели:
- наработка на отказ tср;
- параметр потока отказов w(t);
- функция готовности Кг(t);
- коэффициент готовности Кг.
Познакомимся, как они определяются в практической деятельности.
Рассмотрим следующую модель испытания.
Пусть на испытании находится N изделий и пусть отказавшие изделия немедленно заменяются исправными (новыми или отремонтированными). Испытания считаются законченными, если число отказов достигает величины, достаточной для оценки надежности с определенной доверительной вероятностью. Если не учитывать времени, потребного на восстановление системы, то количественными характеристиками надежности могут быть параметр потока отказов w(t) и наработка на отказ tср.
Параметром потока отказов называется отношение числа отказавших изделий в единицу времени к числу испытываемых изделий при условии, что все вышедшие из строя изделия заменяются исправными (новыми или отремонтированными). Согласно определению
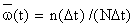 , (8.4.1.1)
, (8.4.1.1)
где n(Dt) – число отказавших образцов в интервале времени от t-Dt/2 до t+Dt/2; N – число испытываемых образцов; Dt – интервал времени.
|
|
|
Выражение (8.4.1.1) является статистическим определением параметра потока отказов.
Параметр потока отказов и частота отказов для ординарных потоков с ограниченным последействием связаны интегральным уравнением Вольтерра второго рода
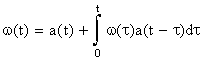 . (8.4.1.2)
. (8.4.1.2)
По известной а(t) можно найти все количественные характеристики надежности невосстанавливаемых изделий. Поэтому (8.4.1.2) является основным уравнением, связывающим количественные характеристики надежности невосстанавливаемых и восстанавливаемых изделий при мгновенном восстановлении.
Уравнение (8.4.1.2) можно записать в операторной форме:

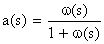 . (8.4.1.3)
. (8.4.1.3)
Соотношения (8.4.1.3) позволяют найти одну характеристику через другую, если существуют преобразования Лапласа функций а(s) и w(s) и обратные преобразования выражений (8.4.1.3).
Параметр потока отказов обладает следующими важными свойствами:
1) для любого момента времени независимо от закона распределения времени безотказной работы параметр потока отказов больше, чем частота отказов, т.е. w(t)>a(t);
2) независимо от вида функции a(t) параметр потока отказов w(t) при t®¥ стремится к 1/Тср. Это важное свойство параметра потока отказов означает, что при длительной эксплуатации ремонтируемого изделия поток его отказов независимо от закона распределения времени безотказной работы становится стационарным. Однако это вовсе не означает, что интенсивность отказов есть величина постоянная;
3) если l(t) – возрастающая функция времени, то l(t)>w(t)>a(t), если l(t) – убывающая функция, то w(t)>l(t)>a(t);
4) при l(t)¹const параметр потока отказов системы не равен сумме параметров потоков отказов элементов, т.е. 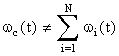 . (8.4.1.4)
. (8.4.1.4)
Это свойство параметра потока отказов позволяет утверждать, что при вычислении количественных характеристик надежности сложной системы нельзя суммировать имеющиеся в настоящее время значения интенсивностей отказов элементов, полученные по статистическим данным об отказах изделий в условиях эксплуатации, так как указанные величины являются фактически параметрами потока отказов;
|
|
|
5) при l(t)=l=const параметр потока отказов равен интенсивности отказов w(t)=l(t)=l.
Из рассмотрения свойств интенсивности и параметра потока отказов видно, что эти характеристики различны.
В настоящее время широко используются статистические данные об отказах, полученные в условиях эксплуатации аппаратуры. При этом они часто обрабатываются таким образом, что приводимые характеристики надежности являются не интенсивностью отказов, а параметром потока отказов w(t). Это вносит ошибки при расчетах надежности. В ряде случаев они могут быть значительными.
Для получения интенсивности отказов элементов из статистических данных об отказах ремонтируемых систем необходимо воспользоваться формулой (3.16) (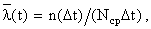 где Nср=(Ni+Ni+1)/2 – среднее число исправно работающих изделий в интервале Dt), для чего необходимо знать предысторию каждого элемента принципиальной схемы. Это может существенно усложнить методику сбора статистических данных об отказах. Поэтому целесообразно определять l(t) по параметру потока отказов w(t). Методика расчета сводится к следующим вычислительным операциям:
где Nср=(Ni+Ni+1)/2 – среднее число исправно работающих изделий в интервале Dt), для чего необходимо знать предысторию каждого элемента принципиальной схемы. Это может существенно усложнить методику сбора статистических данных об отказах. Поэтому целесообразно определять l(t) по параметру потока отказов w(t). Методика расчета сводится к следующим вычислительным операциям:
- по статистическим данным об отказах элементов ремонтируемых изделий и по формуле (8.4.1.1) вычисляется параметр потока отказов и строится гистограмма wi(t);
- гистограмма заменяется кривой, которая аппроксимируется уравнением;
- находится преобразование Лапласа wi(s) функции wi(t);
- по известной wi(s) на основании (8.4.1.3) записывается преобразование Лапласа аi(s) частоты отказов;
- по известной аi(s) находится обратное преобразование частоты отказов аi(t);
- находится аналитическое выражение для интенсивности отказов по формуле
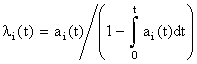 ; (8.4.1.5)
; (8.4.1.5)
- строится график li(t).
Если имеется участок, где li(t)= li=const, то постоянное значение интенсивности отказов принимается для оценки вероятности безотказной работы. При этом считается справедливым экспоненциальный закон надежности.
Приведенная методика не может быть применена, если не удается найти по а(s) обратное преобразование частоты отказов а(t). В этом случае приходится применять приближенные методы решения интегрального уравнения (8.4.1.2). Решение наиболее просто можно получить с помощью ЭЦВМ.
|
|
|
Наработкой на отказ называется среднее значение времени между соседними отказами.
Эта характеристика определяется по статистическим данным об отказах по формуле
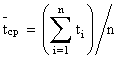 , (8.4.1.6)
, (8.4.1.6)
где ti – время исправной работы изделия между (i-1)-м и i-м отказами; n – число отказов за некоторое время t.
Из формулы (8.4.1.6) видно, что в данном случае наработка на отказ определяется по данным испытания одного образца изделия. Если на испытании находится N образцов в течение времени t, то наработка на отказ вычисляется по формуле
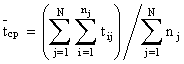 , (8.4.1.7)
, (8.4.1.7)
где tij – время исправной работы j-го образца изделия между (i-1)-м и i-м отказом; nj – число отказов за время t j-го образца.
Наработка на отказ является достаточно наглядной характеристикой надежности, поэтому она получила широкое распространение на практике.
Параметр потока отказов и наработка на отказ характеризуют надежность ремонтируемого изделия и не учитывают времени, потребного на его восстановление. Поэтому они не характеризуют готовности изделия к выполнению своих функций в нужное время. Для этой цели вводится такие критерии, как коэффициент готовности и коэффициент вынужденного простоя.
Коэффициентом готовности называется отношение времени исправной работы к сумме времен исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок. Эта характеристика обозначается Кг.
Согласно данному определению
Кг=tp/(tp+tп), (8.4.1.8)
где tp – суммарное время исправной работы изделия; tп – суммарное время вынужденного простоя.
Времена tp и tп вычисляются по формулам
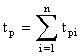 ,
, 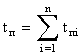 , (8.4.1.9)
, (8.4.1.9)
где tpi – время работы изделия между (i-1)-м и i-м отказом; tпi – время вынужденного простоя после i-го отказа; n – число отказов (ремонтов) изделия.
Выражение (8.4.1.8) является статистическим определением коэффициента готовности. Для перехода к вероятностной трактовке величины tp и tп заменяются математическими ожиданиями времени между соседними отказами и времени восстановления соответственно.
|
|
|
Тогда
Кг=tср/(tср+tв) (8.4.1.10)
где tср – наработка на отказ; tв – среднее время восстановления.
Коэффициентом вынужденного простоя называется отношение времени вынужденного простоя к сумме времен исправной работы и вынужденных простоев изделия, взятых за один и тот же календарный срок.
Согласно определению
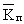 =tп/(tр+tп) (8.4.1.11)
=tп/(tр+tп) (8.4.1.11)
или, переходя к средним величинам,
Кп=tв/(tср+tв). (8.4.1.12)
Коэффициент готовности и коэффициент вынужденного простоя связаны между собой зависимостью
Кп=1-Кг. (8.4.1.13)
При анализе надежности восстанавливаемых систем обычно коэффициент готовности вычисляют по формуле
Кг=Тср/(Тср+tв). (8.4.1.14)
Однако формула (8.4.1.14) верна только в том случае, если поток отказов простейший, и тогда tср=Тср.
Часто коэффициент готовности, вычисленный по формуле (8.4.1.14), отождествляют с вероятностью того, что в любой момент времени восстанавливаемая система исправна. На самом деле указанные характеристики неравноценны и могут быть отождествлены при определенных допущениях.
Действительно, вероятность возникновения отказа ремонтируемой системы в начале эксплуатация мала. С ростом времени t эта вероятность возрастает. Это означает, что вероятность застать систему в исправном состоянии в начале эксплуатации будет выше, чем по истечении некоторого времени. Между тем на основании формулы (8.4.1.14) коэффициент готовности не зависит от времени работы.
Для выяснения физического смысла коэффициента готовности Кг запишем формулу для вероятности застать систему в исправном состоянии. При этом рассмотрим наиболее простой случай, когда интенсивность отказов и интенсивность восстановления есть величины постоянные.
Предполагая, что при t=0 система находится в исправном состоянии (Р(0)=1), вероятность застать систему в исправном состоянии определяется из выражений
 ,
,
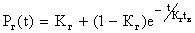 , (8.4.1.15)
, (8.4.1.15)
где 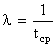 ;
;  ;
; 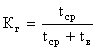 .
.
Это выражение устанавливает зависимость между коэффициентом готовности системы и вероятностью застать её в исправном состоянии в любой момент времени t.
Из (8.4.1.15) видно, что Рг(t)®Кг при t®¥, т.е. практически коэффициент готовности имеет смысл вероятности застать изделие в исправном состоянии при установившемся процессе эксплуатации.
В некоторых случаях критериями надежности восстанавливаемых систем могут быть также критерии надежности невосстанавливаемых систем, например: вероятность безотказной работы, частота отказов, средняя наработка до первого отказа, интенсивность отказов. Такая необходимость возникает всегда, когда имеет смысл оценить надежность восстанавливаемой системы до первого отказа, а также в случае, когда применяется резервирование с восстановлением отказавших резервных устройств в процессе работы системы, причем отказ всей резервированной системы не допускается.
Пример 1. В течение некоторого периода времени производилось наблюдение за работой одного экземпляра радиолокационной станции. За весь период наблюдения было зарегистрировано 15 отказов. До начала наблюдения станция проработала 258 часов, к концу наблюдения наработка станции составила 1233 час. Требуется определить среднюю наработку на отказ tср.
Решение. 1. Наработка радиолокационной станции за наблюдаемый период равна
t=t2-t1=1233-258=975 час.
2. Принимая 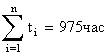 , по формуле (8.4.1.6) находим среднюю наработку на отказ:
, по формуле (8.4.1.6) находим среднюю наработку на отказ:
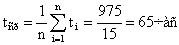 .►
.►
Пример 2. Производилось наблюдение за работой трех экземпляров однотипной аппаратуры. За период наблюдения было зафиксировано по первому экземпляру аппаратуры 6 отказов, по второму и третьему – 11 и 8 отказов соответственно. Наработка первого экземпляра составила 181 час, второго – 329 и третьего – 245 час. Требуется определить наработку аппаратуры на отказ.
Решение. 1. Определяем суммарную наработку трех образцов аппаратуры:
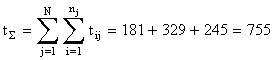 час.
час.
2. Определяем суммарное количество отказов: 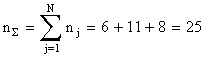 отказов.
отказов.
3. Находим среднюю наработку на отказ по формуле (8.4.1.7):
 час.►
час.►
Пример 3. Система состоит из 5 приборов, причем отказ любого одного из них ведет к отказу системы. Известно, что первый прибор отказал 34 раза в течение 952 час. работы, второй – 24 раза в течение 960 час. работы, а остальные приборы в течение 210 час. работы отказали 4, 6 и 5 раз соответственно. Требуется определить наработку на отказ системы в целом, если справедлив экспоненциальный закон надежности для каждого из пяти приборов.
Решение. Для решения данной задачи воспользуемся следующими соотношениями:
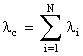 и
и 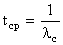 .
.
1. Определим интенсивность отказов для каждого прибора:
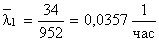 ,
, 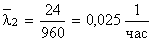 ,
, 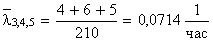 .
.
2. Интенсивность отказов системы будет
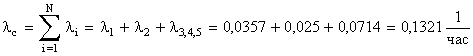 .
.
3. Средняя наработка на отказ системы равна 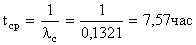 .►
.►
8.5. Учёт зависимости отказов при оценке надёжности технических устройств
До сих пор, анализируя надежность технических устройств (систем), составленных из элементов, мы предполагали, что отказы этих элементов происходят независимо друг от друга. Это допущение не всегда справедливо: в ряде случаев отказы элементов могут быть зависимыми.
Зависимость между отказами может быть двух типов:
1. Отказ какого-либо элемента меняет режим работы системы (например, может возникнуть короткое замыкание или резкие колебания напряжения; или же выход из строя одного элемента, являющегося регулятором, меняет режим работы других).
2. На всю совокупность элементов действует какой-то один случайный фактор (температура, вибрация и т. д.), одновременно влияющий на надежность всех элементов или части из них.
Остановимся вкратце на способах учета обоих типов зависимости.
Пусть имеется налицо зависимость отказов первого типа - выход из строя одного элемента влияет на режим работы и, значит, на надежность остальных. Очевидно, если мы имеем дело с простой (нерезервированной) системой при отсутствии восстановления, то зависимость первого типа не может сказаться на надежности системы. Если же система резервирована (или происходит восстановление), зависимость такого типа должна учитываться.
Пример 1. Система состоит из двух элементов: основного Э1 и резервного Э2, работающего в «горячем резерве» (рис.8.5.1). При отказе основного элемента система автоматически переключается на резервный элемент. Интенсивность потока отказов обоих элементов в нормальном рабочем состоянии одинакова и равна l. Выход из строя основного элемента влияет на режим работы резервного так, что интенсивность отказов l увеличивается на величину f(t-t1), где t1 - момент отказа основного элемента.

Таким образом, условная интенсивность отказов резервного элемента при условии, что основной отказал в момент t1, равна:
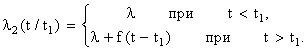
Требуется определить надежность системы P(t)
Решение. Данная задача сводится к уже решенной ранее. Действительно, полагая l1(t)=l2(t)=l;  (t/t1)=l+f(t-t1), мы приходим к той схеме, которая рассматривалась в задаче 1 параграфа 8.3 («облегчённый» резерв).►
(t/t1)=l+f(t-t1), мы приходим к той схеме, которая рассматривалась в задаче 1 параграфа 8.3 («облегчённый» резерв).►
Первый тип зависимости отказов (влияние отказов одних элементов на надежность других) наблюдается и тогда, когда некоторые элементы (регуляторы) предназначены для поддержания нормального режима работы других.
Пример 2. Система S состоит из двух «параллельно» включенных элементов: основного Э1 и резервного Э2 находящегося в облегченном резерве (рис. 8.5.2). Регулятор Эр предназначен для того, чтобы поддерживать нормальный режим работы обоих элементов: Э1 и Э2. В нормальном режиме интенсивности отказов работающего и неработающего (исправного) элементов равны соответственно l1 и l2. При отказе регулятора эти интенсивности мгновенно увеличиваются и становятся равными 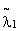 и
и  . Интенсивность потока отказов самого регулятора равна lр. Все потоки событий - простейшие. Определить надежности системы.
. Интенсивность потока отказов самого регулятора равна lр. Все потоки событий - простейшие. Определить надежности системы.
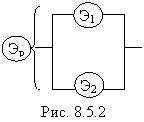
Решение. При постоянных интенсивностях отказов процесс, происходящий в системе, - марковский. Будем нумеровать состояния системы тремя индексами: первый равен нулю, если исправен регулятор и равен единице, если он вышел из строя. Второй индекс равен нулю, если исправен основной элемент Э1 и единице, если он вышел из строя. Третий индекс - то же для резервного элемента Э2.
Состояния системы (рис.8.5.3):
S000 - все три элемента исправны;
S010 - регулятор исправен, элемент Э1 вышел из строя, работает Э2;
S001 - регулятор исправен, элемент Э1 исправен, работает; Э2 вышел из строя;
S011 - регулятор исправен, оба элемента Э1 и Э2 вышли из строя;
S100 - регулятор вышел из строя; оба элемента Э1 и Э2 исправны, из них Э1 работает;
S110 - регулятор вышел из строя, элемент Э1 вышел из строя, работает Э2;
S101 - регулятор вышел из строя, элемент Э1 работает, Э2 вышел из строя;
S111- все три элемента вышли из строя.
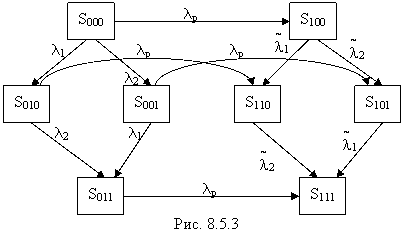
Составим по этому графу систему дифференциальных уравнений (сделайте это сами) и решив эти уравнения при начальных условиях:
t = 0; p000 = 1; p010 = … = p111 = 0,
получим вероятности состояний. Надежность системы P(t) выразится как сумма вероятностей всех состояний, кроме S011 и S111, в которых не работает ни один из элементов Э1 и Э2:
P(t) = 1 – p011(t) – p111(t). (8.5.1)
Остановимся теперь на втором типе зависимости между отказами. Этот тип зависимости обусловлен наличием каких-то случайных факторов, влияющих одновременно на работу всех элементов. Будем считать, что факторы определяют тот или иной режим работы системы. Рассмотрим сначала самый простой случай, когда режим работы системы не меняется в ходе ее эксплуатации, а остается постоянным. Так, например, можно считать, что метеорологические условия не меняются или мало меняются в процессе полета ракеты класса "Земля - Земля".
Пусть возможны несколько режимов работы: R1, R2, …, Rk
с вероятностями, равными соответственно P(R1), P(R2), …, P(Rk).
Имеется некоторая система S, надежность которой зависит от режима, при котором она работает. Обозначим условную надежность системы при i-м режиме (Ri)
P(t/Ri) (i =1, …, k).
Найдем теперь полную (безусловную) надежность системы P(t). По формуле полной вероятности:
P(t) = P(R1) P(t/R1) + P(R2) P(t/R2) + … + P(Rk) P(t/Rk),
или, короче P(t) = P(t/Ri). (8.5.2)
P(t/Ri). (8.5.2)
Пример 3. Система S состоит из двух "последовательно" соединенных элементов Э1 и Э2 и может работать в одном из трех режимов: R1, R2, R3, вероятности которых P(R1) = 0,4; P(R2) = 0,3; P(R3) = 0,3.
При режиме R1 интенсивности потоков отказов элементов Э1 и Э2 равны 0,1 и 0,2 (отказов в час), при режиме R2 они равны 0,3 и 0,4, при режиме R3 - 0,4 и 0,5. Определить надежность системы и вычислить ее для t=2 час.
Решение. При "последовательном" соединении элементов интенсивности отказов складываются. Находим условные надежности системы при трех режимах:
P(t/R1) = e-(0,1+0,2)t = e-0,3t,
P(t/R2) = e-(0,3+0,4)t = e-0,7t,
P(t/R3) = e-(0,4+0,5)t = e-0,9t.
Отсюда P(t) = 0,4e-0,3t +0,3e-0,7t +0,3e-0,9t .
Полагая t = 2, получим: P(2) = 0,4e-0,6 - 0,3e-1,4 + 0,3e-1,8 = 0,4× 0,549 – 0,3× 0,247 – 0,3× 0,165 = 0,343. ►
Аналогично рассмотренной дискретной схеме нескольких режимов можно определить надежность системы, если режим работы характеризуется некоторой непрерывной случайной величиной R (скажем, температурой), имеющей известную плотность распределения f(r). Тогда в формуле (8.5.2) вместо суммы будет фигурировать интеграл:
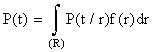 , (8.5.3)
, (8.5.3)
где P(t/r)- условная надежность системы при условии, что R=r; f(r) - плотность распределения параметра R.
Интеграл распространяется на всю область (R) возможных значений параметра R.
Пример 4. Система S состоит из двух элементов Э1, Э2, включенных «параллельно»; резервный элемент Э2 находится в «горячем» резерве. Интенсивность потока отказов каждого элемента постоянна во времени, но зависит от режима работы системы - температуры (θ); эта зависимость выражается формулой l(θ)=l0+a θ.
Плотность распределения температуры элемента θ постоянна на интервале от J1 до J2:
f(J) = 1/(J 2 - J 1) при J 1<J <J 2.
Определить надёжность системы.
Решение. Определяем условную надёжность системы при заданном значении θ=J:
P(t/J) = 1 – (1-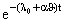 )2.
)2.
По формуле (8.5.3)

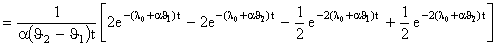 .
.
Заметим, что неучёт зависимости отказов, если она имеется и существенна, может привести к большим ошибкам, особенно, если система состоит из многих элементов.
Пример 5. Система S состоит из 50 однородных элементов, соединённых «последовательно», и может работать в одном из двух режимов:
R1-нормальном,
R2-ненормальном.
Вероятности этих режимов равны соответственно: P(R1) = 0,9; P(R2) = 0,1.
В нормальном режиме надёжность каждого элемента (за определённое время r) равна p=0,998, в ненормальном p’=0,9. Определить полную надёжность системы S и сравнить с той, которая получилась бы, если бы элементы выходили из строя независимо.
Решение. Условная надёжность системы при первом режиме: 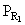 = 0,99850» 0,904;
= 0,99850» 0,904;
при втором:  = 0,950» 0,004.
= 0,950» 0,004.
Полная надёжность системы: P» 0,9× 0,904 + 0,1× 0,004 = 0,814.
Подсчитаем ту же надёжность, считая отказы элементов независимыми и приписывая каждому из них надёжность, равную 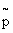 = 0,9p + 0,1p’ = 0,9882.
= 0,9p + 0,1p’ = 0,9882.
Перемножая надёжности 50 элементов, получим 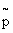 = 0,988250» 0,552. ►
= 0,988250» 0,552. ►
Как видно из примера, пренебрежение зависимостью отказов при «последовательном» соединении элементов может привести к существенному занижению надёжности. При «параллельном» соединении элементов тот же неучёт зависимости приводит не к занижению надёжности, а, наоборот, к её завышению.
Пример 6. Резервированная система состоит из основного элемента Э1 и трех резервных: Э2, Э3, Э4, работающих в «горячем» резерве. Система может работать в одном из двух режимов: R1 - нормальном и R2 - ненормальном с вероятностями Р(R1)=0.7 и Р(R2)=0.3 соответственно.
Надежность всех элементов одинакова. В нормальном режиме она равна p=0,99, в ненормальном p’=0,4. Определить полную надежность системы P и сравнить ее с той 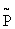 , которая получится, если считать отказы независимыми
, которая получится, если считать отказы независимыми
Решение. Условная надежность системы при каждом режиме:
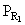 = 1 – (1 – 0,99)4» 1,000,
= 1 – (1 – 0,99)4» 1,000,  =1 – (1 – 0,4)4» 0,870.
=1 – (1 – 0,4)4» 0,870.
Полная надежность системы: P» 0,7× 1,000 + 0,3× 0,870» 0,961.
Если считать отказы элементов независимыми и приписать каждому из них надежность
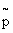 = 0,7× 0,99 + 0,3× 0,4» 0,813,
= 0,7× 0,99 + 0,3× 0,4» 0,813,
то надежность системы будет другая: 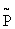 = 1 – (1 -
= 1 – (1 -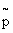 )4» 0,999,
)4» 0,999,
т.е. значительно выше, чем истинная надежность 0,961.
Завышение надежности резервированного блока, которое получается при пренебрежении зависимостью отказов, тем больше, чем больше число резервных элементов.
Если техническая система состоит из элементов, соединенных как «последовательно», так и «параллельно» (например, если дублированы только наиболее важные узлы), то пренебрежение зависимостью отказов может приводить как к завышению, так и к занижению надежности.
Наконец, рассмотрим случай, когда в процессе работы системы режим может меняться случайным образом.
Пример 7. Система S, состоящая из двух «последовательно» соединенных элементов, может работать в одном из двух режимов: R1 и R2. Переход системы из режима R1 в режим R2 происходит под действием простейшего потока событий с интенсивностью l12; обратный переход - под действием простейшего потока событий с интенсивностью l21. В режиме R1 интенсивность потока отказов первого элемента равна 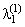 , второго -
, второго - 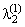 ; в режиме R2 эти интенсивности равны
; в режиме R2 эти интенсивности равны 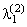 ,
, 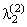 . Все потоки - простейшие. Определить надежность системы P(t).
. Все потоки - простейшие. Определить надежность системы P(t).
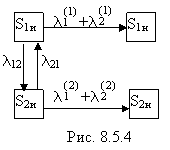
Решение. Состояния системы будут:
S1и - режим R1, оба элемента исправны;
S1н - режим R1, хотя бы один элемент неисправен;
S2и - режим R2, оба элемента исправны;
S2н - режим R2, хотя бы один элемент неисправен.
Граф состояний системы показан на рис. 8.5.4. Стрелки, переводящие систему из состояния S1н в S2н и обратно, не показаны, так как, если система неисправна, нам все равно, какой режим имеет место.
Уравнения Колмогорова для вероятностей состояний будут:
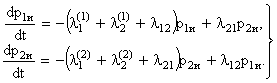 (8.5.4)
(8.5.4)
Другие вероятности нас в данном случае не интересуют, так как они соответствуют неисправной (неработающей) системе.
Если мы знаем, в каком режиме (R1 или R2) система начинает работу, то уравнения (8.5.4) будут интегрироваться при вполне определенных начальных условиях. Например, если система начинает работу в режиме R1, начальные условия будут:
t = 0, p1и = 1, p2и = 0. (8.5.5)
Проинтегрируем систему (8.5.4) например, при численных значениях параметров:
l12=1, l21=3, 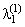 =1,
=1, 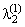 =2,
=2, 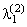 =2,
=2, 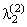 =4.
=4.
Уравнения (8.5.4) примут вид:
 (8.5.6)
(8.5.6)
Прежде всего найдем, при каких l пара функций Се-lt, Dе-lt может удовлетворять уравнениям. Подстановка такой пары в систему (8.5.6) дает:
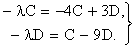
или
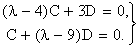 (8.5.7)
(8.5.7)
Чтобы система уравнений (8.5.7) имела какое-нибудь решение (C, D), кроме нулевого, необходимо и достаточно, чтобы был равен нулю определитель из коэффициентов этой системы:
(l - 4) (l - 9) – 1× 3 = 0
или l2 - 13 + 33 = 0.
Решая это уравнение, находим два значения l:
l 1 = 6,5 –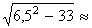 3,459,
3,459,
l 2 = 6,5 + 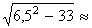 9,541.
9,541.
при значении l = l1 решение системы (8.5.7) дается формулой
D(1) = 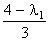 C(1) = 0,180 C(1),
C(1) = 0,180 C(1),
при значении l = l2 - формулой
D(2) = 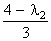 C(2) = -1,847 C(2),
C(2) = -1,847 C(2),
Отсюда вытекает, что общий вид решения системы дифференциальных уравнений (8.5.7) - пара функций: p1и(t) = C(1) e-3,459t + C(2) e-9,541t,
p2и(t) = 0,180× C(1) e-3,459t - 1,847× C(2) e-9,541t.
Начальным условиям мы можем удовлетворить соответствующим выбором произвольных постоянных С(1) и С(2). Для того чтобы выполнялось условие p1и(0)=1, p2и(0)=0, нужно, чтобы было
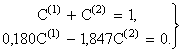
Из второго уравнения С(2) =0,097С(1); подставляя это в первое, получаем:
C(1) = 1/1,097 = 0.912; C(2) =0,088.
Окончательно p1и(t) = 0,912× e-3,459t + 0,088× e-9,541t,
p2и(t) = 0,164× (e-3,459t - e-9,541t).
Надежность системы, очевидно, будет равна сумме вероятностей исправной работы:
P(1)(t) = 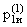 (t) +
(t) + 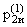 (t) = 1,076×e-3,459t - 0,076×e-9,541t,
(t) = 1,076×e-3,459t - 0,076×e-9,541t,
где верхний индекс (1) показывает, что они вычислены для определенного начального режима R1.
Аналогично, для начального режима R2:
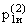 (t) = 0,493× (e-3,459t - e-9,541t),
(t) = 0,493× (e-3,459t - e-9,541t),
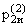 (t) = 0,089× e-3,459t + 0,911× e-9,541t,
(t) = 0,089× e-3,459t + 0,911× e-9,541t,
P(2)(t) = 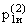 (t) +
(t) + 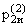 (t) = 0,582× e-3,459t + 0,418× e-9,541t.
(t) = 0,582× e-3,459t + 0,418× e-9,541t.
Если начальный режим работы системы в точности неизвестен, а известны только вероятности режимов R1 и R2 в начале процесса, надежность системы может быть подсчитана по формуле полной вероятности:
P(t) = P(R1) P(1)(t) + P(R2) P(2)(t),
где P(R1),P(R2)- вероятности того, что в начальный момент имеют место режимы R1 и R2 соответственно.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 5445; Нарушение авторских прав?; Мы поможем в написании вашей работы!