Преобразование Лапласа и его свойства

Лекция 1

Основы операционного исчисления

Допоміжна

Базова

1. Солодков А.С., Физиология человека. Общая. Спортивная. Возрастная: Уч. / А.С. Солодков., Е.Б. Сологуб – М.: Терра-Спорт, Олимпия-Пресс, 2001.– 520 с.

2. Дубровский В.И. Спортивная физиология: учебник для сред. и высш. учеб. заведений по физ. культуре. / В.И. Дубровский – М.: Гуманитар. изд. центр ВЛАДОС, 2005. – 462с.

3. Волков Н.И. Биохимия мышечной деятельности: Учебник. / Н.И Волков, Э.Н. Нессен., А.А. Осиненко, С.Н. Корсун − Киев.: Олимпийская литература, 2000.− 503 с.

4. Уилмор Дж.Х. Физиология спорта (перевод с английского): Учебник. / Дж.Х. Уилмор, Д.Л. Костилл – Киев: Олимпийская литература, 2001. − 503 с.

Операционное исчисление применяется при нахождении как частных, так и общих решений линейных дифференциальных уравнений любого порядка с постоянными коэффициентами, при этом правая часть уравнения на различных интервалах может быть задана различными аналитическими выражениями, а также может иметь точки разрыва. Операционный метод используется для решения однородных и неоднородных систем дифференциальных уравнений, причем правые части неоднородных систем также могут быть заданы на различных интервалах различными аналитическими выражениями и иметь точки разрыва.

Операционное исчисление широко применяется для решения задач электротехники и теории автоматического регулирования, в частности позволяет найти установившийся ток в колебательном контуре при периодическом и непериодическом внешнем напряжении. Операционные методы позволяют рассчитывать процессы в сложных электрических цепях при произвольном внешнем напряжении. Операционные методы позволяют также находить решения уравнений в частных производных, которые появляются в задачах математической физики, например при решении задачи о колебательном движении струн и стержней, о распространении тепла в стержне, плоских пластинах и пространственных телах, о распространении электрических колебаний вдоль длинных цепей.

Операционное исчисление строится на основе преобразования Лапласа.

Преобразованием Лапласа или изображением по Лапласу функции 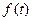вещественной переменной 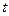называется функция 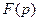комплексной переменной , определяемая несобственным интегралом

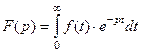. (1)

Интегралом Лапласа называется интеграл в правой части (1).

Оригиналом называется функция вещественной переменной 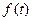, которая удовлетворяет условиям:

1) 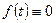при ,

2) 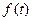кусочно-непрерывна при 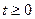; (2)

3) при любом 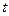, где 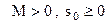некоторые постоянные числа. Число 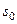называется п оказателем роста функции 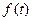или абсциссой сходимости интеграла Лапласа.

Функция 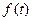может иметь на каждом отрезке при 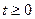лишь конечное число точек разрыва первого рода.

Иногда преобразованием Лапласа называется операция перехода от оригинала 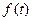к изображению 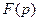. Соответствие между 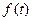и 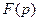записывается в виде .

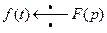Если функция 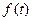является оригиналом, то интеграл Лапласа сходится абсолютно и равномерно на комплексной полуплоскости .

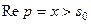Доказательство. Пусть , и 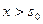. Тогда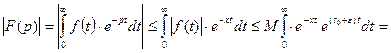

.

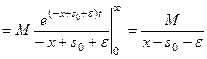Отсюда следует, что интеграл Лапласа сходится абсолютно при 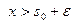, так как он мажорируется абсолютно сходящимся интегралом. Если же 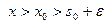, то , где в правой части неравенства получено число. Следовательно, интеграл Лапласа сходится равномерно при .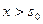

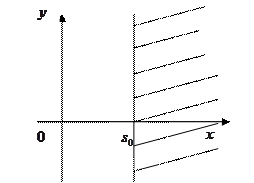
Преобразование Лапласа устанавливает связь между оригиналами 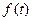и их изображениями. Определенным действиям, производимым над оригиналами соответствуют некоторые действия, производимые над их изображениями, причем действия над изображениями оказываются более простыми, чем над оригиналами. В частности, дифференциальному уравнению относительно оригинала соответствует алгебраическое уравнение относительно изображения. Если решить это алгебраическое уравнение и затем найти оригинал полученного решения, то тем самым будет получено решение исходного дифференциального уравнения.

Единичной функцией Хевисайда называется функция . График функции Хевисайда имеет вид

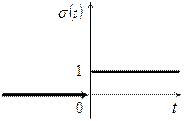
Пример 1. Найти изображение единичной функции Хевисайда.

,

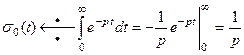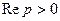
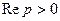(3)

Условимся в дальнейшем под функцией 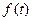понимать функцию, которая равна нулю при , т.е. .

Пример 2. Найти изображение показательной функции .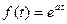

для .

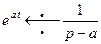
(4)

Пример 3. Найти изображение степенной функции , 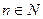и , .

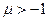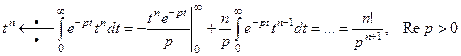
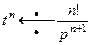
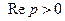(5)

Дата добавления: 2014-01-07