Соответствия, отображения, функции

Определение 2.1.1. Пусть X и Y – два непустых множества. Если определен способ сопоставления элементов Y элементам Х, то говорят, что между множествами Х и Y установлено соответствие. Если обозначить соответствие q, то запись q: X ® Y обозначает существование данного соответствия между множествами Х и Y. При этом совершенно не обязательно, чтобы в сопоставлении участвовали все элементы множеств Х и Y. Для того чтобы задать соответствие между множествами Х и Y, нужно задать множество Q Í X ´ Y = {(x, y) | x Î X, y Î Y }, определяющее закон, по которому осуществляется соответствие, то есть перечисляющий все пары (х, у), участвующие в сопоставлении.

Таким образом, соответствие, обозначаемое q, представляет собой тройку множеств:

q = (X, Y, Q),

в которой Q Í X ´ Y. В этом выражении первую компоненту X называют областью отправления соответствия, вторую компоненту Y – областью прибытия соответствия, третью компоненту Q – графиком соответствия. Термин «график» будет более подробно разъяснен при рассмотрении частного вида соответствия, называемого функцией.

Кроме рассмотренных множеств X, Y и Q с каждым соответствием q неразрывно связаны еще два множества: множество D (q) = { x Î X | (x, y) Î Q }, называемое областью определения соответствия, которое состоит из всех элементов множества Х, участвующих в сопоставлении, и множество E (q) = { y Î Y | (x, y) Î Q }, называемое областью значений соответствия, которое состоит из всех элементов множества Y, участвующих в сопоставлении. Если (х, у) Î Q, то говорят, что элемент y соответствует элементу х. Геометрически это удобно изображать стрелкой, направленной от х к у.

Множество всех у Î E (q), соответствующих фиксированному элементу х Î D (q), называется образом х в Y при соответствии q и обозначается q (x). Множество всех х Î D (q), которым соответствует фиксированный элемент у Î E (q), называется прообразом y в Х при соответствии q и обозначается q ^–1(y). Если С Í D (q), то образом множества С q (C) называется объединение образов всех элементов из С. Aналогично определяется прообраз множества D q ^–1(D) для любого D Í E (q) как объединение прообразов всех элементов из D.

Определение 2.1.2. Если D (q) = Х, то соответствие q называется всюду определенным или отображением Х в Y (в противном случае соответствие называется частичным). Если E (q) = Y, то соответствие q называется сюръективным (сюръекцией) на Y. Соответствие q называется инъективным (инъекцией), если любые различные х ₁ и х ₂ из D (q) имеют различные образы и любые различные у ₁ и у ₂ из E (q) имеют различные прообразы при соответствии q.

Два отображения р и q называются равными (обозначение p = q), если их область определения – одно и то же множество Х, и для любого х Î Х р (х) = q (х).

Отображение, для которого область определения и область прибытия являются одним и тем же множеством Х, часто называют преобразованием множества Х.

Определение 2.1.3. Соответствие q называется функциональным (или однозначным), если образом любого элемента х Î D (q) является единственный элемент у Î E (q), что обычно записывается как или q (x) = y. Соответствие q между множествами Х и Y называется взаимно однозначным или биективным (биекцией, иногда 1-1-соответствием), если оно всюду определено, сюръективно и инъективно. Однозначное отображение называется функцией. Функция называется инъективной, если различным х ₁ и х ₂ из Х соответствуют различные у ₁ и у ₂ из Y, и сюръективной, если она сюръективна как соответствие. Функция называется биективной, если она одновременно инъективна и сюръективна.

Определение 2.1.4. Пусть f: X ® Y – функция. Каждому элементу х Î Х f ставит в соответствие единственный элемент у Î Y: f (х) = у. Элемент х называется аргументом функции, у – значением функции на х. Если Е (f) состоит из единственного элемента, то f называется функцией-константой. Тождественной функцией на множестве Х называется функция е_X: Х ® Х, такая что e_X (х) = х для любого х Î Х. Если X, Y Í R, то функцию f называют вещественной.

Определение 2.1.5. Если f – вещественная функция, то упорядоченные пары (х, f (х)) можно изобразить в виде точек на плоскости R ². Полная совокупность таких точек будет представлять собой график функции f.

Например, график функции f: [–1; 1] ® [0; 1] Q_f = {(x, y) Î R ² | x ² + y ² = 1} = = Г представлен на рис. 2.1.1.

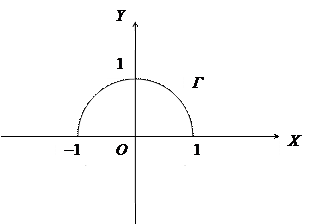Рис. 2.1.1

Определение 2.1.6. Для каждого соответствия q = (Х, Y, Q) с Q Í X ´ Y существует обратное соответствие, которое получается, если данное соответствие q рассматривать в обратном направлении, то есть определять элементы х Î Х, с которыми сопоставляются элементы у Î Y. Соответствие, обратное соответствию q, будем обозначать

q ^–1 = (Y, X, Q ^–1),

где Q ^–1 Í Y ´ X. Геометрическое представление обратного соответствия получается путем изменения направления стрелок в геометрическом представлении прямого соответствия. Отсюда следует, что обратным соответствием для обратного соответствия будет прямое соответствие:

(q ^–1)^–1 = q.

Пример 2.1.1. Пусть Х = {1, 2}, Y = {3, 5}, так что Х ´ Y = {(1, 3), (1, 5), (2, 3), (2, 5)}. Это множество дает возможность получить 2⁴ = 16 различных соответствий. Графики соответствий: Q ₀ = {()} = Æ, Q ₁ = {(1, 3)}, Q ₂ = {(1, 5)}, Q ₃ = {(2, 3)}, Q ₄ = {(2, 5)}, Q ₅ = {(1, 3), (1, 5)}, Q ₆ = {(1, 3), (2, 3)}, Q ₇ = {(1, 3), (2, 5)}, Q ₈ = {(1, 5), (2, 3)}, Q ₉ = {(1, 5), (2, 5)}, Q ₁₀ = {(2, 3), (2, 5)}, Q ₁₁ = {(1, 3), (1, 5), (2, 3)}, Q ₁₂ = {(1, 3), (1, 5), (2, 5)}, Q ₁₃ = {(1, 3), (2, 3), (2, 5)}, Q ₁₄ = {(1, 5), (2, 3), (2, 5)}, Q ₁₅ = {(1, 3), (1, 5), (2, 3), (2, 5)} = X ´ Y. Обозначим q_i соответствие с графиком Q_i, .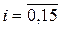

Областью определения соответствия q ₉ является {1, 2} = X, поэтому q ₉ – отображение. Областью значений q ₉ является {5} ¹ Y, поэтому q ₉ не сюръективно. 5 является образом 1 и 2 при соответствии q ₉, поэтому q ₉ не инъективно. Образом множества Х при соответствии q ₉ является множество {5}. Прообразом множества {5} при соответствии q ₉ является множество Х. Соответствие q ₉ функционально, так как каждый из элементов 1 и 2 имеет единственный образ – элемент 5.

На рис. 2.1.2а изображено геометрическое представление соответствия q ₁₁. Графиком обратного соответствия q ₁₁^–1 является множество Q ₁₁^–1 = {(3, 1), (5, 1), (3, 2)}. Геометрическое представление q ₁₁^–1 приведено на рис. 2.1.2б.

Рис. 2.1.2

Отображениями являются соответствия q ₆– q ₉, q ₁₁– q ₁₅. Сюръективными соответствиями являются q ₅, q ₇, q ₈, q ₁₀– q ₁₅. Функциональными соответствиями являются q ₁– q ₄, q ₆– q ₉. Инъективные соответствия: q ₁– q ₄, q ₇, q ₈. Функциями являются q ₆– q ₉. Биективные функции: q ₇, q ₈. ·

В дальнейшем будем рассматривать только функциональные соответствия, которые также иногда для краткости будем называть функциями.

Перечислим основные способы задания функций.

1. Наиболее простой способ задания функций – это табличный. Таблицы при этом представляют собой конечные списки пар (х, f (х)). Однако таким способом могут быть заданы только функции, определенные на конечных множествах.

2. Другим не менее известным способом задания функций является аналитический или формула, описывающая функцию с помощью суперпозиции других (исходных) функций. Если способ вычисления исходных функций известен, то формула задает процедуру вычисления данной функции как некоторую последовательность вычислений исходных функций.

Иногда для разных подмножеств множества Х при задании функции приходится пользоваться различными формулами. Пусть А_i Ì Х, , X = A ₁ È…È A_n, А_i Ç А_j = Æ при i ¹ j. Обозначим через f_i (х) формулу, определяющую у при х Î А_i, 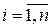. Тогда функция f, определенная на всем множестве Х, задается так:

Так, функцию f (х) = | х | можно задать в виде:

3. Если f – вещественная функция, то она может быть задана графически на плоскости R ², как это уже говорилось в определении 2.1.5.

4. Вычисления функций по таблицам, формулам, а также с помощью графиков являются частными видами вычислительных процедур. Существуют вычислительные процедуры, не относящиеся к указанным трем видам. Среди них особенно следует выделить рекурсивные процедуры. Рекурсивная процедура задает функцию f, определенную на множестве N (Z _³0), следующим образом: 1) задается значение f (1) (f (0)); 2) значение f (n + 1) определяется через суперпозицию f (n) и других, считающихся известными, функций. Простейшим примером рекурсивной процедуры является вычисление функции n!: 1) 0! = 1; 2) (n + 1)! = n!(n + 1). Для вычисления (n + 1)! при n Î N требуется n – 1 умножений, то есть число вычислительных шагов увеличивается с ростом аргумента.

Пример 2.1.2. Пусть X = Y = R, f: X ® Y, где .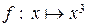

f является числовой функцией, поскольку D (f) = R и данное отображение однозначно.

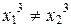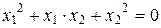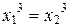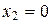Пусть , тогда , так как иначе получаем . Поскольку , получаем, что . Но при дискриминант и равенство невозможно ни для каких . Если , то 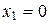и получается противоречие тому, что . Итак, f – инъективная функция.

Для при 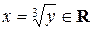. Поэтому f – сюръективная функция.

Значит, данная функция f: X ® Y биективна. ·

Определение 2.1.7. Пусть даны две функции f: X ® Y ₁ и g: Y ₂ ® Z, Y ₁ Í Y ₂. Функция h: X ® Z называется композицией функций f и g, обозначение h = g 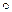f или h = gf, если h – последовательное применение функций f и g: для любого x Î X h (x) = g (f (x)). Часто говорят, что функция h получена подстановкой f в g.

Аналогично по индукции определяется композиция n отображений для любого натурального числа .

Пример 2.1.3. f: R ® R, g: R ® R, где f (x) = sin x, .

D (f) = R. Поскольку дискриминант D = 25 – 36 = –11 < 0, то x ² – 5 x + 9 > 0 " x Î R и функция g всюду на R определена. D (g) = R также. Построим композиции функций gf и fg. Очевидно, что D (gf) = D (fg) = R.

, при x = 0 gf (0) = 3;

, при x = 0 gf (0) = sin 3 ¹ 3 (| sin x | £ 1).

Итак, gf ¹ fg. ·

Лемма 2.1.1. Пусть даны функции f: Х ® Y и g: Y ® Х, причем их композиция gf = е_Х. Тогда f – инъекция, а g – сюръекция.

Пусть f не является инъекцией. Тогда найдутся два элемента х ₁, х ₂ Î Х, такие что х ₁ ¹ х ₂, но f (х ₁) = f (х ₂) = у Î Y. Тогда gf (х ₁) = gf (х ₂) = g (у), но так как gf = е_Х, то gf (х ₁) = х ₁, а gf (х ₂) = х ₂, и мы получили противоречие тому, что х ₁ ¹ х ₂. Итак, f – инъекция.

Теперь докажем, что g – сюръекция. Действительно, для любого х Î Х х = gf (х) = g (у) для некоторого у Î Y.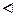

Для обратной функции удобно использовать еще одно определение.

Определение 2.1.8. Пусть функция f: Х ® Y. Функция f ^–1: Y ® Х называется обратной к функции f, если f ^–1 f = е_Х, а ff ^–1 = е_Y, где е_Х и е_Y – тождественные функции на множествах Х и Y соответственно.

Например, для кодирующей функции обратной будет декодирующая функция, которая каждому коду ставит в соответствие закодированный этим кодом объект. Если кодирующая функция не сюръективна, то декодирующая функция не всюду определена.

При аналитическом задании функции f принято аргумент как прямой, так и обратной функции обозначать одной и той же буквой, например, х. Поэтому для нахождения обратной функции следует уравнение у = f (х) разрешить (если это возможно) относительно х и поменять обозначения, заменив х на у и у на х. При этом формула для обратной функции запишется в виде: у = f ^–1(х).

Теорема 2.1.1 (критерий существования обратной функции). Функция f: X ® Y имеет обратную тогда и только тогда, когда f – биекция.

Необходимость. Пусть функция f имеет обратную f ^{– 1}: Y ® X. Тогда по определению обратной функции ff ^–1 = е_Y. Следовательно, по лемме 2.1.1 f – сюръекция. Также по определению обратной функции f ^{– 1} f = е_X. Тогда по лемме 2.1.1 f – инъекция. Одновременно будучи сюръекцией и инъекцией, f – биекция.

Достаточность. Пусть функция f биективна. Поскольку f сюръективна, для любого y Î Y существует х Î Х такой, что f (х) = у. Положим f ^{– 1}(у) = х. Значит, существует отображение f ^{– 1}: Y ® Х. Так как f инъективна, любой элемент у Î Y имеет единственный прообраз х Î Х. Поэтому, f ^–1 – функция. Очевидно, что f ^–1 является обратной к f функцией.

Свяжем с функцией еще одно понятие.

Определение 2.1.9. Пусть f: Х ® Y – произвольная функция, А Ì Х – произвольное непустое собственное подмножество Х. Сужением функции f на множество А называют функцию f_A, график которой состоит из тех и только тех пар (х, у), в которых х Î А, а значит, (х, y) Î А ´ Y.

Операцию сужения функции часто используют для табличного задания функций с бесконечной областью определения Х. В качестве множества А рассматривают обычно выборку равноотстоящих значений х множества Х. Получаемое при этом сужение f_A функции f уже легко представить в виде таблицы. По этому принципу построены таблицы логарифмов, тригонометрических функций и некоторые другие.

Может так случиться, что сама функция, заданная на множестве Х, не имеет обратной, но сужение этой функции на некоторое подмножество множества Х, на котором она инъективна, уже имеет обратную функцию, определенную на области значений исходной функции. Например, f (х) = х ², f: R ® R _³0, обратной функции на R _³0 не имеет, так как обратное отображение каждому у Î R _>0 ставит в соответствие два значения: и , где – арифметический квадратный корень. Такое отображение не функционально. Но отображения 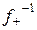: R _³0 ® R _³0, где 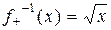и : R _³0 ® R _£0, где 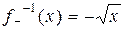, являются функциями, обратными соответственно к сужениям функции f на множества R _³0 и R _£0.

Пример 2.1.4. Рассмотрим примеры преобразований множеств X с различными свойствами.

1. X = R, f: X ® X, 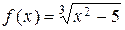. Функциональное отображение не инъективно, так как, например, , и не сюръективно, так как нет, например, такого x Î R, чтобы .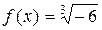

2. X = N, f: X ® X, . Функциональное отображение не сюръективно, так как, например, 1, 2, 3, 4 не имеют прообразов в N, и инъективно, поскольку при , так как иначе получим 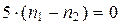, чего быть не может.

3. X = Z /6 Z, f: X ® X, 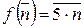. (5, 6) = 1, тогда по лемме 1.7.1 f – биекция:

4. X = Z /6 Z, f: X ® X, . (3, 6) = 3 > 1, тогда по лемме 1.7.2 f – не инъекция и не сюръекция:

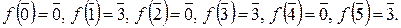
5. X = C, f: X ® X, . Функция f сюръективна, так как для 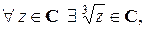такой что 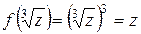. Но отображение не инъективно, потому что при 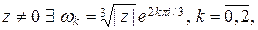– три различных значения аргумента со свойством .

6. X = R, f: X ® X, . f – биекция, как это было показано в примере 2.1.2. Сюръективность можно доказать и так: f – непрерывная на R функция, и . Отображение инъективно, потому что f – монотонно возрастающая функция на Х: производная при x ¹ 0, причем f (0) = 0, f (x) ¹ 0 при x ¹ 0.

7. X = Z, f: X ® X, . Функция инъективна, потому что она инъективна на R, как было показано в пункте 6 данного примера, а 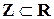. Но отображение не является сюръективным на Z, поскольку, например, 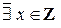такого, что . ·

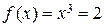Дата добавления: 2014-01-07