
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи, приводящие к понятию производной
|
|
|
|
Понятие производной функции в данной точке связано с понятиями касательной к графику функции в этой точке, мгновенной скорости и мгновенного ускорения движения материальной точки, мгновенной силой электрического тока, линейной плотностью стержня.
1.1. Геометрический смысл производной. Приведем определение касательной к графику функции в данной точке.
Пусть функция 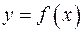 определена в некоторой окрестности
определена в некоторой окрестности 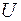 точки
точки 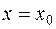 и непрерывна в этой точке. Через
и непрерывна в этой точке. Через 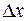 обозначим приращение аргумента. Будем предполагать, что точка
обозначим приращение аргумента. Будем предполагать, что точка 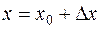 принадлежит данной окрестности
принадлежит данной окрестности 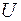 . Приращение функции, соответствующее приращению аргумента
. Приращение функции, соответствующее приращению аргумента 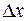 , обозначим
, обозначим 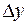 :
:
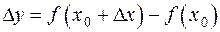 .
.
Рассмотрим секущую  (рис. 1), где
(рис. 1), где
 ,
,  ,
, 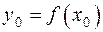 .
.

Рис. 1
Она записывается уравнением
 ,
,
где  – угловой коэффициент – определяется равенством
– угловой коэффициент – определяется равенством
 .
.
Из непрерывности функции 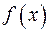 следует, что при
следует, что при 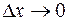 следует соотношение
следует соотношение 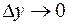 . Это означает, что точка
. Это означает, что точка  стремится вдоль графика функции к точке
стремится вдоль графика функции к точке 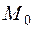 , так как
, так как
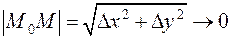 при
при 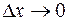 .
.
Если существует предельное положение секущей  при
при 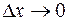 (то есть прямая
(то есть прямая  ), то его назовем касательной к графику функции
), то его назовем касательной к графику функции 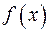 в точке
в точке 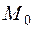 . Существование предельного положения секущей
. Существование предельного положения секущей  при
при 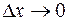 эквивалентно существованию предела
эквивалентно существованию предела
 . (1)
. (1)
Таким образом, если существует предел (1), то прямая, проходящая через точку 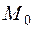 с угловым коэффициентом
с угловым коэффициентом  , является касательной к графику функции
, является касательной к графику функции 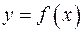 в точке
в точке 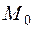 .
.
1.2. Скорость материальной точки. Пусть материальная точка движется по прямой и  – ее закон движения (
– ее закон движения ( – путь, пройденный точкой за время
– путь, пройденный точкой за время 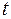 от начала движения. За промежуток времени от
от начала движения. За промежуток времени от 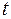 до
до  точка пройдет путь длины
точка пройдет путь длины 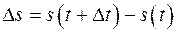 . Поэтому средняя скорость
. Поэтому средняя скорость 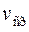 за этот промежуток времени равна
за этот промежуток времени равна
 .
.
Если рассматриваемое движение не является равномерным, то средняя скорость 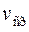 при фиксированном
при фиксированном 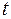 будет меняться при изменении
будет меняться при изменении 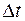 , и чем меньше
, и чем меньше 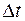 , тем лучше средняя скорость
, тем лучше средняя скорость 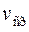 будет характеризовать движение точки в момент времени
будет характеризовать движение точки в момент времени 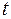 .
.
|
|
|
Скоростью материальной точки в момент времени 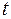 (мгновенной скоростью) называется предел средней скорости
(мгновенной скоростью) называется предел средней скорости 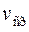 , когда
, когда 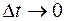 . Таким образом, мгновенная скорость материальной точки в момент времени
. Таким образом, мгновенная скорость материальной точки в момент времени 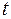 определяется равенством
определяется равенством
 .
.
1.3. Сила тока в данный момент времени. Пусть 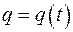 – количество электричества,
– количество электричества, 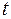 – данное время,
– данное время, 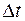 – некоторый промежуток времени, протекающее через поперечное сечение проводника,
– некоторый промежуток времени, протекающее через поперечное сечение проводника, 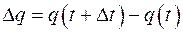 – количество электричества, протекающее через указанное сечение за промежуток времени от момента
– количество электричества, протекающее через указанное сечение за промежуток времени от момента 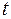 до момента
до момента  . Средней силой тока
. Средней силой тока 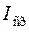 за промежуток времени
за промежуток времени 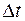 называется отношение количества электричества, протекающее через указанное сечение за промежуток времени
называется отношение количества электричества, протекающее через указанное сечение за промежуток времени 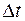 к данному промежутку времени:
к данному промежутку времени:
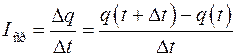 .
.
Силой тока в данный момент времени 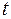 (мгновенной силой тока) называется предел средней силой тока
(мгновенной силой тока) называется предел средней силой тока 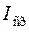 , когда
, когда 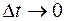 . Таким образом, мгновенная сила тока в момент времени
. Таким образом, мгновенная сила тока в момент времени 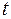 определяется равенством
определяется равенством
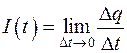 .
.
1.4. Линейная плотность неоднородного стержня. Стержень называется однородным, если два любых его участка одинаковой длины имеют одинаковую массу, и неоднородным, если участки одинаковой длины имеют разные массы.
Пусть дан неоднородный стержень длины  . Через
. Через  обозначим массу участка стержня длины
обозначим массу участка стержня длины 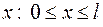 , отмеряемой от одного фиксированного конца (рис. 2). Масса части стержня, ограниченной точками, расположенными соответственно на расстоянии
, отмеряемой от одного фиксированного конца (рис. 2). Масса части стержня, ограниченной точками, расположенными соответственно на расстоянии 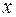 и
и
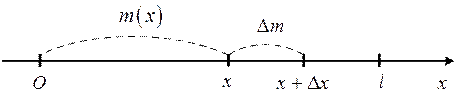
Рис. 2
 от указанного конца обозначим
от указанного конца обозначим
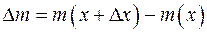 .
.
Отношение массы части стержня  к длине части
к длине части 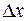 назовем средней линейной плотностью на указанном участке и обозначим
назовем средней линейной плотностью на указанном участке и обозначим 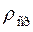 :
:
 .
.
Предел средней линейной плотности 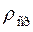 , когда длина участка
, когда длина участка 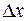 стремиться к нулю, назовем линейной плотностью стержня в данной точке и обозначается
стремиться к нулю, назовем линейной плотностью стержня в данной точке и обозначается  :
:
 .
.
Рассмотренные задачи, в которых речь идет о пределе отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, привели к появлению понятия производной функции – одного из важнейших понятий математики.
|
|
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1660; Нарушение авторских прав?; Мы поможем в написании вашей работы!