Виды систем линейных уравнений

ЛЕКЦИЯ 3

Тема 2: Системы линейных уравнений

Тема 3: Векторы

ПЛАН

1. Виды систем линейных уравнений.

2. Решение системы n линейных уравнений с n переменными:а)по формулам Крамера; б) с помощью обратной матрицы; в) методом Гаусса.

3. Теорема Кронекера-Капелли. Условие определенности и неопределенности совместной системы линейных уравнений.

4. Векторы. Операции над векторами. Понятие о векторном пространстве и его базисе.

5. Собственные векторы и собственные значения матрицы. Характеристическое уравнение матрицы.

Определение 1. Системой n линейных уравнений с n переменными называется система вида:

,

где a_ij (i =1,2,..., n; j =1,2,..., n) - коэффициенты при переменных;

b_i (i =1,2,..., n) - свободные члены.

Запишем систему линейных уравнений в матричной форме.

Обозначим ; ; .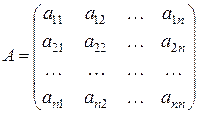

Имеем - матрица-столбец. Следовательно, по определению равенства матриц, систему уравнений можно записать в виде AX = B, где А - матрица коэффициентов при переменных, Х - матрица столбец переменных, В - матрица-столбец свободных членов.

Определение 2. Решением системы уравнений называется такой упорядоченный набор (k ₁, k ₂,..., k _n) чисел, при подстановке которых вместо переменных x ₁, x ₂,..., x _n каждое уравнение системы обращается в верное числовое равенство.

Определение 3. Система уравнений называется совместной, если она имеет хотя бы одно решение.

Определение 4. Система уравнений называется несовместной, если она не имеет решений.

Определение 5. Совместная система уравнений называется определенной, если она имеет единственное решение.

Определение 6. Совместная система уравнений называется неопределенной, если она имеет более одного решения.

Определение 7. Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений.

2. Решение системы n линейных уравнений с n переменными:

а) по формулам Крамера

Пусть дана система двух линейных уравнений с двумя переменными:

.

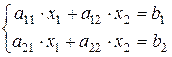Умножим первое уравнение на a ₂₂, второе уравнение на (- a ₁₂) и сложим их. Получим уравнение (a ₁₁ a ₂₂- a ₂₁ a ₁₂)× x ₁= b ₁ a ₂₂- b ₂ a ₁₂.

Умножим первое уравнение на (- a ₂₁), второе уравнение на a ₁₁ и сложим их. Получим уравнение (a ₁₁ a ₂₂- a ₂₁ a ₁₂)× x ₂= a ₁₁ b ₂- a ₂₁ b ₁.

Заметим, что ,

,

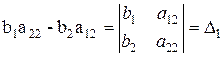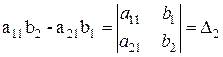
т.е. система имеет вид .

Если D¹0, то система имеет единственное решение , .

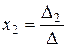Если D=0, а D₁¹0 или D₂¹0 то система несовместная.

Если D=0, D₁=0 и D₂=0, то система неопределенная и имеет бесконечное множество решений.

Теорема Крамера. Пусть D - определитель матрицы А системы n линейных уравнений с n переменными, D_j - определитель матрицы, полученной из матрицы А заменой j -го столбца столбцом свободных членов (j =1,2,..., n). Тогда, если D¹0, то система имеет единственное решение, определяемое по формулам

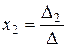, ,..., (формулы Крамера).

б) с помощью обратной матрицы (вывод формулы X = A ^-1 B)

В матричной форме система n линейных уравнений с n переменными записывается в виде А × Х = В, где , , .

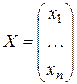Если ½ А ½¹0, то существует обратная матрица А ^-1. Умножая слева обе части матричного равенства А × Х = В на матрицу А ^-1, получим А ^-1(А × Х)= А ^-1 В. Но А ^-1×(А × Х)= (А ^-1× А)× Х = Е × Х = Х.

Следовательно, решением системы n линейных уравнений с n переменными методом обратной матрицы является матрица - столбец А ^-1 В.

в) методом Гаусса

Метод Гаусса - метод последовательного исключения переменных - заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последней переменной, находятся все остальные переменные.

Пусть дана система n линейных уравнений с n переменными:

(1).

Шаг 1. Предположим, что a ₁₁¹0. Умножаем первое уравнение на 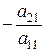, прибавляем его ко второму уравнению. Аналогично исключаем переменную x ₁ из остальных уравнений:

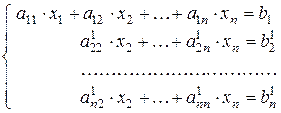(2).

Шаг 2. Предположим, что a ₂₂¹0. Исключаем переменную x ₂ из всех уравнений, начиная с третьего.

После (n -1)-го шага получаем систему треугольного вида

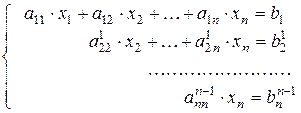(n).

Переход от системы (1) к равносильной системе (n) называется прямым ходом метода Гаусса.

Если , то .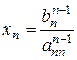

Далее, если 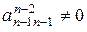, то .

Продолжая, находим все остальные переменные. Нахождение переменных из системы (n) называется обратным ходом метода Гаусса.

Замечание. Преобразования Гаусса удобно проводить не с самими уравнениями, а с матрицей их коэффициентов

,

называемой расширенной матрицей системы (1)

Дата добавления: 2014-01-07