Кольца полиномов над полями

Рассмотрим P [ x ] – множество полиномов (многочленов) от одной переменной x с коэффициентами из поля P. (P [ x ], +, ×) является кольцом с обычными операциями сложения и умножения полиномов. Это коммутативное и ассоциативное кольцо с единицей (1 Î P) и без делителей нуля, что следует из свойств умножения, правила вычисления старшего коэффициента в P [ x ] и свойств поля P. Условимся степень многочлена f (x) обозначать deg f (от англ. degree – «степень»). Степень нулевого многочлена часто считают неопределенной, но иногда будем считать ее нулевой, как степень многочлена, являющегося элементом поля P (0 Î P). По своим свойствам кольцо P [ x ] близко к кольцу целых чисел. Например, как и для Z, для кольца полиномов над полем имеют место следующие три теоремы.

Теорема 4.3.1. Обратимыми многочленами в кольце полиномов P [ x ] являются многочлены нулевой степени, отличные от нуля, и только они, то есть P [ x ]^* = P ^*.

Очевидно, что P ^* Í P [ x ]^*. Если f (x) Î P [ x ]^* и deg f ³ 1, то при умножении на f (x) любого многочлена, отличного от нуля, согласно правилу вычисления старшего коэффициента получим многочлен степени не ниже первой и, таким образом, не сможем получить 1 Î P – многочлен нулевой степени. Следовательно, deg f = 0, значит, f (x) Î P ^*. Поэтому P [ x ]^* Í P ^*. Итак, P [ x ]^* = P ^*.

Теорема 4.3.2 (о делении с остатком). Для любых двух многочленов f (x) и g (x) ¹ 0 из P [ x ] существуют единственные многочлены q (x) и r (x) из P [ x ] такие, что r (x) = 0 либо 0 £ deg r < deg g и выполняется равенство:

f (x) = g (x) × q (x) + r (x). (4.3.1)

Докажем существование пары многочленов q (x) и r (x), рассмотрев следующие случаи.

1. Если f (x) = 0, то, очевидно, q (x) = 0, r (x) = 0.

2. Если deg f < deg g, то f (x) = 0 × g (x) + f (x). Тогда q (x) = 0, r (x) = f (x).

3. Если deg f ³ deg g, то используется известный метод деления «уголком» f (x) на g (x), аналогичный методу деления целых чисел, для нахождения q (x) и r (x).

Теперь докажем единственность пары многочленов q (x) и r (x). Пусть f (x) = = g (x) × q ₁(x) + r ₁(x) = g (x) × q ₂(x) + r ₂(x), тогда g (x) × (q ₁(x) – q ₂ (x)) = r ₂(x) – r ₁(x), Þ r ₁(x) = r ₂(x), так как при r ₁(x) ¹ r ₂(x) получаем противоречие с тем, что 0 £ deg (r ₂ – r ₁) < deg g. Отсюда следует, что q ₁(x) = q ₂(x), поскольку g (x) ¹ 0.

Теорема 4.3.3. (P [ x ], +, ×) – кольцо главных идеалов.

В (P [ x ], +, ×), как в коммутативном кольце, все идеалы являются двусторонними.

1. Если идеал J = {0} в P [ x ], то J = < 0 > – главный идеал.

2. Если идеал J ¹ {0}, то в J найдем многочлен наименьшей степени, пусть это будет d (x). Покажем, что J = < d (x) >.

Очевидно, что < d (x) > Í J по определению идеалов J и < d (x) >.

Пусть f (x) Î J, тогда согласно теореме 4.3.2 существует единственная пара многочленов q (x) и r (x) таких, что выполняется равенство f (x) = q (x) d (x) + r (x), причем r (x) = 0 либо 0 £ deg r < deg d. Значит, r (x) = f (x) – q (x) d (x) Î J. Если r (x) ¹ 0, то deg r < deg d, а это противоречит тому, что d (x) – многочлен минимальной степени в J. Поэтому r (x) = 0 и f (x) Î < d (x) >, значит, J Í < d (x) >.

Итак, J = < d (x) >.

Определение 4.3.1. В равенстве (4.3.1) q (x) называют частным (неполным частным, если r (x) ¹ 0), а r (x) – остатком от деления f (x) на g (x). Если r (x) = 0, то говорят, что g (x), q (x) ¹ 0 – делители или множители полинома f (x). Также в этом случае говорят, что g (x) и q (x) ¹ 0 делят f (x), обозначение: g (x) | f (x), или f (x) кратно (делится на) g (x) и q (x) ¹ 0, обозначение: f (x) 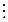g (x).

Если g (x) | f (x) и 0 < deg g < deg f, то многочлен g (x) называют нетривиальным делителем многочлена f (x). Очевидно, произвольный элемент a Î P ^* является делителем любого многочлена f (x) из P [ x ]. При f (x) ¹ 0 a ^–1 f (x) – также делитель f (x). Поэтому такие делители называют тривиальными.

Будем обозначать g (x)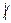 f (x), если g (x) ¹ 0 не делит f (x), и f (x) g (x), если f (x) не делится на g (x) ¹ 0.

Для многочленов из P [ x ] справедливы свойства делимости, аналогичные свойствам делимости в Z.

Дата добавления: 2014-01-07