Характеристика. Пусть в этом параграфе – ассоциативное и коммутативное кольцо с единицей e, без делителей нуля, где e ¹ 0

Пусть в этом параграфе 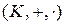– ассоциативное и коммутативное кольцо с единицей e, без делителей нуля, где e ¹ 0.

Функция f: Z ® K, где f (z) = z × e, " z Î Z, является, что легко проверить, кольцевым гомоморфизмом с Ker f = < n > при некотором n Î Z _³0. Согласно теореме 4.6.2 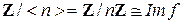, где Im f – некоторое подкольцо в K. Поскольку в 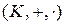нет делителей нуля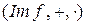, в и в 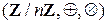также нет делителей нуля, поэтому либо 1) n = 0, либо 2) n = p – простое число. В первом случае K содержит в качестве подкольца кольцо, изоморфное Z и часто отождествляемое с Z. Во втором случае K содержит изоморфный образ 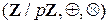в качестве подкольца, который также будем обозначать F_p.

Определение 4.7.1. Говорят, что кольцо 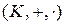в случае 1) имеет характеристику 0, а в случае 2) имеет характеристику p.

Таким образом, всякое поле имеет характеристику 0 или p, где p – простое число.

Можно дать и другое, эквивалентное определение характеристики и непосредственно показать, что в случае, когда она ненулевая, она является простым числом.

Определение 4.7.2. Если для кольца (K, +, ×) существует такое натуральное число n, что 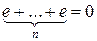, то наименьшее n с таким свойством называется характеристикой кольца K и обозначается char K (от англ. characteristic – «характеристика»).

Если для каждого n Î N 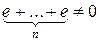, то говорят, что характеристика кольца равна 0.

Теорема 4.7.1. Если характеристика кольца отлична от 0, то она является простым числом.

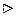Пусть характеристика кольца n является составным числом: 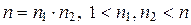. Тогда

,

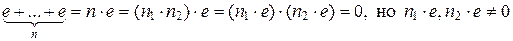Так как n – минимальное натуральное число со свойством 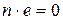, и получается противоречие тому, что в кольце нет делителей нуля. Поэтому n – простое число.

Пример 4.7.1. В поле F_p @ Z / p Z, где р – простое число, f – изоморфизм полей, char F_p = p. В самом деле, Z / p Z, а значит и F_p, являются аддитивными группами из р элементов и, следовательно по следствию 2 из теоремы Лагранжа 3.4.2, циклическими группами порядка р, порожденными в частности классом вычетов 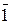и единицей поля F_p 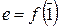соответственно. Следовательно, согласно структуре циклических групп имеем

Z / p Z = ,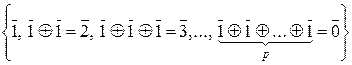

F_p .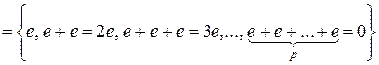

Это и означает, что char F_p = char Z / p Z = p. ·

Пример 4.7.2. Кольцо Z, а такжеполя Q, R и C имеют, очевидно, характеристику 0. ·

Пример 4.7.3. Пусть Р – поле характеристики р и y – вложение Р в кольцо 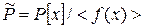для некоторого полинома f (x)Î P [ x ], 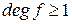, где y (a)=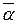, " a Î P. Тогда 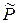– кольцо также характеристики р, поскольку 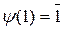и р – наименьшее натуральное число со свойством . ·

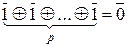Пример 4.7.4. Заметим, что существуют бесконечные по количеству элементов кольца и поля конечной характеристики. Примером такого кольца характеристики p для произвольного простого p является кольцо полиномов F_p [ x ], содержащее в качестве подкольца F_p. Поле рациональных функций или поле частных кольца F_p [ x ], то есть поле F_p (x) = { f (x)/ g (x) = 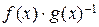| f (x), g (x)Î F_p [ x ], g (x) ¹ 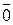} с естественными операциями сложения и умножения дробей, содержащее в качестве подполя F_p, имеет ту же характеристику p. ·

Пусть char K = р > 0. Тогда для любого n Î Z , где q Î Z, 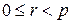, согласно теореме 1.1.1, и для каждого a Î K 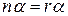, поскольку 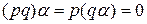. Отсюда следует своеобразная формула бинома Ньютона для частного случая степени в кольце K.

Лемма 4.7.1. В кольце 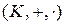с char K = р > 0

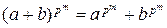(4.7.1)

для любых а, b Î K и для всякого натурального числа m.

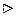Докажем справедливость формулы (4.7.1) методом математической индукции. При m = 1 все биномиальные коэффициенты при 1 £ k < p 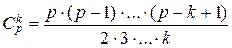являются натуральными числами и делятся на p в силу простоты р (ни один из сомножителей знаменателя не делится на p). Поэтому любых а, b Î K формула имеет вид:

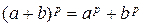. (4.7.2)

Предположим, формула (4.7.1) верна для 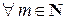. Докажем ее справедливость для m +1. Поскольку 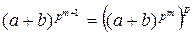, по предположению индукции и согласно формуле (4.7.2) при m = 1 получаем

.

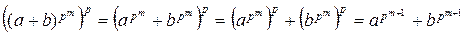Таким образом, формула (4.7.1) верна для любых а, b Î K и .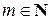

Определение 4.7.3. Минимальным или простым называется поле, не содержащее собственных подполей.

Теорема 4.7.2. Поле Q – минимальное поле характеристики 0, для любого простого р Z / p Z – минимальное поле характеристики р. Поля Q и Z / p Z не имеют других автоморфизмов кроме тождественного. В любом поле Р имеется в точности одно минимальное подполе, изоморфное либо Q, либо Z / p Z в зависимости от характеристики поля P.

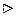Предположим, что P ₀ – подполе поля Q. Тогда 1Î P ₀, " m Î Z Þ m Î P ₀, " n Î Z \{0} Þ n ^–1Î P ₀, поэтому m × n ^–1Î P ₀. Таким образом, Q Í P ₀, следовательно, P ₀ = Q. Итак, Q – минимальное поле характеристики 0.

Пусть p – произвольное простое число. Предположим, что P ₀ – подполе поля Z / p Z. Тогда 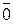Î P ₀, 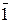Î P ₀, следовательно, 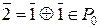,…, 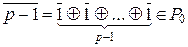. Таким образом, Z / p Z Í P ₀, следовательно, P ₀ = Z / p Z. Итак, Z / p Z – минимальное поле характеристики p.

Согласно определению автоморфизма поля и свойствам 3 и 4 гомоморфизмов колец получаем следующее. Если f: Q ® Q – автоморфизм, то f (1) = 1, f (m) = m × f (1) = m, " m Î Z, f (n ^–1) = f (n)^–1 = n ^–1, " n Î N, следовательно, для " m × n ^–1Î Q f (m × n ^–1) = f (m)× f (n ^–1) = m × n ^–1 и f – тождественный автоморфизм Q. Если f: Z / p Z ® Z / p Z – автоморфизм, то 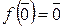, , 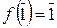тогда 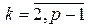, поэтому f – тождественный автоморфизм поля Z / p Z.

Пусть теперь P – произвольное поле. Как уже было показано в начале §4.7, если char P = 0, то P содержит в качестве подкольца изоморфный образ кольца Z, а если char P = p, то P содержит в качестве подполя изоморфный образ поля Z / p Z,обозначаемый F_p. Если char P = 0, то мономорфизм f: Z ® P можно продолжить до мономорфизма 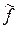: Q ® P, положив 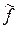(n ^–1) = f (n)^–1 для " n Î Z \{0}. Тогда Im 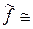Q – подполе поля P. Подполя F_p и Im 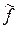также не имеют других автоморфизмов кроме тождественного.

Дата добавления: 2014-01-07