Основные понятия из теории вероятности

Математические основы надёжности АСОИУ

Событие – всякий факт, который в результате опыта может произойти или не произойти.

Случайное событие­­ – событие, которое может или не может произойти.

Достоверное событие – событие, которое должно произойти обязательно.

Невозможное событие – событие, которое не может произойти.

Если в результате опыта непременно должно появиться хотя бы одно из нескольких событий, то эти события образуют полную группу событий.

Суммой нескольких событий A ₁, A ₂, A ₃,…, A_n называется событие В, состоящее в появлении хотя бы одного из этих событий:

B = A ₁+ A ₂+ A ₃+ … + A_n. (2.1)

Произведением нескольких событий A ₁, A ₂, A ₃,…, A _n называется событие С, состоящее в совместном появлении всех событий:

C = A ₁Ÿ A ₂ Ÿ A ₃Ÿ … Ÿ A_n. (2.2)

Каждому случайному событию А поставлено в соответствие неотрицательное число Р (А), называемое его вероятностью.

Вероятность события представляет собой численную меру степени объективной возможности (частоты) появления этого события.

В качестве единицы измерения принимают вероятность достоверного события. Все другие события – возможные, но не достоверные – будут характеризоваться вероятностями, меньшими единицы, составляющими какую-либо долю единицы.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается как:

P _усл(A)= P (A / B) =P _B(A). (2.3)

Теорема сложения вероятностей: для произвольных событий А и В вероятность суммы этих событий выражается формулой:

P (A+B)= P (A)+ P (B)- P(A Ÿ B). (2.4)

Теорема умножения вероятностей: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

P (A Ÿ B)=P(A) Ÿ P(B/A)=P (B) Ÿ P(A/B). (2.5)

Из этой теоремы вытекают два следствия:

1) если событие А не зависит от события В, то событие В не зависит от события А;

2) вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Формула полной вероятности: если событие В может осуществляться с одним из n несовместимых событий A ₁, A ₂, A ₃,…, A_n, образующих полную группу и обычно называемых гипотезами, то полная вероятность события В определяется формулой:

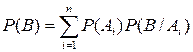. (2.6)

Формула Бернулли: если произошло последовательно n независимых опытов, в каждом из которых событие А может произойти с одной и той же вероятностью q, то вероятность того, что событие А произойдет ровно m раз, определяется по формуле Бернулли или по биноминальному распределению:

, (2.7)

где

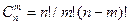. (2.8)

Случайной величиной Х называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.

Дискретная случайная величина – величина, принимающая только отделенные друг от друга значения, которые можно заранее перечислить.

Непрерывная случайная величина – величина, возможные значения которой непрерывно заполняют некоторый промежуток.

Если дискретная случайная величина Х принимает значения x ₁, x ₂, x ₃,…, x_m с заданными вероятностями P ₁, P ₂, P ₃,…, P_m, то соотношение устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения.

Непрерывная случайная величина имеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток. А так как сумма вероятностей отдельных значений случайной величины равна единице, то вероятность каждого значения должна стремиться к нулю. Поэтому вводится другая количественная характеристика - функция распределения, показывающая не вероятность события X=x_i, как закон распределения, а вероятность события Х<х, где х – некоторая текущая переменная:

F (x)= P (X < x). (2.9)

Функция F (x) существует как для прерывных, так и непрерывных случайных величин. Ее свойства: является неубывающей, т.е.

- F (x ₂)³= F (x ₁)³ при x ₂> x ₁, (2.10)

F (x)®0 при x ®-¥, (2.11)

F (x)®1 при x ®+¥, (2.12)

P (a<x<b)= F (b)- F (a). (2.13)

Плотность распределения:

f (x)= dF (x)/ d (x). (2.14)

Элемент вероятности dP – вероятность того, что случайная величина Х попадает на интервал dx около значения х:

dP = f (x) d (x). (2.15)

Наибольшее применение в практических задачах надежности находят показательные (экспоненциальные) и нормальные теоретические функции распределения для непрерывных случайных величин и закон Пуассона для дискретных случайных величин.

Показательное (экспоненциальное) распределение имеет следующий вид:

(2.16)

Нормальное распределение:

;

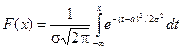(2.17)

.

Закон Пуассона позволяет определить вероятность того, что случайная величина, значениями которой могут быть только целые, неотрицательные числа, примет определенное значение:

. (2.18)

Математическое ожидание (среднее значение) случайной величины Х, принимающей дискретные значения x ₁, x ₂, x ₃ ,…, x_n, с вероятностями P ₁, P ₂, P ₃ ,…, P_n определяется как:

. (2.19)

Для непрерывной случайной величины математическое ожидание определяется как:

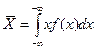. (2.20)

Так, имеем:

§ для экспоненциального распределения

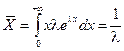; (2.21)

§ для нормального

; (2.22)

§ для закона Пуассона

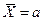. (2.23)

Основные свойства математического ожидания:

- математическое ожидание постоянной С равно этой же постоянной:

M [ C ] = C; (2.24)

- постоянный множитель выносится за знак математического ожидания:

M [ CX ] = CM [ X ]; (2.25)

- математическое ожидание суммы любых случайных величин (как угодно связанных) равно сумме их математических ожиданий:

M [ X+Y ] = M [ X ] + M [ Y ]; (2.26)

- математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

M [ XY ] = M [ X ] × M [ Y ]. (2.27)

Дисперсия определяется как математическое ожидание квадрата уклонения случайной величины от ее математического ожидания:

; (2.28)

дисперсия экспоненциального распределения:

D_x =1/l² ; (2.29)

§ дисперсия нормального распределения

D_x =s² ; (2.30)

§ дисперсия закона Пуассона

D_x = a. (2.31)

Дата добавления: 2014-01-07