Составление дифференциальных уравнений для вероятностей состояний

Главное преимущество пуассоновских систем в отношении их исследования состоит в том, что для этих систем вероятности состояний описываются с помощью обычных дифференциальных уравнений.

Рассмотрим методику вывода этих уравнений на примере исследования простой системы с двумя состояниями х ₀, х ₁ (рис. 2.13).

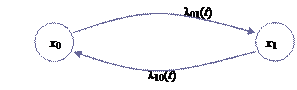
Рис. 2.13

Составим уравнение, определяющие вероятности р ₀(t) и р ₁(t) того, что система в любой момент времени t будет находиться в состоянии х ₀ и х ₁ соответственно. Рассмотрим момент времени t и дадим ему малое приращение D t. В этом случае р ₀(t+ D t) есть вероятность того, что в момент времени (t+ D t) система находится в состоянии х ₀. Это событие имеет два исхода.

А – система в t была в состоянии х ₀ и за время D t из него не вышла;

В – система в t была в состоянии х ₁ и за время D t перешла в состояние х ₀.

В силу ординарности пуассоновских потоков событий вероятность осуществления нескольких переходов ха малое время D t представляет собой величину высшего порядка малости по сравнению с D t ®(0(D t)).

Вероятность события А находится следующим образом. Это событие будет иметь место, если в момент времени t система будет находиться в состоянии х ₀ (вероятность этого р ₀(t) и за время D t не наступит ни одного события в потоке с интенсивностью l _0,1(t)).

Условная вероятность этого равна:

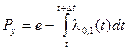. (2.71)

Следовательно,

. (2.72)

Считая величину D t малой, а l_0,1 – непрерывной функцией получим:

, (2.73)

где p ₀ (D t) –величина высшего порядка малости, чем D t.

Событие В будет иметь место, если система в момент времени t будет в состоянии х ₁ и в потоке событий с интенсивностью l_1,0(t) за время D t наступит хотя бы одно событие, а в потоке событий с интенсивностью l_0,1(t) за время D t не наступит ни одного события.

Считая l_1,0(t) непрерывной получим:

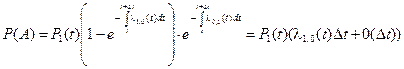. (2.74)

Применяя теорему сложения вероятностей, будем иметь:

, (2.75)

где D(D t) представляет собой сумму всех членов, порядок малости которых выше D t.

Проведя элементарные преобразования в выражении для p ₀(t+ D t), получим:

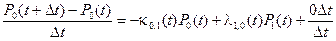, (2.76)

т.к. предел левой части представляет собой производную функцию р ₀(t), то окончательно дифференциальное уравнение для р ₀(t) примет вид:

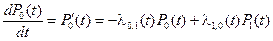. (2.77)

При выводе этого дифференциального уравнения использовались оба свойства пуассоновского потока событий:

- ординарность;

- отсутствие последействия.

Очевидно, пользуясь аналогичными рассуждениями и учитывая для каждого состояния все возможные переходы, связывающие это состояние с соседними, можно получить столько обыкновенных линейных дифференциальных уравнений, сколько имеется возможных состояний системы.

Для приведенного примера для P ₁(t):

. (2.78)

Естественно, для любого t должно соблюдаться условие:

p ₀(t)+ p ₁(t)=1. (2.79)

Таким образом, вероятности состояний р_i (t) для дискретной системы, в которой протекает марковский процесс с непрерывным временем, определяются системой обыкновенных линейных дифференциальных уравнений. Другими словами, если все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими, то вероятности состояний определяется обыкновенными линейными дифференциальными уравнениями. Если система в начальный момент времени находится заведомо в определенном состоянии x_m, то при t= 0 вероятность этого состояния p_m (0)=1, p_i (0) = 0 при i¹m.

В общем случае могут быть заданы вероятности всех состояний в начальный момент, отличные от 0 и 1, при соблюдении условия

. (2.80)

Используем следующий методический прием вывода дифференциальных уравнений для вероятностей состояний.

l₀₁(t)

Допустим, что система имеет четыре возможных состояния х ₀, х ₁, х ₂, х ₃ и может переходить из любого состояния в любое. Граф состояний такой системы следующий (рис. 2.4).

l₁₀(t)

l₂₃(t)

l₃₂(t)

l₃₀(t)

l₀₃(t)

l₂₁(t)

l₁₂ (t)

l₃₁(t)

l₁₃(t)

l₀₂(t)

l₂₀(t)

X₂

X₃

X₁

X₀

Рис. 2.4

У каждой стрелки, указывающей возможность и направление перехода, проставлены интенсивности пуассоновских потоков событий, переводящих систему из состояния в состояние по данной стрелке. Примем, что граф состояний, на котором представлены переходы и интенсивности соответствующих потоков событий, называть размеченным графом состояний.

При составлении дифференциальных уравнений для вероятности p_i (t), (i= 0 ..n) используем следующее мнемоническое правило.

Производная вероятности пребывания системы в состоянии x_i равна: 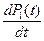, алгебраической сумме нескольких членов, число членов этой суммы равно числу стрелок на графе состояний системы, соединяющих состояние x_i с другими состояниями. Если стрелка направлена в состояние x_i, то член берется о знаком плюс, если стрелка направления из состояния x_i, то со знаком минус. Каждый член суммы равен произведению вероятности того состояния, из которого направлена стрелка, на интенсивность потока событий, переводящего систему по данной стрелке. Число отрицательных членов равно числу стрелок, направленных из состояния x_i, число положительных членов равно числу стрелок, направленных в это состояние.

Пользуясь этим правилом, составим дифференциальные уравнения для вероятностей состояний системы представленного графа системы:

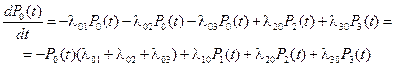(2.81)

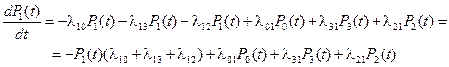(2.82)

и т.д.

При составлении этой системы дифференциальных уравнений можно короче записать ее таким образом:

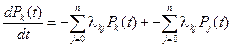. (2.83)

Полученный результат можно обобщить на случай, когда система имеет произвольное (n +1) число состояний (х ₀, х ₁, …, х_n).

Система уравнений для такой системы будет иметь вид

(2.84)

при к= 0, …, n.

Для того, чтобы проинтегрировать эту систему для уравнений, нужно задать начальные условия р ₀(0), р ₁(0), р ₂(0), …, р_n (0). На эти условия накладываются естественные ограничения

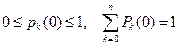. (2.85)

Если эти условия соблюдены, то для любого момента времени t решение системы уравнений должно соответствовать заданному условию, 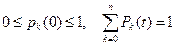так как в любой момент времени t система будет достоверно находится в каком-нибудь одном из своих состояний.

Полученную систему для уравнения можно составить только для пуассоновской системы, т.е. для системы, в которой переход осуществлялся под воздействием пуассоновского потока событий. При этом интенсивность в системе l _ij (t) могут быть любыми неотрицательными функциями времени.

Таким образом, допущение о марковском характере процесса, протекающего в системе с конечным числом состояний, приводит к необходимости анализа системы обыкновенных дифференциальных уравнений.

Если не делать предположения о том, что процесс, протекающий в системе, является марковским, то аналитическое исследование поведения системы требует привлечения более сложного математического аппарата. При этом в большинстве случаев получают решение, которое мало отличается от истинного. При этом погрешность решения, как правило, находится в пределах точности исходных данных. Так имитационные эксперименты показали, что в большинстве случаев эта погрешность ограниченна 3-5 %, в очень редких случаях доходит до 10-12 %. Это объясняется тем, что поток событий, протекающих в реальной системе, в силу предельных теорем теории потоков по своей структуре весьма близок к пуассоновскому.

Дата добавления: 2014-01-07