Построение графа состояний

Инженерная методика расчета показателей надежности типовых структур системы

Расчет показателей надежности проводится в следующей последовательности:

§ формулировка понятия отказа системы и представление исходных данных,

§ построение графа состояний,

§ составление системы дифференциальных уравнений,

§ определение вероятностей состояний системы,

§ вычисление и показателей надежности системы.

Отказ является понятием субъективным, поэтому его определение для конкретной системы согласуется с заказчиком. Исходными данными для расчета показателей надежности являются:

§ надежностно-функциональная схема (НФС) расчета надежности АСУТП,

§ интенсивности отказов и восстановлений каждого элемента системы,

§ количество ремонтных бригад,

§ приоритет обслуживания,

§ начальное состояние процесса функционирования системы,

§ время непрерывной работы системы.

Граф состояний строится в следующем порядке:

1) наметить в виде горизонтальных линий уровни графа и пронумеровать их сверху вниз, считая верхний уровень нулевым;

2) возможным состояниям системы поставить в соответствие узлы графа, располагаемые на определенных уровнях в виде точек (или кружков); на 0-м уровне помещаются узлы, соответствующие состояниям, когда все элементы системы исправны; на 1-м уровне помещаются узлы, соответствующие состояниям, когда отказал любой один элемент системы; на 2-м уровне помещаются узлы, соответствующие состояниям, когда отказали любые два элемента системы, и т.д.

3) при наличии непосредственного перехода из состояния в состояние соответствующие узлы соединяются линиями-ветвями графа, в ветви ставятся интенсивности отказов или интенсивности восстановлений элементов, из-за которых осуществляются переходы из состояния в состояние; направления переходов указываются стрелками; в случае резервированных систем с одинаковыми интенсивностями отказов и восстановлений элементов узлы графа могут объединяться, отказовые состояния графа помечаются, например, крестами.

Если вычисляются P (t) и T ₀, то в графе отсутствуют ветви переходов из всех отказовых состояний. Это отмечается пунктирной линией, называемой экраном, перечеркивающей соответствующую ветвь.

Составление системы дифференциальных уравнений. По виду графа формально записывается система линейных дифференциальных уравнений для вероятностей p_k (t) пребывания системы в момент времени t в состоянии k. В левую часть уравнения записывается производная по времени p’_k (t), в правую часть - сумма произведений интенсивностей переходов из всех соседних состояний в состояние k, умноженных на соответствующие вероятности, минус сумма произведений интенсивностей переходов из состояния k во все соседние состояния, умноженных на вероятность p_k (t) Для произвольного состояния k (k= 0, 1, 2, ..., n) уравнение имеет вид:

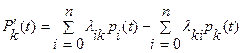(4.27)

,

где l _ik, l _ki интенсивности перехода из состояния i в состояние k и из состояния k в состояние i соответственно. Если в графе отсутствует переход из состояния i в состояние k, или из состояния k в состояние i, то считается, что соответствующая интенсивность перехода -l _ik, или l _ki равна нулю.

Проверяется правильность составления системы дифференциальных уравнений: если сумма правых частей равна нулю, то считается, что система составлена правильно.

Для определения вероятности безотказной работы следует ограничиться составлением уравнений только для исправных состояний системы.

Определение вероятностей состояний системы. Вероятности p_k (t) определяются путем решения системы любым из известных в математике методов. Наиболее целесообразно использовать метод преобразования Лапласа. Для этого в уравнениях вместо вероятностей p_i (t) необходимо поставить их изображения p_i (s), а вместо производных p ¢ _k (t) - выражения sp_k (s) -p_k (t) |t =0, тогда система дифференциальных уравнений в преобразованиях Лапласа записывается в виде следующей системы алгебраических уравнений:

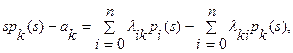(4.28)

где a_k=p_k (t) |t=0 - вероятность пребывания системы при t= 0 в состоянии k. Эти вероятности определяются начальными условиями функционирования системы. В большинстве случаев при t= 0 все элементы системы находятся в исправном состоянии, тогда a ₀=1, a _k=0, (k= 1,2,… ,n).

В результате решения системы алгебраических уравнений определяются p _k(s). Находятся оригиналы p_k (t) функций p_k (s) по любому известному методу.

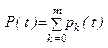Определение вероятности безотказной работы. Вероятность безотказной работы P (t) вычисляется по формуле:

(4.29)

Суммирование в формуле производится по всем m +1 исправным состояниям системы.

Определение средней наработки до отказа. Средняя наработка до отказа T ₁ вычисляется по формуле:

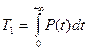. (4.30)

Формулой целесообразно пользоваться, в том случае, когда вероятность безотказной работы представлена в явном виде:

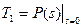. (4.31)

Формулой целесообразно пользоваться, если вероятность безотказной работы вычислялась с помощью преобразования Лапласа.

При неизвестной выражении для вероятности безотказной работы P (t) или P (s) средняя наработка до отказа вычисляется по формуле

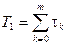, (4.32)

где t_k - среднее время пребывания системы в k -м исправном состоянии, определяемое из следующей системы алгебраических уравнений:

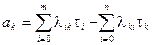. (4.33)

k= 0,1 ,…,m.

Система записывается по виду графа, в котором поставлены экраны из всех отказовых состояний. Формально система может быть получена из системы (4.28) при s= 0.

Определение функции готовности. Функция готовности K _г(t) вычисляется по одному из следующих соотношений

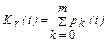(4.34)

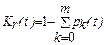или

(4.35)

где p_k (t) - вероятность пребывания системы в момент времени t в состоянии k.

Если число исправных состояний в графе меньше или равно числу отказовых состояний, то следует пользоваться соотношением (4.34), в противном случае целесообразно использовать соотношение (4.35).

Определение коэффициента готовности. Коэффициент готовности K _г вычисляется по одному из следующих выражений:

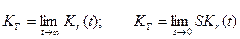. (4.36)

Приведенными формулами целесообразно пользоваться, если известны функция готовности или ее преобразование Лапласа.

Если функция готовности и ее изображение не известны, то K _г находится по формуле

,

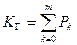где 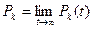- финальное значение вероятности пребывания системы в состоянии k. Вероятности p_k (k =0,1,…, n -1) вычисляются путем решения следующей системы линейных уравнений:

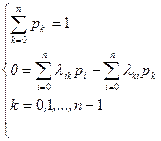
(4.37)

Эта система формально получается из системы, если левые части всех уравнений положить равными нулю.

Определение наработки на отказ. Наработка на отказ Т ₀ вычисляется по одному из следующих соотношений:

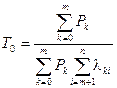(4.38)

или

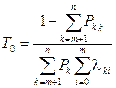, (4.39)

где 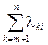- сумма интенсивностей переходов из состояния k во все отказовые состояния, а 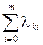- сумма интенсивностей переходов из состояния k во все исправные состояния.

Формулой (4.38) удобно пользоваться, если число исправных состояний меньше или равно числу отказовых состояний, в противном случае целесообразно пользоваться формулой (4.39).

Предотказовым является состояние, соответствующее узлу графа, из которого есть переход хотя бы в одно отказовое состояние.

Если граф имеет лишь одно предотказовое состояняе, то наработка на отказ может быть вычислена по формуле:

, (4.40)

где t _k определяются путем решения системы линейных уравнений при следующих начальных условиях: вероятность предотказового состояния равна единице, а все остальные вероятности равны нулю. Этот способ позволяет упростить вычисление наработки на отказ в связи с уменьшением размерности системы алгебраических уравнений.

Если известно среднее время восстановления системы` T _в и коэффициент готовности K _г, то наработка на отказ вычисляется по формуле:

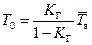. (4.41)

Формулой удобно пользоваться, если в графе имеется лишь одно отказовое состояние или интенсивности переходов из всех отказовых состояний одинаковы.

Определение среднего времени восстановления. Среднее время восстановления Т _в вычисляется по одному из следующих соотношений:

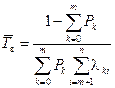(4.42)

или

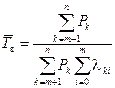. (4.43)

Если в графе имеется лишь одно отказовое состояние, то` Т _в вычисляется по формуле:

, (4.44)

где n - номер состояния отказа системы.

Если интенсивности переходов из всех отказовых состояний одинаковы и равны, то

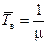, (4.45)

где m - интенсивность восстановления.

Дата добавления: 2014-01-07