Clauses

Сведение задач к подзадачам

Поиск в ширину

Поиск в глубину и итеративное углубление

Поиск с возвратами

Стратегии поиска в пространствах состояний

5.4. Эвристический поиск по заданному критерию: основные понятия; алгоритм А*.

5.5.1. Представление задач в виде графов AND/OR

5.5.2. Примеры представлений в виде графа AND/OR

5.1. Графы: основные понятия; задача поиска пути в графе, ее программирование на языке Турбо-Пролог.

Граф G определяется как пара G:= (V,E),где V – непустое множество, его элементы называются вершинами графа; E- некоторое множество упорядоченных пар вершин – дуг графа или система двухэлементных частей множества V – ребер графа; в первом случае граф называют ориентируемым (орграфом), во втором – неориентируемым (или просто графом). Графы представляются геометрическими фигурами: вершинам сопоставляются точки плоскости (узлы графа); дугам (в случае орграфа) сопоставляются направленные (стрелкой ко второму узлу пары) линии произвольной формы; ребрам сопоставляются ненаправленные линии, соединяющие соответствующие узлы. Графы являются универсальным средством для представле­ния бинарных отношений (соответственно, их визуализации) и широко используются в приложениях. Вершинам, ребрам (дугам) могут быть поставлены в соответствие различные метки для обозначения: имен, цен, пропускных способностей линий и т.д.,тогда граф называется размеченным. Примеры графов показаны на рис. 5.1.

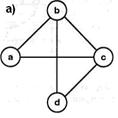
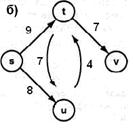
Рис.5.1. Примеры графов: а) простой граф; б) ориентированный размеченный граф.

Приведем варианты задания этих графов. на языке Турбо-Пролог. 1. а).Определим предикаты: v(X)- X - вершина графа, rn(X,Y)- {X, Y} – ребро неупорядоченного графа. Тогда первый граф можно представить как систему фактов:

v(a). v(b). v(c). v(d).

rn(a,b). rn(c,b). rn(c,a). rn(c,d). rn(b,d).

б). Определим предикаты: ov(X)- X – вершина орграфа, do(X,Y,Z)- (X,Y)- дуга орграфа с меткой Z. Второй граф представляется системой фактов:

ov(s). ov(t). ov(u). ov(v).

do(s,t,9). do(t,v,7). do(s,u,8).

do(t,u,7). do(u,t,4).

2. Граф может быть задан атомарной формулой согласно его определению, то есть как пара множеств: узлов и ребер(дуг).

а).

graph([a,b,c,d], [e(a,b), e(b,d), e(b,c), e(c,d)]).

б).

graphor([s,t,u,v], [a(s,t,9), a(t,v,7), a(t,u,7), a(u,t,4), a(s,u,8)]).

В этих представлениях t(X,Y), a(X,Y,Z) предикаты,задающие ребра первого и соответственно дуги второго графов.

Существуют и другие методы представления графов в системе Турбо- Пролог. Выбор наиболее подходящего представления зависит от приложения и от того, какие операции должны выполняться с графами.

Путь (path) на графе — это последовательность дуг, соединяющих соседние вершины. Путь представляется списком вершин, задающих дуги пути, систематизированным в порядке их следования.

Корневой граф содержит единственную вершину, от которой существует путь к любой вершине графа. Эта вершина называется корнем (root). При изображении корневого графа корень обычно помещают в верхней части рисунка над всеми остальными вершинами.

Дерево (tree) — это граф, на котором для любых двух вершин существует не более одного пути между ними. Деревья обычно имеют корни, которые изображаются в верхней части рисунка, как и для корневых графов. Поскольку для каждой вершины дерева существует не более одного пути в эту вершину из любой другой вершины, то не суще­ствует путей, содержащих петли (дуги с совпадающими вершинами) или циклы (замкнутые пути).

Для корневых деревьев или графов отношения между вершинами описываются понятиями родителя, потомка и вершин-братьев (siblings) — вершин дерева, имеющих общую вершину-родителя. Они используются в обычном смысле наследования: при проходе вдоль направленной дуги родитель предшествует потомку. Концы всех направленных дуг, исходящих из одной вершины, называются вершинами-братьями. Аналогично на пути ориентированного графа предок предшествует потомку. На рис. 5.2 вершина a является родителем вершин b, c и d (которые являются потомками a и вершинами-братьями). Вершины а и b являются предками вершин e, f, а вершины д, h, i являются потомками а.

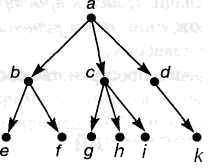
Рис. 5.2. Корневое дерево как схема семейных отношений.

Одной из самых распространенных задач на графах является.

поиск пути между двумя указанными узлами графа.

Предположим, что G — граф, а А и Z — два узла в графе G. Определим следующее отношение:

path(A, Z, G, Р)

где Р — ациклический путь между узлами А и Z в графе G. Путь Р представлен как список узлов в этом пути. Если G — граф, показанный на рис. 5.2., то имеют ме­сто следующие варианты пути:

path(a, d, G, [a,b,d]) path(a, d, G, [a,b,c,d])

Поскольку путь не должен содержать циклов, то любой узел может входить в со­став пути не больше одного раза. Ниже описан один из методов поиска пути.

Чтобы найти ациклический путь Р между узлами А и Z в графе G, необходимо выполнить следующие действия:

1. если А = Z, то Р = [А];

2. в противном случае найти ациклический путь Р1 от некоторого узла Y до Z, а
затем найти пути от А до Y, избегая узлов, которые входят в путь Р1.

Эта формулировка указывает на то, что требуется еще одно отношение для поиска пути с учетом ограничения, согласно которому необходимо избегать использования некоторого подмножества узлов (обозначенного выше как Р1). Поэтому определим еще одну процедуру следующим образом: pathl(A, Pathl, G, Path)

Как показано на рис.5.3, эта процедура имеет следующие параметры.

■ А — узел.

■ G — граф.

■ Pathl — путь в графе G.

■ Path — ациклический путь в графе G, который проходит от А до начала Pathl
и продолжается вдоль Pathl вплоть до его конца.

Предикаты path и pathl связаны между собой следующим отношением:

path(A, Z, G, Path):- pathl(A, [Z], G, Path).

Pathl

Path

Рис. 5. 3. Отношение pathl, где Path — путь от А до Z; последний уча­сток пути Path совпадает с Pathl

Схема, приведенная на рис. 5.3, показывает, что отношение pathl может быть определено рекурсивно. Как граничный случай может рассматриваться ситуация, при которой начальный узел пути Pathl (узел Y на рис. 5.3) совпадает с начальным узлом пути Path (узлом А). Если же начальные узлы не совпадают, то должен существовать узел X,для которого выполнится система условий:

1. Y является смежным по отношению к X (X, Y принадлежат одной дуге);

2. X не входит в состав пути Pathl;

3. Path должен соответствовать отношению pathl (А, [X | Pathl], G, Path).

Вариант фрагмента турбопрологовской программы (см. 1) в разделе clauses приводится ниже. В этой программе от­ношение member представляет собой отношение проверки принадлежности к списку. Отношение

Ad (X, Y, G) означает, что в графе G существует дуга от X до Y. Определение этого отношения за­висит от представления графа. Если G представлен в виде пары множеств (узлов и ребер) следующим образом: G = graph(V, E) то должен применяться следующий вариант этого отношения:

Ad (X, Y, graph(V,E)):-member(e(X,Y), E)

member(e(Y,X), E).

/* Поиск ациклического пути Path от а до Z в графе Graph

path(A, Z, Graph, Path): Path - ациклический путь от А до Z в графе Graph*/

Дата добавления: 2014-01-07