Скалярное произведение двух векторов

В АФФИННЫХ КООРДИНАТАХ

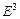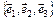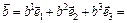
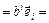
Пусть в пространстве задан базис и два произвольных вектора и 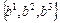. Тогда

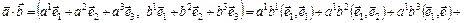
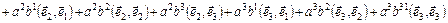
Скалярные произведения базисных векторов представляют собой некоторые числа; обозначим их через

(9.1)

В силу свойства V₁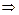

(9.2)

т.е.

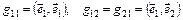
(9.3)

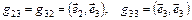
Таким образом

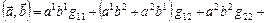
. (9.4)

Или, в обозначениях Эйнштейна:

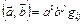(9.4^’)

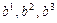Алгебраическое выражение, стоящее в правой части соотношения (9.4), представляет собой однородный многочлен от двух наборов переменных – и , линейный по каждому из этих наборов.

Вообще, однородные многочлены называют формами, а многочлены вида (4) – билинейными формами.

Так как коэффициенты 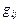обладают свойством (9.2), то билинейную форму (9.4) называют симметрической.

При (т.е. пр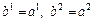и и 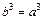) симметрическая билинейная форма превращается в однородный многочлен второй степени от переменных :

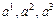. (9.5)

Многочлен (5) называют квадратичной формой. Вполне очевидно, что форма (5) однозначно определяет соответствующую симметрическую билинейную форму (т.е. коэффициенты ).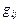

Согласно свойству V₄ при 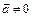форма (5) обладает свойством

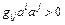(9.6)

Такие квадратичные формы (а так же соответствующие им билинейные симметрические формы) называют положительно определенными.

Таким образом, скалярное произведение двух векторов является билинейной симметрической положительно определенной квадратичной формой их координат.

Иногда форму (5) (а также и форму (4)) называют метрической, т.к. с ее помощью можно вычислять (“мерить”) длину вектора:

. (9.7)

Числа 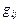определяют матрицу

, (9.8)

которая однозначно определяет как форму (4), так и форму (5), и наоборот.

Матрицу G называют метрической.

Положительная определенность квадратичной формы накладывает на коэффициенты 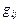(следовательно, и на матрицу G) определенные условия.

. (9.9)

¨ Требования (9.9) доказываются в курсе алгебры.

При n= 2 система координат пространства E² имеет вид 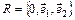. Обозначим через 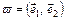угол между векторами 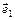и . Тогда

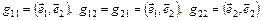, (9.10)

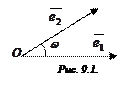
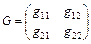(9.11)

Дата добавления: 2014-01-07