
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 11. Нелинейные функциональные уравнения. Метод Ньютона – Контаровича
Для обеспечения безопасного хранения ключей применяют их шифрование с помощью других ключей
Средства управления криптографическими ключами
Безопасность любой криптосистемы определяется используемыми криптографическими ключами. В случае ненадежного управления ключами злоумышленник может завладеть ключевой информацией и получить полный доступ ко всей информации в системе или сети.
Различают следующие виды функций управления ключами:
- генерация,
- хранение,
- и распределение ключей.
Способы генерации ключей для симметричных и асимметричных криптосистем различны.
Для генерации ключей симметричных криптосистем используются аппаратные и программные средства генерации случайных чисел.
Генерация ключей для асимметричных криптосистем более сложна, так как ключи должны обладать определенными математическими свойствами.
Функция хранения предполагает организацию безопасного хранения, учета и удаления ключевой информации.
Такой подход приводит к концепции иерархии ключей.
В иерархию ключей входит:
- главный ключ (т.е. мастер-ключ),
- ключ шифрования ключей
- и ключ шифрования данных.
Следует отметить, что генерация и хранение мастер-ключа является критическим вопросом криптозащиты.
Распределение - самый ответственный процесс в управлении ключами. Этот процесс должен гарантировать скрытность распределяемых ключей, а также быть оперативным и точным.
Между пользователями сети ключи распределяют двумя способами:
- с помощью прямого обмена сеансовыми ключами;
- используя один или несколько центров распределения ключей.
Метод Ньютона – Контаровича является одним из немногих методов нахождения решения нелинейного функционального уравнения. Приведены алгоритмы итерационного процесса Ньютона – Контаровича и доказаны две теоремы о существований и единственности решения уравнения. Рассмотрены еще два принципа существования неподвижной точки: теорема Брауэра и принцип Шаудера.
Алгоритм итерационного процесса Ньютона – Контаровича. Пусть  нелинейный оператор, переводящий открытое множество
нелинейный оператор, переводящий открытое множество  банахова пространства
банахова пространства 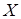 на множество из банахова пространства
на множество из банахова пространства 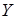 .
.
Рассмотрим нелинейное функциональное уравнение вида
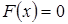 . (1)
. (1)
Предположим, что в  имеется решение
имеется решение 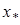 уравнения (1) т.е.
уравнения (1) т.е. 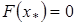 . Пусть в
. Пусть в  оператор
оператор  непрерывно дифференцируем по Фреше. Полагаем, что в
непрерывно дифференцируем по Фреше. Полагаем, что в  оператор
оператор 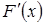 непрерывно обратим. Алгоритм итерационного процесса следующий: 1) выбирается начальная точка
непрерывно обратим. Алгоритм итерационного процесса следующий: 1) выбирается начальная точка 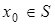 ; 2) вычислим производной Фреше оператора
; 2) вычислим производной Фреше оператора  в точке
в точке 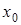 . В результате, находим оператор
. В результате, находим оператор 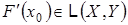 ; 3) следующее приближение
; 3) следующее приближение 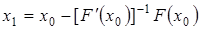 . В общем случае
. В общем случае
 . (2)
. (2)
Сходимость итерационного процесса Ньютона – Канторовича. Рассмотрим решение операторного уравнения (1) путем построения последовательности 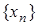 по формуле (2).
по формуле (2).
Теорема 1. Пусть оператор  дифференцируем по Фреше в шаре
дифференцируем по Фреше в шаре  , оператор
, оператор 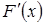 удовлетворяет условию Липшица
удовлетворяет условию Липшица
 . (3)
. (3)
Пусть оператор 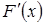 ,
, 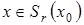 непрерывно обратим, причем
непрерывно обратим, причем
 . (4)
. (4)
Пусть 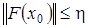 , величина
, величина  и выполнено неравенство
и выполнено неравенство 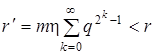 . Тогда уравнение (1) имеет решение
. Тогда уравнение (1) имеет решение 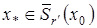 ,
, 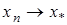 при
при  , скорость сходимости последовательность
, скорость сходимости последовательность 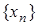 к
к 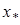 определяется по формуле
определяется по формуле
 . (5)
. (5)
Доказательство. Пусть последовательность 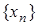 определяется по формуле (2). Покажем, что
определяется по формуле (2). Покажем, что 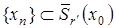 . Докажем методом математической индукции. Поскольку
. Докажем методом математической индукции. Поскольку 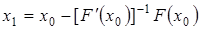 , то
, то  . Тогда
. Тогда 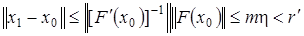 . Следовательно,
. Следовательно,  . Так как
. Так как  , то
, то  . Тогда
. Тогда 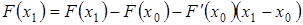 и согласно формуле (4) из леммы (10), имеем
и согласно формуле (4) из леммы (10), имеем
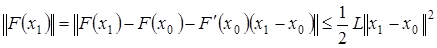 .
.
Итак, включение 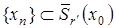 верно для значений
верно для значений 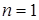 .
.
Полагаем, что включение 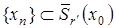 верно для значений
верно для значений 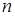 , причем
, причем
 . (6)
. (6)
Докажем, что
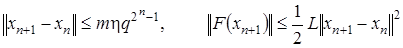 . (7)
. (7)
Из (4), (6) имеем

Отсюда следует первое неравенство из (7). Так как 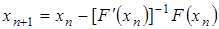 , то
, то 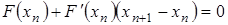 . Тогда
. Тогда
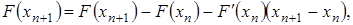
 .
.
Следовательно, верно второе неравенство из (7). Доказано, что 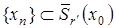 .
.
Покажем, что последовательность 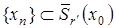 фундаментальна. Как следует из формулы (7), верна оценка
фундаментальна. Как следует из формулы (7), верна оценка
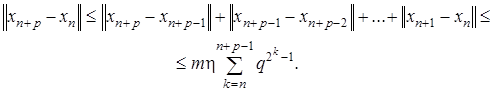 (8)
(8)
Тогда 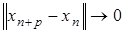 при
при  для любого конечного
для любого конечного 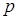 . Следовательно, последовательность
. Следовательно, последовательность 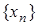 – фундаментальна, а в силу того, что
– фундаментальна, а в силу того, что 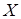 – банахово пространство, последовательность
– банахово пространство, последовательность 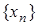 сходится. Пусть
сходится. Пусть 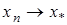 при
при  . Так как
. Так как 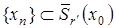 , то
, то 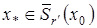 .
.
Покажем, что 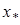 – решение уравнения
– решение уравнения 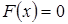 . Поскольку
. Поскольку 
 , то при
, то при  имеем
имеем  . Отсюда имеем
. Отсюда имеем 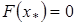 .
.
Из оценки (8) при фиксированном 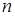 и при
и при  , получим
, получим
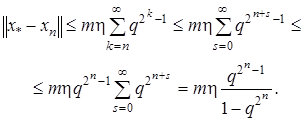
теорема доказана.
Примечательно то, что существование решения операторного уравнения 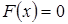 следует из утверждения теоремы, не исключается возможность того, что уравнение
следует из утверждения теоремы, не исключается возможность того, что уравнение 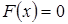 может иметь не единственное решение в замкнутом шаре
может иметь не единственное решение в замкнутом шаре 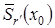 .
.
Модифицированный метод Ньютона – Канторовича. Метод построения последовательности  по формуле (2) требует вычисления обратного оператора
по формуле (2) требует вычисления обратного оператора 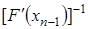 на каждой итерации. Рассмотрим следующую модификацию метода Ньютона – Канторовича
на каждой итерации. Рассмотрим следующую модификацию метода Ньютона – Канторовича
 (9)
(9)
Отличие (9) от (2) состоит в том, что обратный оператор определяется только в начальной точке 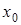 .
.
Теорема 2. Пусть выполнены следующие условия:
1) оператор  дифференцируем по Фреше в шаре
дифференцируем по Фреше в шаре  и
и
 ;
;
2) существует обратный оператор 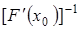 , причем
, причем 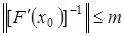 ;
;
3) 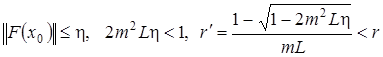 .
.
Тогда уравнение 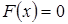 имеет единственное решение
имеет единственное решение 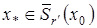 ,
, 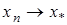 при
при  . Справедлива следующая оценка скорости сходимости
. Справедлива следующая оценка скорости сходимости
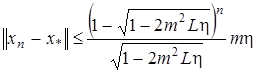 .
.
Доказательство. Пусть оператор  . Покажем, что оператор
. Покажем, что оператор 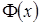 отображает замкнутый шар
отображает замкнутый шар 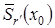 в себя. В самом деле,
в себя. В самом деле,
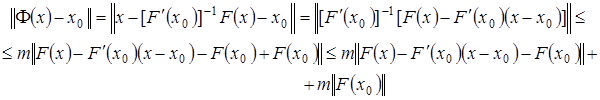
Отсюда, используя лемму 5 из лекции 10 (см. формулу (4)), имеем
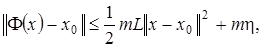
где 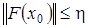 . Так как,
. Так как,  , то
, то  . Следовательно,
. Следовательно,  . Поскольку
. Поскольку  , то
, то 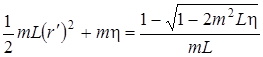 . Тогда
. Тогда  , оператор
, оператор 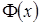 отображает
отображает 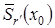 в себя.
в себя.
Докажем, что оператор 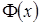 является сжимающим в
является сжимающим в 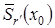 . Как следует из теоремы 6 лекции 10 (см. следствие 3), норма
. Как следует из теоремы 6 лекции 10 (см. следствие 3), норма

следовательно,  , оператор
, оператор  является сжимающим.
является сжимающим.
Таким образом, оператор 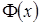 удовлетворяет условиям теоремы 6 лекции 5 и верны утверждения 1) – 3). Из утверждения 1) следует, что оператор
удовлетворяет условиям теоремы 6 лекции 5 и верны утверждения 1) – 3). Из утверждения 1) следует, что оператор 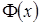 имеет единственную неподвижную точку
имеет единственную неподвижную точку 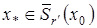 т.е
т.е  . Так как
. Так как 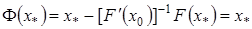 , то
, то 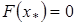 . Следовательно,
. Следовательно, 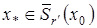 является решением уравнения
является решением уравнения 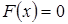 . Поскольку
. Поскольку  , то
, то 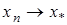 при
при  . Далее, величина
. Далее, величина  , то верна оценка
, то верна оценка
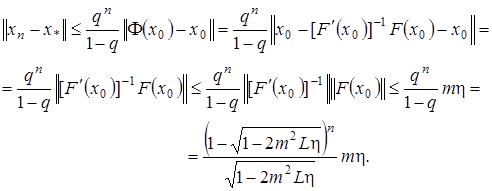
Теорема доказана.
Теорема Брауэра. Отметим, что: 1) пусть 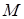 – некоторое множество в банаховом пространстве
– некоторое множество в банаховом пространстве  , состоящее из конечного числа элементов т.е.
, состоящее из конечного числа элементов т.е. 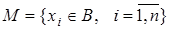 , множество
, множество 
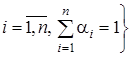 называется выпуклой оболочкой множества
называется выпуклой оболочкой множества 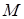 и обозначается
и обозначается 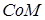 ; 2) выпуклым телом в банаховом пространстве
; 2) выпуклым телом в банаховом пространстве  называется выпуклое замкнутое множество, имеющее хоть одну внутреннюю точку.
называется выпуклое замкнутое множество, имеющее хоть одну внутреннюю точку.
Теорема 3. Пусть 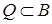 ,
,  – выпуклое ограниченное тело
– выпуклое ограниченное тело 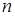 –мерного банахова пространства
–мерного банахова пространства  . Тогда любой непрерывный оператор
. Тогда любой непрерывный оператор  ,
,  , отображающий множество
, отображающий множество  в себя, имеет в
в себя, имеет в  неподвижную точку.
неподвижную точку.
Пример 1. Пусть  – непрерывная функция, отображающая
– непрерывная функция, отображающая  в себя т.е
в себя т.е  . Покажем, что
. Покажем, что  имеет неподвижную точку в
имеет неподвижную точку в  т.е
т.е 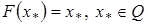 . В самом деле, функция
. В самом деле, функция 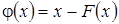 ,
,  обладает свойствами
обладает свойствами  ,
, 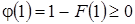 . Заметим, что: 1) если
. Заметим, что: 1) если  или
или  , то
, то  или
или  ; 2) если
; 2) если 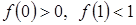 , то
, то 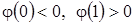 . Согласно теореме о промежуточных значениях непрерывной функции найдется точка
. Согласно теореме о промежуточных значениях непрерывной функции найдется точка  такая, что
такая, что  . Тогда
. Тогда 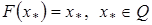 , где
, где 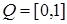 – выпуклое ограниченное тело в
– выпуклое ограниченное тело в 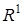 .
.
Принцип неподвижной точки Шаудера. Обобщением теоремы Брауэра является принцип неподвижной точки Шаудера. Теорема Брауэра не пригодна для решения многих задач функционального анализа из-за конечномерности множества  .
.
Определение 1. Пусть  – банаховы пространства,
– банаховы пространства, 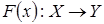 ,
,  ,
,  . Оператор
. Оператор  называется вполне непрерывным на
называется вполне непрерывным на 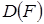 , если он непрерывен на
, если он непрерывен на 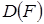 и любое ограниченное множество из
и любое ограниченное множество из 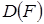 переводит в компактное множество в
переводит в компактное множество в 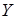 .
.
Отметим, что: 1) если 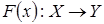 – непрерывный оператор,
– непрерывный оператор,  – конечномерные банаховы пространства, то
– конечномерные банаховы пространства, то  вполне непрерывный оператор; 2) если
вполне непрерывный оператор; 2) если 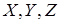 – банаховы пространства,
– банаховы пространства, 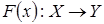 – ограниченный непрерывный оператор,
– ограниченный непрерывный оператор, 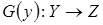 – линейный вполне непрерывный оператор, то
– линейный вполне непрерывный оператор, то  – вполне непрерывный оператор; 3) оператор
– вполне непрерывный оператор; 3) оператор  . Пусть оператор
. Пусть оператор 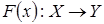 непрерывен в ограниченном множестве
непрерывен в ограниченном множестве 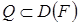 , множество
, множество  компактно, где
компактно, где 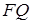 – образ множества
– образ множества  . Из компактности
. Из компактности 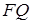 , согласно критерию Хаусдорфа, следует, что существует для любого
, согласно критерию Хаусдорфа, следует, что существует для любого  конечная
конечная 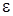 – сеть
– сеть 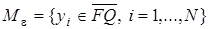 множества
множества 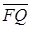 , где
, где 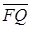 – замыкания множества
– замыкания множества 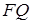 .
.
Определим оператор 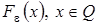 следующим образом
следующим образом
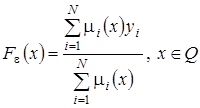 .
.
где 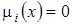 , если
, если 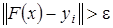 ;
;  , если
, если 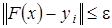 . Оператор
. Оператор  называется
называется 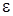 – проектором Шаудера. Можно показать, что оператор
– проектором Шаудера. Можно показать, что оператор  ,
,  непрерывен.
непрерывен.
Покажем, что 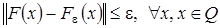 . Так как
. Так как
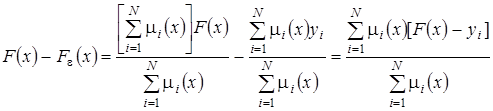 ,
,
то
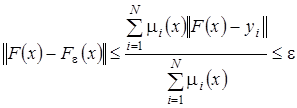 ,
,
в силу того, что 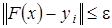 ,
,  . Отсюда следует, что оператор
. Отсюда следует, что оператор  аппроксимирует оператор
аппроксимирует оператор  на
на  с точностью
с точностью 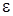 .
.
При построении оператора  вместо конечной
вместо конечной 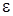 –сети Хаусдорфа, можно взять конечную
–сети Хаусдорфа, можно взять конечную 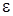 –сеть любого компактного множества, содержащего
–сеть любого компактного множества, содержащего 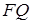 . Таким образом оператор
. Таким образом оператор  можно аппроксимировать оператором
можно аппроксимировать оператором  ,
,  .
.
Теорема 4. (принцип Шаудера). Пусть  – замкнутое ограниченное выпуклое множество банахова пространства
– замкнутое ограниченное выпуклое множество банахова пространства 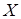 , оператор
, оператор 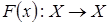 отображает
отображает  в себя и является вполне непрерывным на
в себя и является вполне непрерывным на  . Тогда оператор
. Тогда оператор  имеет неподвижную точку на
имеет неподвижную точку на  .
.
Доказательство. Предположим противное т.е. оператор  не имеет неподвижную точку на
не имеет неподвижную точку на  . Тогда существует число
. Тогда существует число 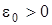 такое, что
такое, что 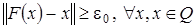 . Так как оператор
. Так как оператор  вполне непрерывен, то множество
вполне непрерывен, то множество 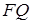 – компактно.
– компактно.
Отметим, что если не выполнено неравенство  , то оператор
, то оператор  имеет неподвижную точку на
имеет неподвижную точку на  . В самом деле, существует последовательность
. В самом деле, существует последовательность  такая, что
такая, что  при
при  , где
, где 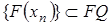 . Так как множество
. Так как множество 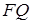 – компактно, то из
– компактно, то из 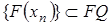 можно выделить последовательность
можно выделить последовательность 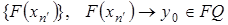 . Тогда
. Тогда  , в силу того, что
, в силу того, что  при
при 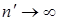 . Следовательно,
. Следовательно,  , что противоречит предположению оператор
, что противоречит предположению оператор  не имеет неподвижную точку на
не имеет неподвижную точку на  .
.
Пусть число 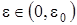 . Пусть
. Пусть  – конечная
– конечная 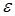 –сеть множества
–сеть множества 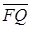 . Выделим из
. Выделим из 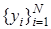 – максимальную линейно независимую систему элементов
– максимальную линейно независимую систему элементов 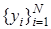 ,
, 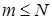 . Пусть
. Пусть 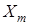 подпространство в
подпространство в 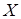 натянутое на элементы
натянутое на элементы 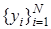 . Подпространство
. Подпространство 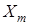 является
является  –мерным банаховым пространством и оно содержит элемент
–мерным банаховым пространством и оно содержит элемент  .
.
Обозначим через  . Множество
. Множество  ,
, 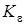 является выпуклым телом,
является выпуклым телом,  , в силу того, что
, в силу того, что 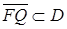 .
.
Пусть 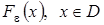 –
– 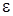 –проектор Шаудера. Рассмотрим сужение оператора
–проектор Шаудера. Рассмотрим сужение оператора  на множество
на множество 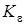 т.е.
т.е.  ,
,  . Для оператора
. Для оператора  ,
, 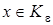 применим теорема Брауэра. Согласно теореме Брауэра, оператор
применим теорема Брауэра. Согласно теореме Брауэра, оператор  имеет неподвижную точку
имеет неподвижную точку  т.е.
т.е. 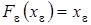 . Тогда
. Тогда 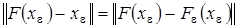 . Так как оператор
. Так как оператор 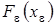 является
является 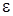 аппроксимацией оператора
аппроксимацией оператора 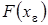 , то
, то 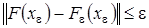 . Итак, имеем
. Итак, имеем 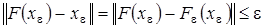 . Это противоречит неравенству
. Это противоречит неравенству 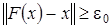 ,
, 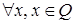 , где
, где 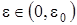 . Следовательно, предположение о том, что
. Следовательно, предположение о том, что  не имеет неподвижную точку на
не имеет неподвижную точку на  не верно. Теорема доказана.
не верно. Теорема доказана.
|
Дата добавления: 2014-01-07; Просмотров: 1468; Нарушение авторских прав?; Мы поможем в написании вашей работы!