Методы измерений

Классификация измерений

Под термином "измерение" понимают совокупность операций, выполняемых для определения количественного значения величины (Федеральный закон "Об обеспечении единства измерений").

Процесс измерения состоит из ряда взаимосвязанных и последовательных этапов (рис. 1).

Рис. 1. - Основные элементы и этапы процесса измерения

Все измерения классифицируют:

- по общим приёмам получения результатов измерений;

- по характеру изменения получаемой информации в процессе измерения;

- по количеству измерительной информации;

- по отношению к основным единицам.

1. По общим приёмам получения результатов измерения делятся на:

- прямые,

- косвенные,

- совокупные,

- совместные.

При прямых измерениях искомое значение измеряемой величины получают непосредственно из опытных данных (сравнением величины с ее единицей).

То есть объект исследования приводят во взаимодействие со средством измерений и по его показаниям отсчитывают значение измеряемой величины.

Часто под прямыми понимаются такие измерения, при которых не производится промежуточных преобразований.

К прямым измерениям относятся: измерение массы при помощи весов и гирь, измерение длины - линейкой, давления - манометром, силы тока - амперметром, температуры - термометром, измерение напряжения - вольтметром, сопротивления - омметром, мощности - ваттметром и т.д.

При косвенных измерениях искомое значение величины определяют на основании прямых измерений других величин, функционально связанных известной зависимостью с искомой величиной.

При этом числовое значение искомой величины определяется по формуле:

z = F(a₁, a₂, …, a_m),

где z - искомое значение измеряемой величины,

a₁, a₂, …, a_m - результаты прямых измерений величин, связанных зависимостью F с искомым значением.

Примеры: определение значения активного сопротивления R резистора на основе прямых измерений силы тока I через резистор и падения напряжения U на нём по формуле R = U/I; измерение мощности методом амперметра-вольтметра и др.

К косвенным относятся те измерения, при которых расчёт осуществляют вручную или автоматически, но после получения результатов прямых измерений. При этом может быть учтена отдельно погрешность расчёта значений.

Косвенные измерения сложнее прямых, однако они широко применяются в практике либо потому, что прямые измерения практически невыполнимы, либо потому, что косвенное измерение позволяет получить более точный результат по сравнению с прямым измерением.

При совокупных измерениях одновременно проводятся измерения нескольких одноименных величин, и искомое значение величины определяют решением системы уравнений, получаемых при измерениях этих величин в различных сочетаниях; при этом число уравнений должно быть не меньше числа величин.

Например, значение массы отдельных гирь набора можно определить по известному значению массы одной из гирь и по результатам измерений (сравнений) масс различных сочетаний гирь.

Или, измеряя сопротивления R_ab, R_ac и R_bc между вершинами треугольника, в котором соединены сопротивления R₁, R₂ и R₃ (см. схему), и решая полученную систему уравнений, можно определить искомые значения сопротивлений R₁, R₂ и R₃:

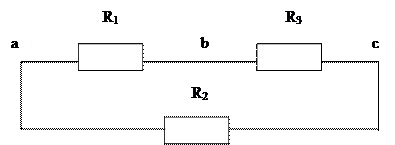R_ab = R₁(R₂ + R₃)/(R₁ + R₂ + R₃),

R_ac = R₂(R₁ + R₃)/(R₁ + R₂ + R₃),

R_bc = R₃(R₁ + R₂)/(R₁ + R₂ + R₃).

Совместные - производимые одновременно измерения двух или нескольких неодноимённых величин для установления зависимости между ними.

Характерный пример совместных измерений - определение зависимости сопротивления резистора от температуры:

R_t = R₂₀[1 + α(t-20) + β(t-20)²],

где R₂₀ - сопротивление резистора при t = 20ºC; α и β -температурные коэффициенты.

Для определения величин R₂₀, α и β измеряют сопротивление R_t резистора при трёх различных значениях температуры, затем составляют систему из трёх уравнений, по которой находят искомые параметры:

R_t1 = R₂₀[1 + α(t₁-20) + β(t₁-20)²],

R_t2 = R₂₀[1 + α(t₂-20) + β(t₂-20)²],

R_t3 = R₂₀[1 + α(t₃-20) + β(t₃-20)²].

Совокупные и совместные измерения весьма близки друг к другу.

Числовые значения искомых величин при совокупных и совместных измерениях определяются из системы уравнений, коэффициенты в которых получены прямыми (или косвенными) измерениями.

Отличие состоит в том, что при совокупных измерениях одновременно определяют несколько одноимённых величин, а при совместных - разноимённых.

Косвенные, совместные и совокупные измерения объединяются одним принципиально важным общим свойством: их результаты рассчитываются по известным функциональным зависимостям между измеряемыми величинами и величинами, определяемыми прямыми измерениями.

Различие между этими видами измерений заключается только в виде функциональной зависимости, используемой при расчётах.

При косвенных измерениях она выражается одним уравнением в явном виде, а при совместных и совокупных - системой неявных уравнений.

2. По характеру изменения получаемой информации в процессе измерений измерения подразделяются на статические и динамические.

Любое средство измерений, как материальная система, обладает инерцией (механической, тепловой, электрической) и, следовательно, не может мгновенно реагировать на изменение измеряемой величины.

Поэтому при измерении переменной физической величины инерция средства измерения приведет к некоторому отставаниюпоказаний средства измерения от истинного значения величины в каждый момент времени.

Очевидно, что это отставание будет зависеть не только от инерционных (динамических) свойств средств измерений, но и от скорости изменения самой измеряемой величины.

В том случае, когда показания средства измерения не зависят от его динамических свойств или когда этой зависимостью можно пренебречь, говорят, что средство измерения работает в статическом режиме, а само измерение называют статическим.

В противном случае измерение относят к динамическим.

Таким образом, статические измерения - это такие измерения, когда измеряемая величина принимается за неизменную на протяжении времени измерения; например, измерение размеров земельного участка, измерение постоянного тока в цепи и др.

Динамические измерения - это измерения, в процессе которых измеряемая величина изменяется.

Развитие средств измерений и повышение их чувствительности позволяет сегодня обнаружить изменение величин, ранее считавшихся постоянными, поэтому разделение измерений на динамические и статические можно считать условным.

3. По количеству измерительной информации измерения делятся на однократные ( простые)и многократные (статистические).

Однократные измерения выполняются один раз, а многократные позволяют получить результат из нескольких следующих друг за другом измерений одного и того же объекта.

При однократных измерениях показания средства измерений являются результатом измерений; погрешность используемого средства измерений определяет погрешность результата измерения.

Применение многократных измерений позволяет повысить точность измерения до определенного предела.

4. По отношению к основным единицам измерения делятся на абсолютные и относительные.

Абсолютные измерения основаны на прямых измерениях одной или нескольких основных величин или использовании значений физических констант.

Например, определение массы в килограммах, количества вещества - в молях, частоты - в герцах.

Результат абсолютного измерения непосредственно выражается в единицах измеряемой величины.

Относительные измерения - это измерения отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную.

Например, относительная влажность определяется как отношение упругости водяного пара, содержащегося в воздухе, к упругости насыщенного пара при той же температуре, и выражается в процентах; сюда же относятся измерения отношения напряжений или мощностей, исследование частотных характеристик (коэффициентов передачи) электрических цепей и т.д.

Относительные измерения при прочих равных условиях могут быть выполнены более точно, чем абсолютные, так как в суммарную погрешность не входит погрешность меры величины.

При относительных измерениях используют внесистемную безразмерную единицу - децибел (дБ), определяемую при сравнении напряжений U₁ и U₂ по формуле

1дБ = 20lg(U₂/ U₁),

а при сравнении мощностей P₁ и P₂:

1дБ = 10lg(P₂/ P₁).

Последовательность операций выполнения измерений, правила и приемы, позволяющие получить результат с требуемой точностью, излагаются в документе, который называется методикой выполнения измерений (МВИ).

Измерения, относящиеся к сфере государственного обеспечения единства измерений, должны выполняться по аттестованным методикам измерений.

Результаты измерений должны быть выражены в единицах величин, допускаемых к применению в Российской Федерации.

Сбор сведений об аттестованных методиках измерений ведет Федеральный информационный фонд по обеспечению единства измерений.

Приведем определения основных характеристик измерений.

Любое измерение представляет собой физический эксперимент, выполнение которого основано на использовании тех или иных физических явлений.

Совокупностьфизических явлений, на которых основаны измерения, называется принципом измерения.

Например, применение эффекта Доплера для измерения скорости движения звезд, вращения небесных тел.

Метод измерений - прием или совокупность приемов сравнения измеряемой величины с ее единицей в соответствии с реализованным принципом измерений.

Например, проведение измерений с помощью ядерного магнитного резонанса (магнитные измерения); электронная спектроскопия (оптические измерения) и др.

Каждую физическую величину можно измерить несколькими методами, которые могут отличаться друг от друга особенностями как технического, так и методического характера.

В отношении технических особенностей можно сказать, что существует множество методов измерения, и по мере развития науки и техники число их всё увеличивается.

С методической стороны все методы измерений поддаются систематизации и обобщению по общим характерным признакам.

Различные методы измерений отличаются прежде всего организацией сравнения измеряемой величины с единицей измерения.

С этой точки зрения все методы измерений подразделяются на две группы:

- метод непосредственной оценки и

- методы сравнения.

Метод непосредственной оценки позволяет определить значение величины по отсчетному устройству средства измерения, которое заранее проградуировано в единицах измеряемой величины или в единицах других величин, от которых она зависит.

На этом методе основаны все показывающие (стрелочные) приборы (вольтметры, амперметры, ваттметры, счётчики энергии, термометры, тахометры и т.д.).

В методе непосредственной оценки мера в явном виде при измерении не присутствует, ее размеры перенесены на отсчётное устройство (шкалу) средства измерения заранее, при его градуировке.

Быстрота процесса измерения методом непосредственной оценки делает его часто незаменимым для практического использования, хотя точность измерений в большинстве случаев невелика.

Метод сравнения с мерой - метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.

Примеры: измерение массы на рычажных весах с уравновешиванием гирь; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС нормального элемента и др.

Отличительная черта методов сравнения - непосредственное участие меры в процедуре измерения.

Обязательным в методе сравнения является наличие сравнивающего устройства.

Различают следующие разновидности метода сравнения.

Дифференциальный метод - метод сравнения с мерой, в котором на измерительный прибор воздействует разностьизмеряемой величины и известной величины, воспроизводимой мерой.

Пример: измерение массы на равноплечих весах, когда воздействие массы m_x на весы частично уравновешивается массой гирь m₀, а разность масс отсчитывается по шкале весов, градуированной в единицах массы.

В этом случае значение измеряемой величины m_x = m₀ + Δm, где Δm - показания весов.

Этот метод позволяет получить результат измерений с высокой точностью даже в случае применения относительно неточных измерительных приборов, если с большой точностью воспроизводится известная величина.

Пример. Необходимо измерить постоянное напряжение, истинное значение которого равно U_x = 0,99 В.

В распоряжении экспериментатора имеется набор вольтметров (или один многопредельный) с пределами измерения 0,01; 0,1 и 1 В.

Пусть погрешность каждого вольтметра при измерении величины, значение которой равно пределу измерения, составляет 1%.

Предположим, имеется образцовая мера напряжения U = 1 В, погрешность которой пренебрежимо мала.

Очевидно, что производя измерения методом непосредственной оценки, экспериментатор использует вольтметр с пределом измерения 1 В и получает результат измерения с погрешностью 1%.

При дифференциальном методе измерения экспериментатор включает источники измеряемого постоянного напряжения U_x и образцового напряжения U_o последовательно и встречно и измеряет их разность U_o - U_x = 0,01 В вольтметром с пределом измерения 0,01 В.

В этом случае разность U_o - U_x будет измерена с погрешностью 1%, а следовательно, значение напряжения будет определено с погрешностью 0,01%.

Эффект повышения точности результатов измерений, достигаемый при дифференциальном методе, тем значительнее, чем ближе значение меры к истинному значению измеряемой величины.

Когда результирующий эффект воздействия величин на прибор сравнения доводят до нуля, дифференциальный метод измерений превращается в нулевой.

Очевидно, что в нулевом методе измерений используемая мера должна быть изменяемой (регулируемой), а прибор сравнения выполняет функции индикатора равенства нулю результирующего воздействия измеряемой величины и меры.

Нулевой метод позволяет получить высокие точности измерений.

Он используется, например, при измерении массы на равноплечих весах, когда воздействие на весы массы m_x полностью уравновешивается массой гирь m₀; при измерениях электрического сопротивления мостом с полным его уравновешиванием или постоянного напряжения компенсатором постоянного тока.

Метод замещения - метод сравнения с мерой, в котором измеряемую величину замещаютизвестной величиной, воспроизводимой мерой.

Пример: взвешивание на пружинных весах. Измерение производят в два приема. Вначале на чашу весов помещают взвешиваемую массу и отмечают положение указателя весов; затем массу m_x замещают массой гирь m₀, подбирая ее так, чтобы указатель весов установился точно в том же положении, что и в первом случае. При этом ясно, что m_x = m₀.

Метод замещения можно рассматривать как разновидность дифференциального или нулевого, отличающуюся тем, что сравнение измеряемой величины с мерой производится разновременно.

Метод совпадений - метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадения отметок шкал или периодических сигналов.

Пример: измерение числа оборотов вала с помощью стробоскопа. Вал периодически освещается вспышками света, и частоту вспышек подбирают так, чтобы метка, нанесенная на вал, казалась наблюдателю неподвижной.

Метод совпадений, использующий совпадения основной и нониусной отметок шкал, реализуется также в штангенприборах, применяемых для измерений линейных размеров.

Различия в методах сравнения измеряемой величины с мерой находят отражение в принципах построения измерительных приборов.

С этой точки зрения различают измерительные приборыпрямого действия и приборы сравнения.

В измерительном приборе прямого действия предусмотрено одно или несколько преобразований сигнала измерительной информации в одном направлении, т.е. без применения обратной связи.

Пример: структурная схема электронного вольтметра

В - выпрямитель

УПТ - усилитель постоянного тока

ИМ - измерительный механизм

Характерная особенность приборов прямого действия - потребление энергии от объекта измерения.

Измерительный прибор сравнения предназначен для непосредственного сравнения измеряемой величины с величиной, значение которой известно.

Пример: структурная схема автоматического прибора сравнения:

УС - устройство сравнения

УУ - устройство управления

М - изменяемая (регулируемая) мера с отсчётным устройством

В зависимости от результата сравнения х с х₀ устройство управления УУ воздействует на меру М таким образом, чтобы величина |х - х₀| уменьшалась. Процесс уравновешивания заканчивается, когда х₀ = х.

Значение измеряемой величины отсчитывается по шкале регулируемой меры.

Очевидно, что любой измерительный прибор сравнения должен иметь цепь обратной связи и замкнутую структуру.

В измерительных приборах сравнения в цепи обратной связи всегда формируется физическая величина, однородная с измеряемой, которая подаётся на вход прибора.

Сравнение измеряемой величины с мерой в приборах сравнения может осуществляться либо одновременно (нулевой метод), либо разновременно (метод замещения).

Дата добавления: 2014-01-07