Свойства задачи Коши

Точность и устойчивость

Прежде чем выбрать метод решения какой-либо вычислительной задачи, необходимо исследовать свойства этой задачи, т.к. в неустойчивых задачах наличие даже малых погрешностей вносит большое искажение в решение и даже самый лучший численный метод не может исправить положение. В задаче Коши исследованию подлежат два типа устойчивости: по начальному условию и по правой части.

Устойчивость по начальному условию. Пусть у₀ – некое начальное условие задачи (5.2), а = у₀ – e₀ – возмущённое начальное условие, т.е. заданное с погрешностью e₀. Определим, приведёт ли эта погрешность в начальных условиях к накоплению ошибки в решении.

Пусть

– (5.8)

возмущённая задача Коши, т.е. с погрешностью в начальном условии. Вычтем из уравнения (5.2) уравнение (5.8):

= f(x, y) – f(x, y*).

Воспользуемся формулой конечных приращений Лагранжа, которая для произвольной функции g(x) и произвольных значений аргумента x = a и x = b имеет вид: , где сÎ(a, b) – некоторая точка, наклон касательной в которой равен наклону секущей, проходящей через точки a и b (см. рисунок).

Применим формулу Лагранжа к функции f(x, y), полагая a = y(x), b = y*(x), c =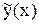Î(y(x), y*(x)):

f(x, y(x)) – f(x, y*(x)) = ×[y(x) – y*(x)].

Отсюда имеем дифференциальное уравнение относительно 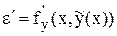e:

×e

с начальным условием e(x₀) = y₀ – = e₀. Полученное уравнение является линейным однородным, его решение имеет вид:

e(x) = e₀×exp= e₀×C(x).

Здесь C(x) – коэффициент роста ошибки с увеличением х. Если > 0, то показатель экспоненты также положителен и С(х) возрастает. Вместе с ним растёт и погрешность решения. При < 0 получим, что С(х) убывает, а погрешность решения затухает. Если меняет знак, то проанализировать рост ошибки сложно.

Пример 5.4. Пусть имеем задачу Коши

.

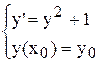f(x, y) = y² +1, следовательно = 2у. При у > 0 будет > 0 и погрешность возрастает, а при у < 0 будет < 0 и погрешность убывает. Проверим это. Точное решение этой задачи у = tg[(x – x₀) + arctg(y₀)]. Рассмотрим два случая.

1. x₀ = 0, xÎ[0; 1.3]. Пусть у₀ = 0, e₀ = –0.1, т.е. 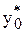= 0.1. Тогда y(x) = tg(x), y*(x) = tg(x+0.099669). y ³0. Графики обеих кривых – на рисунке. Видно, что линии расходятся, т.е. погрешность возрастает.

– точное решение – возмущённое решение

2. x₀ = –1.3, xÎ[–1.3; 0]. Пусть у₀ = tg(–1.3) = –3.602102, а e₀ = –0.7, т.е. 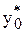= tg(–1.3)+0.7 = – 2.9021. Тогда y(x) = tg(x), y*(x) = tg(x+1.3+arctg(– 2.9021)) = tg(x+0.061). y < 0. Графики обеих кривых – на рисунке. Видно, что линии сходятся, т.е. погрешность убывает.

– точное решение – возмущённое решение

В обоих случаях если область [x₀, x_N] решения дифференциального уравнения конечна, то при достаточно малом e₀ можно ожидать, что С(х) не возрастёт слишком сильно, т.е. погрешность решения не будет очень большой.

Устойчивость по правой части. Пусть правая часть f(x, y) уравнения (5.2) при произвольном х вычисляется с погрешностью y(х), т.е. имеем следующую возмущённую задачу:

(5.9)

Поведение решения задачи (5.9) определяется следующей теоремой:

Теорема 5.1 (об устойчивости по правой части). Если функция f(x, y) удовлетворяет условию Липшица:

$ L > 0: " y₁, y₂, " x | f(x, y₁) – f(x, y₂) | £ L×| y₁ – y₂ |,

то для решения y(x) задачи (5.2) и решения y*(x) задачи (5.9) справедлива оценка:

.

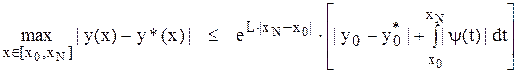Это означает, что если отрезок [x₀, x_N] конечен, то при достаточно малой величине 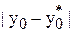и | y(x) | разницу | y(x) – y*(x) | можно также сделать малой, т.е. решение устойчиво. Значения 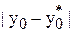и | y(x) | представляют собой погрешности исходных данных, а | y(x) – y*(x) | – погрешность решения. Следовательно, величина является оценкой числа обусловленности задачи Коши.

Дата добавления: 2014-01-07