
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Численные методы интегрирования
|
|
|
|
2.1. Метод прямоугольников
Использует простейшую кусочно-ступенчатую аппроксимацию подинтегральной функции  на элементарных отрезках, заменяя ее постоянным значением
на элементарных отрезках, заменяя ее постоянным значением 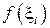 . В качестве точек
. В качестве точек 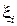 можно принять левые
можно принять левые 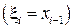 , правые
, правые 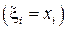 границы или середину
границы или середину  элементарных отрезков. При этом интеграл заменяется интегральной суммой:
элементарных отрезков. При этом интеграл заменяется интегральной суммой: 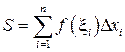 .
.
При 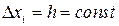 , например для метода прямоугольников, имеем:
, например для метода прямоугольников, имеем:
 .
.
2.2. Метод трапеций
Использует кусочно-линейную аппроксимацию функции 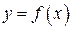 по двум граничным точкам на каждом элементарном отрезке. Интеграл представляет собой сумму площадей элементарных трапеций:
по двум граничным точкам на каждом элементарном отрезке. Интеграл представляет собой сумму площадей элементарных трапеций:
 ,
,
где  .
.
2.3. Метод Симпсона
Отрезок интегрирования  разобьем на четное число
разобьем на четное число 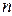 равных частей с шагом
равных частей с шагом 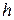 . На каждом элементарном отрезке
. На каждом элементарном отрезке 
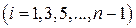 подынтегральную функцию
подынтегральную функцию аппроксимируем многочленом Лагранжа 2-й степени (через 3-и точки можно провести единственную параболу). Элементарная площадь
аппроксимируем многочленом Лагранжа 2-й степени (через 3-и точки можно провести единственную параболу). Элементарная площадь 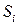 может быть вычислена с помощью определенного интеграла:
может быть вычислена с помощью определенного интеграла: 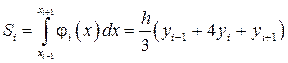 , где
, где  – полином Лагранжа;
– полином Лагранжа;
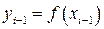 ;
;  ;
;  . После суммирования
. После суммирования  имеем:
имеем:

2.4. Погрешность численного интегрирования
Погрешность численного интегрирования равна:
численного интегрирования равна: и зависит от шага разбиения h интервала
и зависит от шага разбиения h интервала 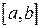 . Её можно представить в виде
. Её можно представить в виде  ─ порядка k (
─ порядка k ( ). Из этого следует, что при
). Из этого следует, что при 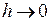 ,
, 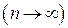 значения интеграла, получаемые путем численного интегрирования, сходятся к его точному значению.
значения интеграла, получаемые путем численного интегрирования, сходятся к его точному значению.
Главный член погрешности  формулы прямоугольников на каждом элементарном отрезке
формулы прямоугольников на каждом элементарном отрезке 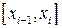 равен
равен 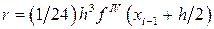 , для формулы трапеций
, для формулы трапеций  . Главный член погрешности метода Симпсона имеет вид
. Главный член погрешности метода Симпсона имеет вид  , из чего следует, что метод Симпсона дает погрешность вычисления площади на каждом отрезке
, из чего следует, что метод Симпсона дает погрешность вычисления площади на каждом отрезке 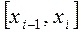 ~ в h /7,5 меньшую, чем метод прямоугольников.
~ в h /7,5 меньшую, чем метод прямоугольников.
При равноых интервале интегрирования  и числе его разбиения n на элементарные отрезки метод прямоугольников имеет ошибку вычисления интеграла равную
и числе его разбиения n на элементарные отрезки метод прямоугольников имеет ошибку вычисления интеграла равную  ,
,
|
|
|
а метод Симпсона (парабол)  т.е. на порядок меньшую.
т.е. на порядок меньшую.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 214; Нарушение авторских прав?; Мы поможем в написании вашей работы!