Определение взаимного расположения прямых по их уравнениям

Способы задания прямой на плоскости

ПРЯМАЯ НА ПЛОСКОСТИ

Какие особенности психомоторного развития вы заметили у продемонстрированных в этой лекции детей, истории болезни которых приведены в настоящей лекции?

3. Какая коррекционная работа, по Ввашему мнению, им необходима? детям, истории болезни которых приведены в настоящем разделе?

В этом параграфе мы рассмотрим различные варианты задания прямых на плоскости и приведем формулы и утверждения, позволяющие решать основные задачи, связанные с прямыми на плоскости. Материал параграфа разобьем на несколько пунктов.

Прямую на плоскости 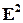можно задавать различными способами. Например, на прямой можно зафиксировать некоторую точку 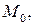которую будем называть начальной точкой прямой, и выбрать ненулевой вектор этой прямой, который будем называть направляющим вектором прямой. Тогда необходимое и достаточное условие того, что точка 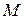лежит на прямой формулируется следующим образом:

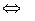(векторы и коллинеарны) (рис. 1).

Рис. 1

Пусть – фиксированная точка плоскости, 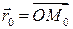– радиус-вектор начальн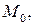ой точки – радиус-вектор произвольной точки 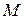плоскости. Коллинеарность векторов и означает, что для некоторого Учитывая, что 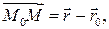имеем следующую цепочку эквивалентностей:

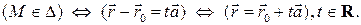
Таким образом, мы получили векторно-параметрическое задание прямой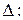

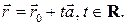(1)

По формуле (1) можно найти радиус-вектор любой точки прямой в зависимости от значения параметра (рис. 2).

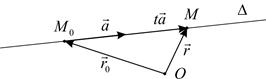
Рис. 2

Равенство (1) называют также векторно-параметрическим уравнением прямой

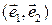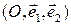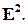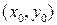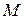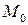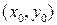Присоединим к точке базис множества векторов плоскости получим аффинный репер на плоскости Пусть и – координаты соответственно точек и в данном репере. Согласно определения 2.1.2, и – координаты соответственно радиус-векторов и в базисе Пусть – координаты направляющего вектора прямой в базисе Тогда векторное равенство (1) равносильно двум скалярным равенствам:

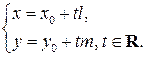(2)

Формулы (2) выражают координатно-параметрическое задание прямой, они называются также координатно - параметрическими уравнениями прямой

Если прямая параллельна координатной оси то у направляющего вектора вторая координата равна нулю и уравнения (2) принимают вид:

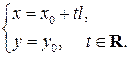
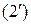
Поскольку то равенства 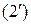означают, что у точек прямой первая координата может быть любым вещественным числом, в то время как вторая – фиксирована. Следовательно, точка 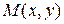лежит на прямой (рис. 3) тогда и только тогда, когда выполняется условие

(3)

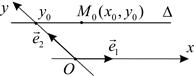
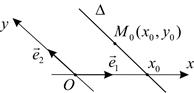
Рис. 3 Рис. 4

Аналогично, прямая проходящая через точку 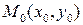и параллельна координатной оси 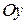(рис. 4), задается условием

(4)

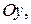Пусть прямая не параллельна координатным осям и т.е. 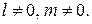В этом случае из системы (2) можно исключить и получить следующее уравнение прямой :

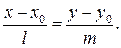(5)

Если (5) рассматривать как пропорцию, т.е. считать, что равенство (5) эквивалентно равенству 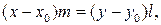то уравнениями вида (5) можно задавать все прямые без исключения, т.е. можно задавать и прямые, параллельные координатным осям. Например, уравнение означает, что т.е. (поскольку ). Таким образом, будем считать, что любая прямая может быть задана уравнением (5), которое называется каноническим уравнением прямой.

Если прямая не параллельна координатной оси 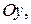т.е. то можно определить число которое называется угловым коэффициентом прямой. Название объясняется тем обстоятельством, что в случае прямоугольной системы координат 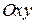на плоскости где 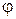– величина угла между осью и прямой (рис. 5).

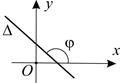
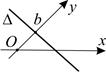
Рис. 5 Рис. 6

Разумеется, в случае общей декартовой системы координат, число не имеет такого геометрического смысла. Преобразовав уравнение (5), получаем следующее уравнение прямойпо точке 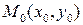и угловому коэффициенту :

(6)

В свою очередь, уравнение (6) очевидным образом приводится к виду

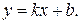(7)

Число здесь – величина отрезка, отсекаемого прямой на оси (рис. 6).

Любую прямую можно задать, указав две различные точки этой прямой и В таком случае – направляющий вектор этой прямой с координатами и 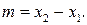Согласно (2) и (5), мы можем записать параметрические уравнения прямой по двум точкам:

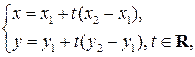(8)

а также каноническое уравнение прямой по двум точкам:

(9)

Отметим, что все приведенные выше непараметрические уравнения прямой (т.е. уравнения (3) – (7), (9)) являются линейными уравнениями вида В следующей теореме мы зафиксируем этот факт и покажем, что верно и обратное.

Теорема 2.3.1. Пусть 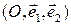– аффинный репер на плоскости .

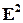(i) Любая прямая на плоскости 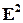может быть задана в данном репере линейным уравнением вида

(10)

(ii) Обратно, любое линейное уравнение (10) при условии, что числа и 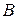не равны нулю одновременно, задает в данном репере прямую.

Доказательство. Истинность части (i) теоремы была отмечена перед ее формулировкой.

(ii) Пусть, для определенности, в уравнении (10). Тогда

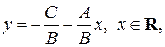
– общее решение уравнения (10). Поскольку 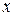может быть любым числом, обозначим 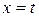и будем рассматривать в качестве параметра. Все решения уравнения (10) теперь можно записать в виде:

(11)

Сравнивая (11) с (2), можем сделать вывод, что уравнение (10) задает прямую с начальной точкой 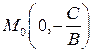и направляющим вектором Если в уравнении (10) то и доказательство проводится аналогично. 

Уравнение (10) называется общим уравнение прямой. В следующем утверждении описывается геометрический смысл коэффициентов общего уравнения прямой.

Утверждение 2.3.1. Пусть– общее уравнение прямой в репере 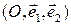. Тогда:

(i) вектор заданный своими координатами в базисе является направляющим вектором прямой

(ii) 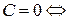прямая проходит через начало координат ();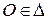

(iii) 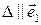(прямая параллельна оси либо совпадает с ней);

(iv) (прямая параллельна оси 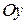либо совпадает с ней).

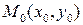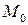Доказательство. (i) Пусть точка прямой Отложим от точки вектор получим точку Очевидно, что – направляющий вектор прямой тогда и только тогда, когда 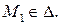Подставим координаты точки в уравнение (10). Получим:

Доказательство пунктов (ii) – (iv) предлагается провести читателю самостоятельно в качестве упражнения. 

Пусть в уравнении (10) прямой все коэффициенты ненулевые, т.е. прямая не параллельна координатным осям и не проходит через начало координат. Преобразуем последовательно уравнение (10):

~ ~ ~

Если ввести обозначения то получим уравнение прямой в следующем виде:

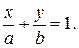(12)

Уравнение (12) называется уравнением прямой в отрезках, поскольку 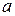и – величины отрезков, которые прямая отсекает на координатных осях (рис. 7).

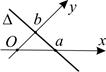
Рис. 7 Рис. 8

Будем называть нормальным вектором прямой любой вектор, перпендикулярный прямой. Пусть (10) – общее уравнение прямой в ортонормированном репере В этом случае вектор – нормальный вектор прямой Действительно, выше было отмечено, что вектор – направляющий вектор прямой, т.е. Так как то

Если для прямой заданы начальная точка 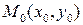своими координатами в ортонормированном репере 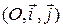и нормальный вектор прямой своими координатами в базисе то можно записать уравнение прямой в данном репере в виде:

(13)

В самом деле, очевидно, что точка 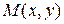лежит на прямой тогда и только тогда, когда векторы и 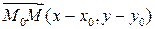перпендикулярны (рис. 8). Равенство (13) как раз и выражает это условие.

Следующая теорема показывает, как по общим уравнениям прямых можно определить тип их взаимного расположения.

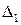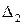Теорема 2.3.2. Пусть прямые и на плоскости 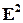заданы в некотором аффинном репере общими уравнениями:

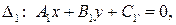
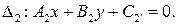
Тогда верны следующие утверждения:

(i) прямые 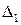и 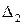совпадают тогда и только тогда, когда существует ненулевое число 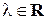такое, что (соответствующие коэффициенты уравнений прямых пропорциональны);

(ii) прямые 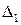и 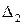параллельны тогда и только тогда, когда существует ненулевое число 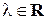такое, что но (соответствующие коэффициенты при неизвестных пропорциональны, однако их отношение не равно отношению свободных членов);

(iii) прямые 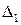и 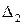пересекаются в одной точке тогда и только тогда, когда (коэффициенты при неизвестных не пропорциональны).

Доказательство. Заметим, что достаточно доказать справедливость любых двух из трех пунктов теоремы. Тогда третий пункт будет справедлив, поскольку это единственная возможная альтернатива двум другим.

Как было отмечено в утверждении 2.3.1, векторы и 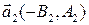– направляющие векторы соответственно прямых 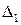и 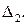Очевидно, что прямые совпадают или параллельны тогда и только тогда, когда их направляющие векторы коллинеарны, т.е. для некоторого ненулевого числа 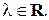Это означает, что выполняются равенства:

(14)

т.е. коэффициенты при неизвестных пропорциональны. При условии (14) рассмотрим систему уравнений

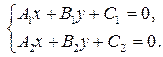(15)

Эта система задает пересечение прямых 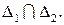Очевидно, что прямые параллельны тогда и только тогда, когда система (15) не имеет решений; прямые совпадают тогда и только тогда, когда система (15) имеет бесконечно много решений. Подставляя во второе уравнение 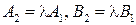и вычитая из него первое уравнение, умноженное на получим, что следствием системы (15) является условие Это условие приводит к противоречию (система (15) не имеет решений), если Следовательно, если прямые совпадают, то необходимо выполнение условий: 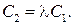Обратно, если соответствующие коэффициенты уравнений пропорциональны, то множества решений этих уравнений совпадают, т.е. Таким образом, доказана справедливость пунктов (i) и (ii) теоремы 2.3.1, а, следовательно, теорема полностью доказана. 

Дата добавления: 2014-01-07