
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Точки перегину
|
|
|
|
.
Знаходження екстремумів функцій
Означення 12.3. Будемо говорити, що в точці  функція
функція  має:
має:
а) локальний максимум 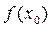 і позначати
і позначати 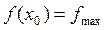 , якщо
, якщо
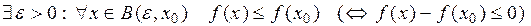 ;
;
б) строгий локальний максимум 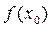 , і позначати
, і позначати 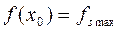 , якщо
, якщо
 ;
;
в) локальний мінімум 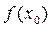 і позначати
і позначати 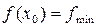 , якщо
, якщо
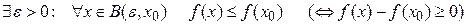 ;
;
г) строгий локальний мінімум 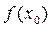 , і позначати
, і позначати  , якщо
, якщо
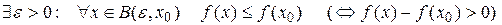 ;
;
д ) екстремум 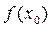 (приймає екстремальне значення), і позначати
(приймає екстремальне значення), і позначати
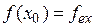 , якщо
, якщо  .
.
Теорема 12.7. (Необхідна умова екстремуму). Нехай функція  в точці
в точці 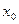
приймає екстремальне значення 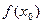 і в цій точці існує скінчена похідна
і в цій точці існує скінчена похідна 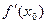 , тоді
, тоді
 . Тобто,
. Тобто, 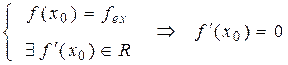 .
.
Доведення. Твердження теореми випливає з теореми Ферма. Дійсно, нехай, наприклад, 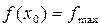 , тоді за означенням 12.3 знайдеться таке додатне число
, тоді за означенням 12.3 знайдеться таке додатне число 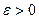 , що число
, що число 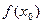 є найбільшим значенням функції
є найбільшим значенням функції  в інтервалі
в інтервалі  . Так як, за умовою теореми в точці
. Так як, за умовою теореми в точці 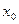 існує скінчена похідна
існує скінчена похідна 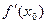 , то згідно теореми Ферма,
, то згідно теореми Ферма,  , що і потрібно було довести.
, що і потрібно було довести.
Означення 12.4. Будемо говорити, що проходячи через 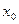
а) функція  змінює свій знак з “+” на “-”, і будемо позначати
змінює свій знак з “+” на “-”, і будемо позначати  , якщо
, якщо

б) функція  змінює свій знак з “-” на “+”, і будемо позначати
змінює свій знак з “-” на “+”, і будемо позначати 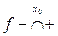 , якщо функція
, якщо функція 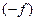 змінює свій знак з плюса на мінус.
змінює свій знак з плюса на мінус.
Теорема 12.8 (Про достатні умови екстремуму в термінах першої похідної). Якщо функція  має похідну в усіх точках інтервалу
має похідну в усіх точках інтервалу крім, можливо, однієї
крім, можливо, однієї 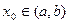 , в якій вона неперервна, і, проходячи через
, в якій вона неперервна, і, проходячи через 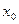 похідна функції
похідна функції  змінює свій знак, то тоді в цій точці функція
змінює свій знак, то тоді в цій точці функція  має екстремум. При цьому, функція
має екстремум. При цьому, функція  має у точці
має у точці 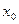 строгий локальний максимум, якщо похідна
строгий локальний максимум, якщо похідна 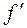 , проходячи через цю точку, змінює свій знак з плюса на мінус, і функція
, проходячи через цю точку, змінює свій знак з плюса на мінус, і функція  має у точці
має у точці 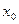 строгий локальний мінімум - у протилежному випадку. Тобто,
строгий локальний мінімум - у протилежному випадку. Тобто,
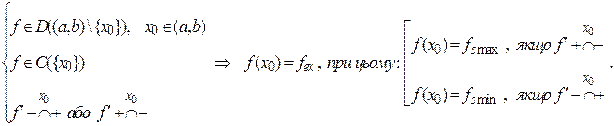
Доведення. Нехай функція  неперервна в точці
неперервна в точці 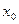 , і при цьому похідна
, і при цьому похідна 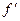 , проходячи через точку
, проходячи через точку 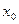 змінює, наприклад, свій знак з “+” на “-”. Тоді з теореми 12.3 випливає, що при деякому
змінює, наприклад, свій знак з “+” на “-”. Тоді з теореми 12.3 випливає, що при деякому 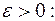
|
|
|
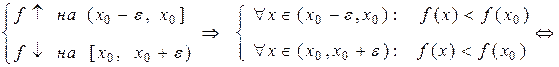

Аналогічно доводиться випадок строгого мінімуму. (Перевірити самостійно!!!). Теорему доведено.
Зауваження 12.4. Якщо в умовах попередньої теореми існує похідна 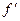 , то за теоремою 12.7 ця похідна дорівнює нулю. Точки, в яких похідна функції
, то за теоремою 12.7 ця похідна дорівнює нулю. Точки, в яких похідна функції  рівна нулю називають ще стаціонарними або критичними.
рівна нулю називають ще стаціонарними або критичними.
Теорема 12.9 (Про достатні умови екстремуму в термінах вищих похідних).
Нехай в деякій точці 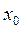 інтервалу
інтервалу  , на якому означена функція
, на якому означена функція  і має всі похідні до (n-1) – го порядку включно, функція
і має всі похідні до (n-1) – го порядку включно, функція  має відмінну від нуля похідну ще і n – го порядку, причому всі похідні меншого порядку у цій точці
має відмінну від нуля похідну ще і n – го порядку, причому всі похідні меншого порядку у цій точці 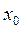 дорівнюють нулю. Тоді, якщо число n – парне, то в точці
дорівнюють нулю. Тоді, якщо число n – парне, то в точці 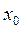 функція
функція  має екстремум, при цьому цей екстремум є локальним максимумом, коли n-та похідна від’ємна, і цей екстремум є локальним мінімумом, коли – додатна. Якщо ж число n – непарне, то в точці
має екстремум, при цьому цей екстремум є локальним максимумом, коли n-та похідна від’ємна, і цей екстремум є локальним мінімумом, коли – додатна. Якщо ж число n – непарне, то в точці 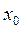 функція
функція  не має екстремуму.
не має екстремуму.
Доведення. Нехай функція  означена і має всі похідні до (n-1)-го порядку включно на деякому інтервалі
означена і має всі похідні до (n-1)-го порядку включно на деякому інтервалі  і n-ту похідну в точці
і n-ту похідну в точці 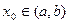 . Тоді за теоремою Пеано про формулу Тейлора (теорема 11.3) справджується рівність (11.5):
. Тоді за теоремою Пеано про формулу Тейлора (теорема 11.3) справджується рівність (11.5):

Але за умовою теореми 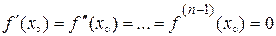 . Тому,
. Тому,
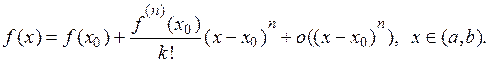 Звідки маємо:
Звідки маємо:
 (12.1).
(12.1).
За означенням нескінченно малої величини більшого порядку  , тому, знайдеться таке число
, тому, знайдеться таке число 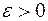 , що
, що 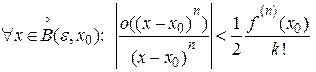 .
.
Звідки слідує, що знаки числа 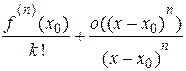 і числа
і числа 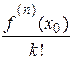 однакові. Таким чином, і знак добутку, що стоїть у правій частині рівності (12.1), а разом з цим і різниці
однакові. Таким чином, і знак добутку, що стоїть у правій частині рівності (12.1), а разом з цим і різниці 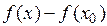 , співпадає зі знаком числа
, співпадає зі знаком числа 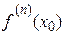 , якщо число
, якщо число 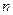 - парне, і, тому, множник
- парне, і, тому, множник 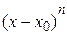 - додатний. Отже, справджується перше твердження теореми.
- додатний. Отже, справджується перше твердження теореми.
Якщо ж число 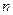 - непарне, то для довільного числа
- непарне, то для довільного числа 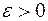 множник
множник 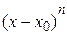 - додатний, коли
- додатний, коли 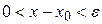 , і множник
, і множник 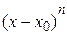 - від’ємний,, коли
- від’ємний,, коли 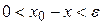 .
.
Отже, у 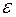 - околі точки
- околі точки 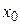 приріст
приріст 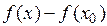 приймає значення різних знаків. Таким чином, у цьому випадку функція
приймає значення різних знаків. Таким чином, у цьому випадку функція  не має екстремуму в точці
не має екстремуму в точці 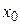 .
.
Теорему доведено.
Означення 12.5. Будемо говорити, що точка  є точкою перегину графіка функції
є точкою перегину графіка функції  , і позначати
, і позначати 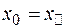 для
для  , якщо:
, якщо:
|
|
|
 ,
,
тобто, функція  має різні напрямки строгої опуклості зліва і справа від точки
має різні напрямки строгої опуклості зліва і справа від точки 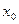 , і є неперервною в цій точці.
, і є неперервною в цій точці.
Теорема 12.10. (Необхідна умова точки перегину ). Нехай точка  є точкою перегину графіка функції
є точкою перегину графіка функції  , і в цій точці функція
, і в цій точці функція  має другу похідну. Тоді ця похідна дорівнює нулю. Тобто,
має другу похідну. Тоді ця похідна дорівнює нулю. Тобто,
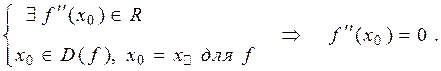
Доведення. За означенням 12.5 точки перегину графіка функції  та за теоремою 12.8 випливає, що в точці перегину
та за теоремою 12.8 випливає, що в точці перегину 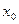 похідна
похідна 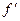 функції
функції  приймає своє екстремальне значення, тобто
приймає своє екстремальне значення, тобто  . Так як в цій точці існує друга похідна
. Так як в цій точці існує друга похідна  , то та за теоремою 12.7 про необхідну умову екстремуму ця похідна дорівнює нулю. Що і потрібно було довести.
, то та за теоремою 12.7 про необхідну умову екстремуму ця похідна дорівнює нулю. Що і потрібно було довести.
Теорема 12.11. (Про достатні умови існування точки перегину графіка функції ). Якщо функція  має другу похідну в усіх точках інтервалу
має другу похідну в усіх точках інтервалу крім, можливо, однієї
крім, можливо, однієї 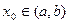 , в якій вона неперервна, і, проходячи через цю точку
, в якій вона неперервна, і, проходячи через цю точку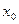 друга похідна функції
друга похідна функції  змінює свій знак, то тоді точка
змінює свій знак, то тоді точка 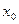 є точкою перегину графіка функції
є точкою перегину графіка функції  .
.
Доведення. Якщодруга похідна функції  змінює свій знак, проходячи через точку
змінює свій знак, проходячи через точку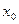 , то за теоремою 12.6 слідує, що cправа і зліва від цієї точки функція
, то за теоремою 12.6 слідує, що cправа і зліва від цієї точки функція  має різну направленість опуклості, тобто, згідно означення 12.5, точка
має різну направленість опуклості, тобто, згідно означення 12.5, точка 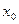 є точкою перегину графіка функції
є точкою перегину графіка функції  . Теорему доведено.
. Теорему доведено.
Рекомендована схема дослідження функції і побудови її графіка
1. Знаходження області визначення функції.
2. Визначення періодичності, парності і непарності, точок перетину графіка функції з координатними осями.
3. Дослідження функції методами теорії границь: знаходження області неперервності функції, точок розриву і визначення їх типу розриву, знаходження асимптот графіка функції.
4. Дослідження функції за допомогою першої похідної: знаходження похідної, побудова схеми розподілу її знаків, визначення інтервалів монотонності функції та точок екстремумів.
5. Дослідження функції за допомогою другої похідної: знаходження другої похідної, побудова схеми розподілу її знаків, визначення інтервалів опуклості функції та точок перегину графіка функції.
6. Зведення результатів дослідження в єдину таблицю.
7. Побудова за таблицею результатів дослідження функції її графіка.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 971; Нарушение авторских прав?; Мы поможем в написании вашей работы!