Завдання для самостійної роботи 6.3: Довести необхідністьтеореми 6.4

Домовленість: В попередньому означенні і надалі, якщо не сказано противне, для спрощення будемо вважати, що область визначення функцій містять деякий, хоч би виколотий, окіл граничної точки. Інакше, відповідні зміни в означені і твердженнях – очевидні.

Теорема 6.5 (Про умови існування границі функції в термінах односторонніх границь). Нехай,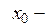гранична точка множини .

Тоді число є границею функції в точці тоді і тільки тоді, коли існують ліва і права односторонні границі функції в цій точці, співпадають між собою і рівні числу 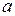. Тобто,

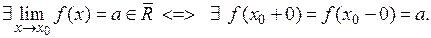
Доведення. Твердження теореми випливає з того, що для довільної точки і числа 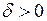справджується рівність Тому достатність теореми доводиться так: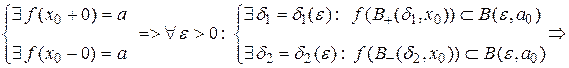

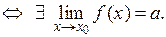
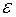Тобто, якщо існують односторонні границі, які рівні числу , то для довільного- околу цього числа знайдуться лівий та правий околи граничної точки відповідних діаметрів та , які відображаються у 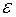-окіл точки . Звідки слідує, що об’єднання цих околів з діаметрами , яке виколотим -околом граничної точки, теж відображається у 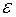-окіл точки . Тому число 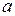є границею функції у точці 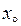, що і потрібно було довести.

Наслідок 6.1 (Необхідні і достатні умови неперервності функції в термінах односторонніх границь). Функція неперервна в точці тоді і тільки тоді, коли існують в точці 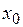границі функції зліва і з права, співпадають між собою і рівні значеню функції у цій точці. Тобто:

(6.4).

Означення 6.4. Якщо функція означення в деякому околі точки і порушуються умови існування або рівності (6.4), то точку 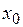називають точкою розриву функції . При цьому, якщо існують і є скінченими границі , але порушуються рівності (6.4), то кажуть що функція в точці 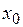має розрив першого типу (роду). А якщо хоч одна з двох границь не існує або не є скінченою, то кажуть, що ф-ція має в точці 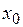розрив другого типу (роду). В свою чергу, у випадку розриву першого роду, якщо порушується перша з рівностей (6,4), тобто, 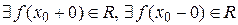але то кажуть що в точці розриву 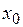ф-ція має (здійснює) стрибок величини 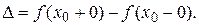А якщо порушується друга рівність (7,2), тобто

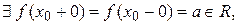але або 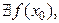то кажуть, що 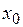є точкою усувного розриву (в цьому випадку, якщо переозначити ф-цію в точці 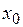, поклавши 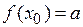, то ф-ція стає неперервною в цій точці).

Означення 6.5. Функція називається неперервною зправа в точці , якщо 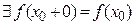, і - неперервною зліва, якщо 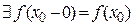. Функція називається неперервною на відрізку 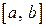, якщо вона неперервна у кожній точці інтервалу і є неперервною справа у точці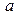та є неперервною зліва у точці .

Зауваження 6.3. Для односторонніх границь та односторонньої неперервності функції виконуються ті ж самі теореми що і для звичайних (повних) границь та неперервності. Щоб показати це, досить у відповідних теоремах повні околи граничної точки замінити на односторонні.

Дата добавления: 2014-01-07