
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема 7.1 ( Про неперервність основних елементарних функцій )
|
|
|
|
.
Неперервність основних елементарних функцій.
Лекція № 7.
Приклад 7.1. Розглянемо функцію  . Виберемо довільні числа
. Виберемо довільні числа 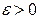 та
та  . Тоді за нерівністю
. Тоді за нерівністю  слідує нерівність
слідує нерівність
Отже, має місце рівність  , тобто, функція
, тобто, функція  є неперервною у будь-якій точці
є неперервною у будь-якій точці  числової осі.
числової осі.
Тоді за теоремою про збереження неперервності функцій при арифметичних операціях над ними (теорема 6.1) функція  теж є неперервною у будь-якій точці
теж є неперервною у будь-якій точці  при довільному натуральному показнику степеня
при довільному натуральному показнику степеня  .
.
Аналогічно, за тією ж теоремою функція 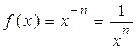 є неперервною на всій дійсній числовій осі крім точки
є неперервною на всій дійсній числовій осі крім точки  .
.
Так як функція  ,
,  , є строго зростаючою і неперервною на
, є строго зростаючою і неперервною на  , то обернена до неї функція
, то обернена до неї функція  теж є неперервною (за теоремою про неперервність оберненої функції).
теж є неперервною (за теоремою про неперервність оберненої функції).
Аналогічно, функція 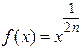 ,
,  , є неперервною на пів осі
, є неперервною на пів осі  .
.
Тоді, знову ж таки за теоремою про збереження неперервності функцій при арифметичних операціях над ними, функції 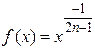 та
та 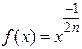 ,
,  , є неперервними у кожній точці їх областей визначення.
, є неперервними у кожній точці їх областей визначення.
Наслідок 7.1. Степенева функція  є неперервною у кожній точці її області визначення при будь-якому раціональному показнику степеня
є неперервною у кожній точці її області визначення при будь-якому раціональному показнику степеня 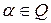 .
.
Всі основні елементарні функції, тобто функції 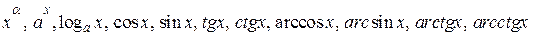
є неперервними у кожній точці їх областей визначення.
Доведення: 1) Доведемо, спочатку, що показникові функція  , є неперервною у нулі.
, є неперервною у нулі.
Для цього покажемо, що 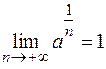 (7.1).
(7.1).
Нехай  Тоді знайдеться таке натуральне число
Тоді знайдеться таке натуральне число 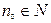 , що дла всіх більших за
, що дла всіх більших за  чисел
чисел  виконуються нерівності
виконуються нерівності 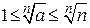 . Але,
. Але,  , тому, за теоремою про три послідовності,
, тому, за теоремою про три послідовності,  ,
, 
Якщо 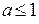 , то
, то  , так як
, так як  . Таким чином, рівність (7.1) доведено для всіх
. Таким чином, рівність (7.1) доведено для всіх 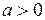 .
.
Виберемо довільну послідовність  додатних чисел, яка збігається до нуля:
додатних чисел, яка збігається до нуля:  і
і  Покладемо
Покладемо  де
де 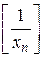 - ціла частина числа
- ціла частина числа  . Тоді,
. Тоді, 
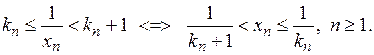 Тому виконуються нерівності
Тому виконуються нерівності  , якщо
, якщо 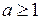 , і
, і  , якщо
, якщо 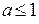 . Але послідовності чисел
. Але послідовності чисел 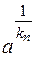 та
та  є під послідовностями послідовності
є під послідовностями послідовності  , яка збігається до одиниці при
, яка збігається до одиниці при  . Тому,
. Тому,  . А значить, за теоремою про три послідовності, маємо
. А значить, за теоремою про три послідовності, маємо  Отже, згідно означення границі функції за Гейне,
Отже, згідно означення границі функції за Гейне,  , тобто, показникова функція
, тобто, показникова функція 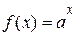 є неперервною у нулі зправа. Але,
є неперервною у нулі зправа. Але, 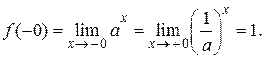 Таким чином, функція неперервна з обох сторін в точці
Таким чином, функція неперервна з обох сторін в точці  , тому, показникова функція
, тому, показникова функція 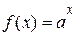 є неперервною у нулі.
є неперервною у нулі.
|
|
|
Нехай точка 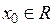 - довільна. Позначимо
- довільна. Позначимо 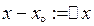 , тоді маємо
, тоді маємо
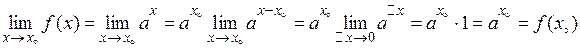 . Отже, показникова функція
. Отже, показникова функція 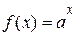 є неперервною на всій числовій осі.
є неперервною на всій числовій осі.
2) Нехай  . Так як логарифмічна функція є оберненою до показникової, неперервної і строго монотонної, то неперервність логарифмічної функції випливає з теореми про неперервність оберненої функції (теорема 6.12).
. Так як логарифмічна функція є оберненою до показникової, неперервної і строго монотонної, то неперервність логарифмічної функції випливає з теореми про неперервність оберненої функції (теорема 6.12).
3) Нехай 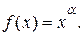 Якщо показник степеня
Якщо показник степеня 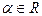 - раціональний, то неперервність функції була доведена раніше (приклад 7.1).Якщо
- раціональний, то неперервність функції була доведена раніше (приклад 7.1).Якщо  - ірраціональне число, то
- ірраціональне число, то
 Тому, в цьому випадку, неперервність степеневої функції випливає з теореми про збереження неперервності функцій при арифметичних операціях над ними (теорема 6.1) та про неперервність складної функції (теорема 6.3).
Тому, в цьому випадку, неперервність степеневої функції випливає з теореми про збереження неперервності функцій при арифметичних операціях над ними (теорема 6.1) та про неперервність складної функції (теорема 6.3).
4) Доведемо неперервність функції 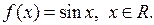
Дійсно,
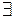

=
Тому, за означенням границі по Коші,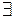
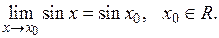
Отже, функція  неперервна на множині дійсних чисел
неперервна на множині дійсних чисел  .
.
5) Неперервність функції  випливає з неперервності функцій
випливає з неперервності функцій  та
та 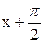 , так як
, так як 
6) Неперервність функцій 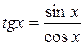 і
і  на відповідних областях їх визначення слідує за теоремою про збереження неперервності функцій при арифметичних операціях над ними (теорема 6.1).
на відповідних областях їх визначення слідує за теоремою про збереження неперервності функцій при арифметичних операціях над ними (теорема 6.1).
7) Неперервність функцій  і
і 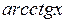 на їх областях визначення слідує за теоремами про неперервність оберненої функції (теореми 6.11-6.12) і вище доведеного.
на їх областях визначення слідує за теоремами про неперервність оберненої функції (теореми 6.11-6.12) і вище доведеного.
Доведення теореми закінчено.
Перейдемо до доведення теореми про класичні границі функцій у точці нуль.
Доведення теореми 5.10. І.1) Границю 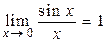 було доведено в теоремі 5.7.
було доведено в теоремі 5.7.
2) Так як функція  неперервна в точці нуль і має границю
неперервна в точці нуль і має границю  , то за теоремою про збереження арифметичних операцій при взятті границі функції (теорема 5.4) маємо:
, то за теоремою про збереження арифметичних операцій при взятті границі функції (теорема 5.4) маємо: 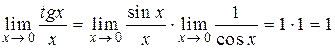 .
.
|
|
|
3) Функція 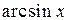 неперервна, і,тому, має границю в нулі, а також існує границя функції
неперервна, і,тому, має границю в нулі, а також існує границя функції  , і, таким чином, функцію
, і, таким чином, функцію  можна вважати неперервною у нулі, якщо доозначити її у цій точці одиницею. Отже, згідно теореми 6.2 про границю складної функції, маємо
можна вважати неперервною у нулі, якщо доозначити її у цій точці одиницею. Отже, згідно теореми 6.2 про границю складної функції, маємо  .
.
4) Аналогічно,  (Довести самостійно!!!).
(Довести самостійно!!!).
5) Точно так, згідно теореми 6.2 про границю складної функції та теореми про збереження арифметичних операцій при взятті границі функції (т еорема 5.4) маємо:
 .
.
6) Аналогічно, 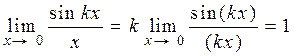 .
.
ІІ. 1) Нехай  . Покладемо
. Покладемо  . Тоді
. Тоді 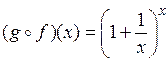 . У теоремі 5.8 було доведено, що
. У теоремі 5.8 було доведено, що  . Отже, якщо доозначити функцію
. Отже, якщо доозначити функцію 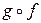 у точці
у точці  як
як  , то функція стає неперервною у цій точці. Функція
, то функція стає неперервною у цій точці. Функція  має неперервну обернену, і
має неперервну обернену, і  . Тому, згідно теореми 6.4, виконавши заміну змінної
. Тому, згідно теореми 6.4, виконавши заміну змінної 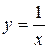 , отримаємо:
, отримаємо: 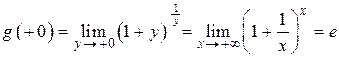 .
.
Аналогічно,  .
.
Так як існують границі 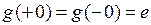 , то, згідно теореми 6.5, існує границя
, то, згідно теореми 6.5, існує границя
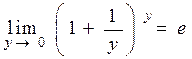 .
.
2) Так як функція  є неперервною і існує границя
є неперервною і існує границя  то згідно теореми про границю складної функції (теорема 6.2), існує границя
то згідно теореми про границю складної функції (теорема 6.2), існує границя  .
.
3) Відповідно, при 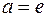 маємо:
маємо:  .
.
4) Так як функція  є неперервною і монотонною, то вона має неперервну обернену функцію
є неперервною і монотонною, то вона має неперервну обернену функцію 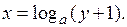 Отже, згідно тереми 6.4, можна виконати заміну
Отже, згідно тереми 6.4, можна виконати заміну  , маємо:
, маємо:
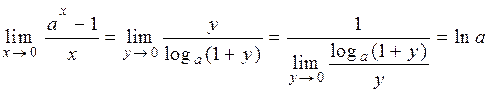 .
.
5) Відповідно, якщо 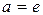 , то
, то 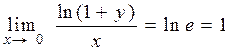 .
.
6) Аналогічно, функція  є строго монотонною і неперервною в лівому і правому околі точки
є строго монотонною і неперервною в лівому і правому околі точки  Отже, користуючись аргументацією попереднього пункту, і виконавши заміну
Отже, користуючись аргументацією попереднього пункту, і виконавши заміну  , та враховуючи співвідношення
, та враховуючи співвідношення 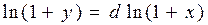 , маємо
, маємо 
Теорему доведено.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2608; Нарушение авторских прав?; Мы поможем в написании вашей работы!