
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторное произведение векторов
Определение 1.6.1. Пусть 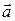 и
и  – неколлинеарные векторы. Векторным произведением вектора
– неколлинеарные векторы. Векторным произведением вектора 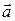 на вектор
на вектор  называется вектор, который обозначается
называется вектор, который обозначается  и определяется следующими условиями:
и определяется следующими условиями:
(i) 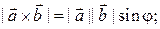
(ii) 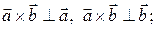
(iii) упорядоченная тройка векторов 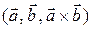 – правая.
– правая.
Если 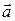 и
и  – коллинеарные векторы, то их векторное произведение полагают равным нулевому вектору:
– коллинеарные векторы, то их векторное произведение полагают равным нулевому вектору: 
В случае неколлинеарных векторов условие (i) определяет только длину (ненулевую) вектора  . Условиям (i) и (ii), очевидно, удовлетворяют два взаимно противоположных вектора. И только все три условия (i), (ii), (iii) задают вектор
. Условиям (i) и (ii), очевидно, удовлетворяют два взаимно противоположных вектора. И только все три условия (i), (ii), (iii) задают вектор  однозначно (рис. 6.1).
однозначно (рис. 6.1).
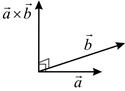

Рис. 6.1 Рис. 6.2
Отметим, что для неколлинеарных векторов длина 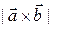 векторного произведения численно равна площади параллелограмма, построенного на векторах
векторного произведения численно равна площади параллелограмма, построенного на векторах 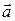 и
и  (рис. 6.2).
(рис. 6.2).
Рассмотрим геометрическую конструкцию, позволяющую строить векторное произведение  векторов, первый из которых имеет единичную длину,
векторов, первый из которых имеет единичную длину, 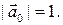 Пусть
Пусть 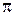 – плоскость, перпендикулярная вектору
– плоскость, перпендикулярная вектору 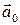 (рис. 6.3). Отложим векторы
(рис. 6.3). Отложим векторы 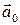 и
и  от точки
от точки 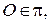 получим соответственно точки
получим соответственно точки  и
и 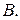 Пусть
Пусть 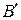 – ортогональная проекция точки
– ортогональная проекция точки 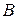 на плоскость
на плоскость 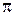 . Если векторы
. Если векторы 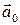 и
и  коллинеарны, то
коллинеарны, то 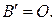 Если векторы
Если векторы 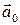 и
и  не коллинеарны, то
не коллинеарны, то 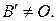 Повернем отрезок
Повернем отрезок 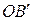 вокруг точки
вокруг точки 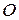 на угол
на угол 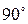 в направлении, противоположном движению часовой стрелки, если смотреть на плоскость
в направлении, противоположном движению часовой стрелки, если смотреть на плоскость 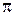 из точки
из точки  Получим отрезок
Получим отрезок 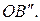 В случае коллинеарности
В случае коллинеарности 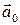 и
и  отрезок
отрезок 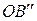 – нулевой, следовательно,
– нулевой, следовательно, 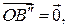 т.е. вектор
т.е. вектор 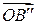 совпадает с вектором
совпадает с вектором 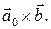 Убедимся, что
Убедимся, что 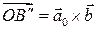 и в случае, когда векторы
и в случае, когда векторы 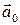 и
и  не коллинеарны (
не коллинеарны (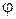 – величина угла между
– величина угла между 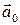 и
и 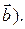 Проверяем условия (i),(ii),(iii) определения 6.1:
Проверяем условия (i),(ii),(iii) определения 6.1:
(i) 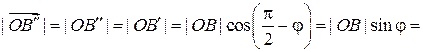
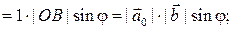
(ii) 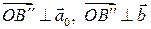 (по построению);
(по построению);
(iii) тройка 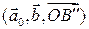 – правая (по построению).
– правая (по построению).
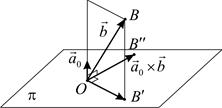
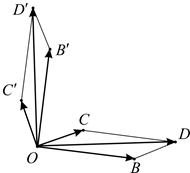
Рис. 6.3 Рис. 6.4
Таким образом, векторное произведение  единичного вектора
единичного вектора 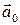 на вектор
на вектор  получается последовательным выполнением двух операций: ортогональной проекции
получается последовательным выполнением двух операций: ортогональной проекции  вектора
вектора  на плоскость
на плоскость 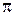 (получаем вектор
(получаем вектор 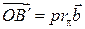 ) и последующим поворотом
) и последующим поворотом 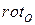 на угол
на угол 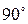 полученного вектора в плоскости
полученного вектора в плоскости 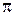 вокруг точки
вокруг точки 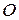 (получаем вектор
(получаем вектор 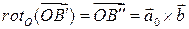 ).
).
Ранее отмечалось (см. § 1.3), что проектирование является линейным оператором, в частности, проектирование перестановочно с операцией сложения векторов:

Аналогичным свойством обладает и поворот векторов плоскости вокруг фиксированной точки на угол 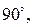 т.е.
т.е.
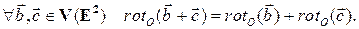 [1]
[1]
Убедимся в справедливости последнего равенства в случае, когда векторы  и
и 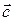 неколлинеарны. В этом случае сумму
неколлинеарны. В этом случае сумму 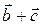 можно найти по правилу параллелограмма:
можно найти по правилу параллелограмма: 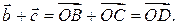 (рис. 6.4). Повернем параллелограмм
(рис. 6.4). Повернем параллелограмм 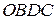 как целое вокруг точки
как целое вокруг точки 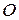 на угол
на угол 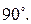 При этом векторы
При этом векторы 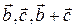 также повернутся на угол
также повернутся на угол 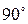 и перейдут соответственно в векторы
и перейдут соответственно в векторы 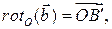
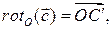
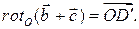 Так как после поворота параллелограмм останется параллелограммом, то
Так как после поворота параллелограмм останется параллелограммом, то 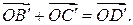 Это и означает справедливость доказываемого равенства. Похожим образом рассматривается случай коллинеарных векторов.
Это и означает справедливость доказываемого равенства. Похожим образом рассматривается случай коллинеарных векторов.
Сказанное выше позволяет утверждать, что для любого единичного вектора 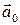 и любых векторов
и любых векторов  и
и 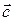 справедливо равенство:
справедливо равенство:
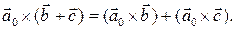 (1)
(1)
Установим теперь основные свойства векторного произведения.
Утверждение 1.6.1. Для любых векторов  и любого числа
и любого числа  верны следующие равенства:
верны следующие равенства:
(i) 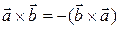 – свойство антикоммутативности векторного произведения;
– свойство антикоммутативности векторного произведения;
(ii) 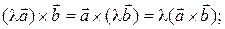
(iii) 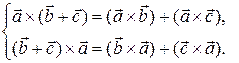
Справедливость равенств (ii) и (iii) означает, что векторное произведение (как и скалярное) билинейно.
(iv) 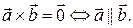
Свойство (iv) означает, что равенство нулю векторного произведения двух векторов является критерием их коллинеарности.
Доказательство. (i) По определению, в случае коллинеарных векторов 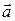 и
и  имеем:
имеем: 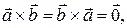 следовательно, доказываемое равенство верно. Если
следовательно, доказываемое равенство верно. Если 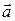 и
и  – неколлинеарные векторы, то для векторов
– неколлинеарные векторы, то для векторов  и
и  условия (i) и (ii) определения 1.6.1 совпадают, следовательно, векторы
условия (i) и (ii) определения 1.6.1 совпадают, следовательно, векторы  и
и  либо совпадают, либо противоположны. Рассмотрим правую тройку
либо совпадают, либо противоположны. Рассмотрим правую тройку 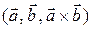 . Тройку
. Тройку 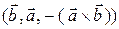 можно получить из данной, применяя последовательно две операции: вначале переставляя первые два элемента, а затем меняя третий вектор на противоположный. Поскольку каждая из этих операций меняет ориентацию на противоположную (см. § 1.4), то тройка
можно получить из данной, применяя последовательно две операции: вначале переставляя первые два элемента, а затем меняя третий вектор на противоположный. Поскольку каждая из этих операций меняет ориентацию на противоположную (см. § 1.4), то тройка 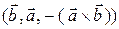 – правая. Следовательно,
– правая. Следовательно, 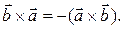
(ii) Если векторы 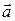 и
и  коллинеарны или
коллинеарны или  то векторы
то векторы 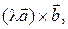
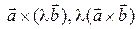 – нулевые, следовательно, они совпадают. Пусть
– нулевые, следовательно, они совпадают. Пусть 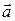 и
и  не коллинеарны и
не коллинеарны и 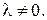 Тогда каждый из векторов
Тогда каждый из векторов 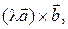
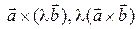 имеет длину, равную
имеет длину, равную  и сонаправлен с вектором
и сонаправлен с вектором  при
при  и противоположно направлен с вектором
и противоположно направлен с вектором  , если
, если 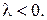 Следовательно,
Следовательно, 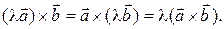
(iii) Докажем справедливость для любых векторов первого равенства:
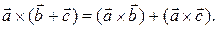 (2)
(2)
Второе равенство, очевидно, следует из первого, если воспользоваться уже доказанной антикоммутативностью векторного произведения.
Если  то доказываемое равенство справедливо, поскольку в обеих его частях стоят нулевые векторы. Пусть
то доказываемое равенство справедливо, поскольку в обеих его частях стоят нулевые векторы. Пусть 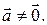 Нормируем вектор
Нормируем вектор 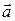 , т.е. рассмотрим вектор
, т.е. рассмотрим вектор  Выше было отмечено (см. равенство (1)), что для любых векторов
Выше было отмечено (см. равенство (1)), что для любых векторов 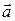 и
и  верно равенство:
верно равенство:
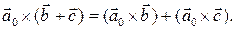
Для завершения доказательства умножим левую и правую части последнего равенства на число 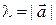 и воспользуемся уже доказанным свойством (ii).
и воспользуемся уже доказанным свойством (ii).
Свойство (iv) следует непосредственно из определения векторного произведения.
Найдем выражение векторного произведения через координаты векторов. Пусть векторы 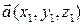 и
и 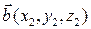 заданы своими координатами в некотором правом ортонормированном базисе
заданы своими координатами в некотором правом ортонормированном базисе 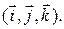 Пользуясь билинейностью векторного произведения, получаем:
Пользуясь билинейностью векторного произведения, получаем:
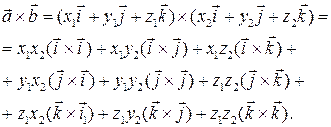 (3)
(3)
Произведения базисных векторов вычисляем по определению векторного произведения:

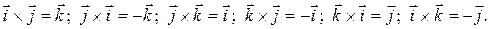
Таким образом, таблица умножения (векторного) базисных векторов имеет вид:
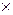
| 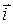
| 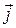
| 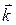
|
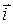
| 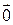
| 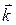
| 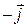
|
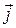
| 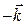
| 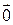
| 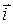
|
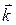
| 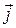
| 
| 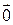
|
Возвращаясь к (3), получаем:

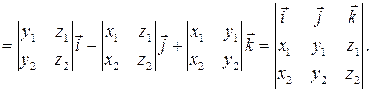
Окончательно, зафиксируем следующую формулу для вычисления векторного произведения векторов:
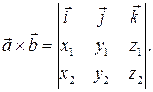 (4)
(4)
Поскольку два вектора 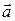 и
и  всегда компланарны, то их можно считать векторами некоторой плоскости
всегда компланарны, то их можно считать векторами некоторой плоскости 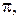 т.е.
т.е. 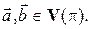 В таком случае векторы можно задать координатами в ортонормированном базисе
В таком случае векторы можно задать координатами в ортонормированном базисе 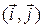 множества
множества 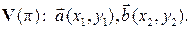 Определив вектор
Определив вектор 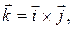 получим, очевидно, правый ортонормированный базис
получим, очевидно, правый ортонормированный базис 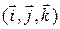 множества векторов пространства
множества векторов пространства  Так как
Так как
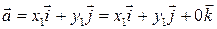 и
и 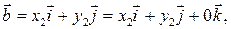
то в базисе 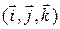 векторы
векторы 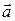 и
и  будут иметь следующие координаты:
будут иметь следующие координаты: 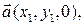
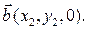 Согласно (4), их векторное произведение равно:
Согласно (4), их векторное произведение равно:
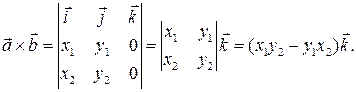
Из полученной формулы вытекает справедливость следующего утверждения.
Утверждение 1.6.2. Пусть векторы плоскости 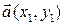 и
и 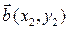 заданы своими координатами в ортонормированном базисе. Тогда:
заданы своими координатами в ортонормированном базисе. Тогда:
(i) 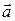 и
и  коллинеарны тогда и только тогда, когда
коллинеарны тогда и только тогда, когда 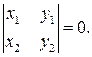
(ii) если векторы 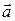 и
и  не коллинеарны, то площадь параллелограмма, построенного на векторах
не коллинеарны, то площадь параллелограмма, построенного на векторах 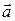 и
и  , равна
, равна 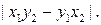
Операцию векторного произведения векторов можно рассматривать как отображение
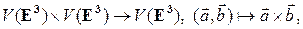
т.е. как бинарную алгебраическую операцию[2] в множестве всех векторов. Ранее отмечалось, что эта операция билинейна и антикоммутативна (утверждение 1.6.1). Отметим, что векторное произведение (в отличие от операции сложения векторов) не ассоциативно, т.е. равенство 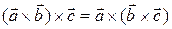 неверно для любых векторов
неверно для любых векторов 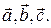 Например, для векторов правого ортонормированного базиса
Например, для векторов правого ортонормированного базиса 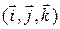 имеем:
имеем: 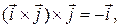 однако
однако 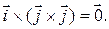 Тем не менее, для векторного произведения свойство ассоциативности имеет альтернативу.
Тем не менее, для векторного произведения свойство ассоциативности имеет альтернативу.
Утверждение 1.6.3. Для любых векторов  верно следующее равенство, которое называется тождеством Якоби:
верно следующее равенство, которое называется тождеством Якоби:
 (5)
(5)
Доказательство. Очевидно, что для любых векторов  в пространстве можно выбрать такой правый ортонормированный базис
в пространстве можно выбрать такой правый ортонормированный базис 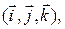 в котором векторы будут иметь следующие координаты:
в котором векторы будут иметь следующие координаты: 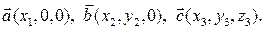 Тогда, применяя несколько раз формулу (4), получим:
Тогда, применяя несколько раз формулу (4), получим:
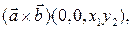

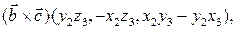
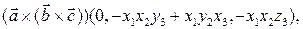
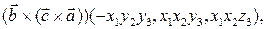
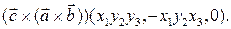
Легко проверить, что сумма последних трех векторов равна 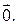
|
Дата добавления: 2014-01-07; Просмотров: 869; Нарушение авторских прав?; Мы поможем в написании вашей работы!