Теорема 10.3 ( Лагранжа про середнє значення, або про скінчений приріст )

.

Тобто, якщо функція неперервна на відрізку 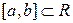і має похідну в усіх його внутрішніх точках, то знайдеться така точка з інтервалу , що приріст функції на відрізку буде рівний добутку похідної функції в цій точці на приріст аргумента.

Доведення. Розглянемо функцію

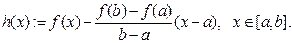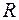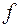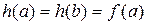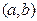Так як другий доданок, що є лінійною функцією, неперервний і має похідну на всій множині дійсних чисел , то з умов, накладених на функцію , випливає, що функція є неперервною на відрізку і має похідну в його внутрішніх точках, тобто, і . До того ж, . Таким чином, функція задовольняє умовам теореми Ролля і, отже, знайдеться така точка із інтервалу , в якій похідна цієї функції дорівнює нулю. Тобто,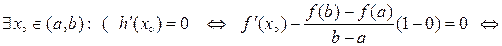

що і потрібно було довести.

Наслідок 10.1. 1) Якщо в усіх точках інтервалу функція 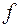має похідну 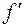рівну нулю, то функція є постійною на цьому інтервалі. Тобто,

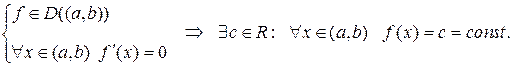
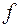2) якщо в усіх точках інтервалу існують і співпадають похідні двох функцій і 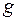, то ці функції можуть різнитися тільки на постійну величину. Тобто,

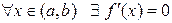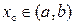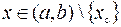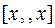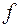Доведення. 1) Нехай . Виберемо довільне . Тоді для будь якого на відрізку або, відповідно, на функція задовольняє умовам теореми Лагранжа, а, значить,

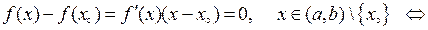
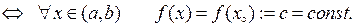
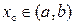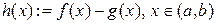За довільністю вибору точки слідує справедливість першого твердження. 2) Нехай . Розглянемо функцію . Очевидно, 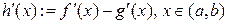. Отже, згідно попереднього пункту наслідку, 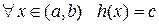. Тобто,.

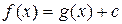Наслідок доведено.

Зауваження10.1. Теорема Лагранжа є узагальненням теореми Ролля і має таке геометричне тлумачення: якщо виконуються умови теореми, то на графіку функції знайдеться така точка, в якій дотична паралельна хорді, що сполучає кінці графіка.

Теорема 10.4 (Коші про відношення приростів двох функцій). Якщо функці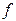ї і 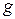є неперервними на відрізку , у внутрішніх точках якого вони мають скінчену похідну, причому похідна функції відмінна від нуля, то знайдеться така внутрішня точка відрізка, у якій відношення приросту функції 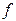до приросту функції 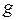на відрізку буде рівне відношенню похідних відповідних функцій у цій точці. Тобто,

Доведення. За умовою випливає, що 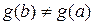. Інакше, згідно теореми Ролля, для функції 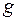знайшлася б точка , що суперечить умові теореми. Побудуємо функцію

.

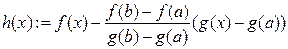Неважко переконатись, що тобто, для функції виконується умова теореми Ролля. Тому, знайдеться така точка

Теорему доведено.

Теорема 10.5 (Про границю відношення двох функцій в термінах відношення їх похідних). Нехай функці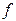ї і 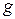означені в деякому околі точки 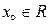, в якій вони дорівнюють нулю та мають скінчені похідні, причому похідна другої функції відмінна від нуля. Тоді існує границя частки першої функції на другу в цій точці, причому ця границя дорівнює відношенню похідних першої функції на другу, обчислених у даній точці. Тобто,

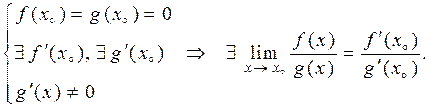
Доведення. За умовою теореми 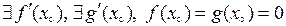, причому . Тому, за означенням похідної функції та за теоремою 5.4 про збереження арифметичних операцій при взятті границі, маємо:

Теорему доведено.

Теорема 10.6 (Лопіталя).

Доведення. Розглянемо тільки випадок скінченої границі . Покладемо: 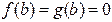. Тоді для довільного 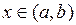функці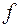ї і 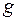задовольняють умові теореми Коші на відрізку 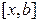. Тому, за умовою існування границі 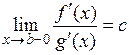випливає, що

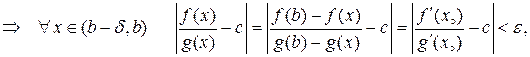
так як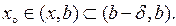

Отже, існує границя 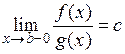, що і потрібно було довести.

Завдання для самостійної роботи10.1: Довести попередню теорему у випадку .

Завдання для самостійної роботи 10.2: Сформулювати теорему 10.6 словесно.

Зауваження10.2. Теорема Лопіталя справджується і якщо:

1) замінити умову існування границі на правому кінці інтервалу на умову її існування в його лівому кінці або у якись внутрішній точці;

2) в теоремі замінити тип невизначеності 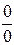на 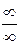, тобто, якщо вимагати існування границі якогось певного знаку чи взагалі. Теж саме стосується лівої точки або внутрішньої точки інтервалу відповідно до першого пункту зауваження.

Приклад 10.3. Обчислимо границю 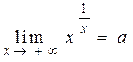. Застосувавши основну логарифмічну тотожність, та за неперервністю експоненти, отримаємо:

.

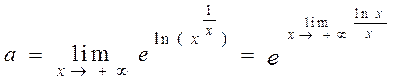Очевидно, що функції 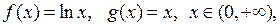задовольняють умовам теореми Лопіталя, тому: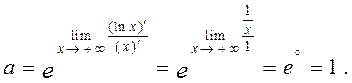

Дата добавления: 2014-01-07