Методы штрафных и барьерных функций

Методы решения задач нелинейного, в частности выпуклого, программирования, при использовании которых данную задачу можно свести к задаче минимизации некоторой специальной функции, представляющей собой сумму данной минимизируемой функции и некоторой другой функции (называемой штрафной), сформированной из ограничительных функций данной задачи, называют методами штрафных функций. Идея этих методов состоит в замене целевой функции данной задачи некоторой обобщенной функцией, значения которой совпадают со значениями исходной функции внутри допустимой области, но при приближении к границе области, а тем более при выходе из нее резко возрастают за счет второго слагаемого обобщенной функции — штрафной функции. Штрафные функции строятся таким образом, что обеспечивают либо быстрое возвращение в допустимую область, либо невозможность выхода из нее. Методы штрафных функций сводят задачу на условный экстремум к решению последовательности задач на безусловный экстремум, что нередко оказывается значительно проще. Эффективность такого подхода становится особенно ощутимой, когда ограничения исходной задачи заданы нелинейными функциями. В зависимости от способа формирования штрафных функций различают метод штрафных и метод барьерных функций.

Рассмотрим метод штрафных функций. Пусть требуется минимизировать функцию

z = f (x) (7.81)

при ограничениях

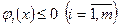(7.82)

Предполагаем, что ограничения х≥0 включены в ограничения (7.82). Функция 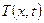, обобщенная для функции (7.81), имеет вид

, (7.83)

где t — некоторое положительное число, называемое коэффициентом штрафа; 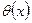— непрерывная функция штрафа, удовлетворяющая условиям: 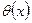=0 для всех точек х допустимой области и 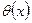>0 для всех остальных точек.

Хорошо изучены штрафные функции видов:

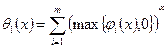
(где α=1; α=2) и

.

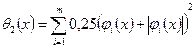Процедура оптимизационного поиска по методу штрафных функций состоит в следующем. Рассматривается некоторая неограниченная, монотонно возрастающая последовательность { t_k } (k =l,2,...) положительных чисел. Для первого числа t ₁ этой последовательности находится точка x ₁^*, доставляющая минимум функции (7.83). Найденная точка x ₁^* используется как начальное приближение для решения задачи поиска минимума функции Т (х, t ₂), где t ₂> t ₁ и т. д. Таким образом решается последовательность задач минимизации функции Т (х, t_k) (k =l, 2,...), причем результат предыдущей оптимизации x_k ^* используется в качестве начального приближения для поиска x_{k+ 1}^*. Поскольку для бесконечно возрастающей последовательности { t_k } локальные минимумы приближаются к допустимой области, то последовательность { x_k ^*} (k =1, 2,...) сходится к локальному оптимуму функции f (x), расположенному внутри или на границе допустимой области. Точки x_k ^* расположены вне допустимой области, поэтому метод штрафных функций называют также методом внешней точки. В этом методе любая точка может быть выбрана в качестве начальной, что значительно упрощает машинное программирование алгоритма решения задачи.

Рассмотрим теперь метод барьерных функций. Если ограничения (7.82) имеют вид строгих неравенств, то для формирования обобщенной функции используются так называемые барьерные функции I (х), значения которых не­ограниченно возрастают при приближении к границе допустимой области. Обобщенная функция U (х, r) имеет вид

U (x, r)= f (x)+ rI(x), (7.84)

где r — некоторое положительное число.

Барьерная функция I (х) должна быть непрерывной во всех точках, лежащих внутри допустимой области, и если { x_k ^*} (k =1, 2,...) — последовательность внутренних точек, сходящихся к граничной точке допустимой области, то последовательность { Ix_k ^*} значений барьерной функции неограниченно возрастает. Поскольку все точки последовательности лежат в допустимой области, метод барьерных функций называют также методом внутренней точки.

В качестве барьерной часто применяется логарифмическая функция вида

,

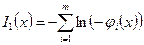определенная только внутри допустимой области. Она неограниченно возрастает при приближении к границе допустимой области.

Используется также более простая функция

,

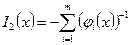называемая обратной и определенная всюду, за исключением границы допустимой области.

Штрафная добавка rI (x) к целевой функции f (x) в равенстве (7.84) образует как бы барьер, препятствующий выходу из допустимой области.

В алгоритме оптимизационного поиска используется последовательность { r_k } положительных чисел r_k (k=1, 2,...), монотонно сходящаяся к нулю. В качестве начальной точки берут произвольную внутреннюю точку хо допустимой области. Она является исходной для поиска точки минимума 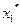обобщенной функции U (x, r ₁). Точка 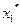используется в качестве начального приближения для поиска точки минимума функции U (x, r ₂) и т. д. Последовательность {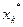} полученных таким образом точек безусловных минимумов функций U (х, r_k) сходится к точке минимума х ^* функции f (x) задачи. Приближение точек 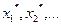к оптимальной точке х ^* осуществляется внутри допустимой области. При уменьшении r убывает влияние штрафной добавки rI (х) в равенстве (7.84) и возрастает влияние целевой функции f (x) задачи. Поэтому последовательность функций U (x, r_k) дает сколь угодно точное (для достаточно большего номера k) приближение к локальному минимуму функции f (x). Если искомый экстремум лежит внутри допустимой области, то решение может быть получено после нескольких первых значений параметра r.

Трудности в расчетах возрастают при определении начальной точки хо внутри допустимой области. Поиск усложняется, если экстремум достигается на границе области. Поскольку значения обобщенной функции при приближении к границе области определяются главным образом величиной барьерной функции, экстремум не всегда может быть вычислен с заданной точностью.

Библиография

1. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б., Математическое программирование, М.: Высшая школа, 1980.

2. Акулич И.Л. Математическое программирование в примерах и задачах, М.: Высшая школа, 1986.

Дата добавления: 2014-01-07