Лекция 10. Множественная нелинейная регрессия

Иногда, при проведении анализа линейной модели, исследователь получает данные о ее неадекватности. В этом случае, его по-прежнему интересует зависимость между предикторными переменными и откликом, но для уточнения модели в ее уравнение добавляются некоторые нелинейные члены. Самым удобным способом оценивания параметров полученной регрессии является нелинейное оценивание. Нелинейное оценивание оставляет выбор характера зависимости за вами. Например, вы можете определить зависимую переменную как логарифмическую функцию от предикторной переменной, как степенную функцию, или как любую другую композицию элементарных функций от предикторов.

Если нет каких-то дополнительных соображений о виде нелинейной зависимости, то математическая модель объекта в многофакторных задачах записывается в виде полинома некоторой степени (в зависимости от требуемой точности):

Выбор степени полиномиального уравнения регрессии зависит также от числа экспериментальных значений, так как количество определяемых коэффициентов уравнения не должно превышать это число.

Чаще всего применяется уравнение второго порядка вида:

.

Для определения коэффициентов такого уравнения применение метода наименьших квадратов приводит к решению достаточно большой системы линейных уравнений, поэтому применяются различные специализированные пакеты обработки информации.

Пример. Имеются данные о деятельности крупнейших компаний США в 1996 г., а именно зависимость чистого дохода (y) от оборота капитала (x ₁), использованного капитала (x ₂) и численности служащих (x ₃, тыс. чел.). Финансовые величины в млрд долларов США.

№	x 1	x 2	x 3	y	yr (лин)	(y – yr)		yr (2-го)	(y – yr)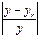
	6,9	83,6			6,252051	-0,25205	0,042009	6,00872	-0,00872	0,001453
		6,5			2,099069	0,900931	0,30031	2,579707	0,420293	0,140098
	107,9	50,4		6,5	5,517332	0,982668	0,15118	6,523279	-0,02328	0,003581
	16,7	15,4	45,2	3,3	2,604077	0,695923	0,210886	2,531778	0,768222	0,232795
	79,6	29,6	299,3	0,1	3,317273	-3,21727	32,17273	1,281566	-1,18157	11,81566
	16,2	13,3	41,6	3,6	2,478957	1,121043	0,311401	2,442586	1,157414	0,321504
	5,9	5,9	17,8	1,5	1,992625	-0,49263	0,328417	1,650353	-0,15035	0,100235
	53,1	27,1		5,5	3,356091	2,143909	0,389802	4,26106	1,23894	0,225262
	18,1	11,2	82,3	2,4	2,245045	0,154955	0,064565	2,095893	0,304107	0,126711
	35,3	16,4			2,666353	0,333647	0,111216	3,019538	-0,01954	0,006513
	71,9	32,5	225,4	4,2	3,646015	0,553985	0,131901	3,666293	0,533707	0,127073
	93,6	25,4		2,7	2,07406	0,62594	0,23183	2,510282	0,189718	0,070266
		6,4	43,8	1,6	1,984669	-0,38467	0,240418	1,816628	-0,21663	0,135392
	31,5	12,5	102,3	2,4	2,390002	0,009998	0,004166	2,62782	-0,22782	0,094925
	36,7	14,3		3,3	2,542114	0,757886	0,229663	2,734789	0,565211	0,171276
	13,8	6,5	49,1	1,8	2,010093	-0,21009	0,116719	2,137662	-0,33766	0,18759
	64,8	22,7	50,4	2,4	3,485497	-1,0855	0,45229	1,954655	0,445345	0,185561
	30,4	15,8		1,6	1,470948	0,129052	0,080658	1,765629	-0,16563	0,103518
	12,1	9,3		1,4	2,104745	-0,70475	0,50339	1,613623	-0,21362	0,152588
	31,3	18,9		0,9	2,962984	-2,06298	2,292204	3,978139	-3,07814	3,420154
S	753,8	423,7	2921,2	57,2	S^2	26,31992	38,36575	S^2	15,75306	17,62216

Сначала определяем параметры множественного линейного уравнения. В результате применения процедуры Регрессия \ Анализ данных получены следующие значения: b ₀ = 1,622593; b ₁ = 0,009165; b ₂ = 0,06246; b ₃ = –0,00295, т.е. уравнение имеет вид: y = 1,622593 + 0,009165 × x ₁ + 0,06246 × x ₂ – 0,00295 × x ₃.

Расчетные значения по этому уравнению приведены в соответствующем столбце таблицы. Статистические характеристики. Общая сумма квадратов:

.

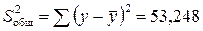Остаточная сумма квадратов:

.

Факторная:

.

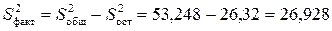Факторная дисперсия на одну степень свободы s ²_факт = 26,928/3 = 8,976. Остаточная дисперсия на одну степень свободы s ²_ост и вытекающая из нее стандартная ошибка s _ост:

.

Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F -отношения, т.е. критерий F:

.

Табличное значение критерия Фишера при уровне значимости 0,05 и числах степеней свободы 3 и 16 равно 3,239, следовательно полученное уравнение адекватно.

Индекс множественной корреляции:

.

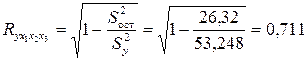Коэффициент детерминации:

.

Критерий Фишера по формуле (3.32):

.

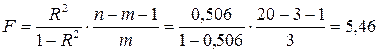Величина скорректированного индекса детерминации

.

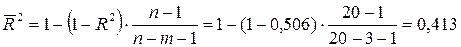Средняя ошибка аппроксимации A = (38,37 / 20) × 100 = 191,8 %. Или:

.

Теперь переходим к нелинейному уравнению множественной регрессии, в качестве которого выбираем полный полином второго порядка:

Для определения коэффициентов такого уравнения средствами Excel необходимо дополнительно сформировать 6 столбцов для расчета коэффициентов от b ₁₁ до b ₂₃. После этого применяем процедуру Регрессия \ Анализ данных. Результаты в следующей таблице:

b0	1,652758
b1	0,136992
b2	–0,13307
b3	–0,01089
b11	–0,00382
b22	0,003756
b33	1,69E-05
b12	0,006021
b13	0,000327
b23	–0,00075

Расчетные значения по этому уравнению приведены в соответствующем столбце таблицы. Статистические характеристики. Общая сумма квадратов:

.

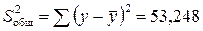Остаточная сумма квадратов:

.

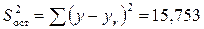Факторная:

.

Факторная дисперсия на одну степень свободы s _факт = 37,495/9 = 4,166. Остаточная дисперсия на одну степень свободы s ²_ост и вытекающая из нее стандартная ошибка s _ост:

.

Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F -отношения, т.е. критерий F:

.

Табличное значение критерия Фишера при уровне значимости 0,05 и числах степеней свободы 9 и 10 равно 3,02, следовательно, полученное уравнение неадекватно.

Индекс множественной корреляции:

.

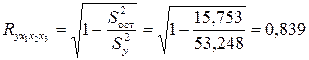Коэффициент детерминации:

.

Критерий Фишера по формуле (3.32):

.

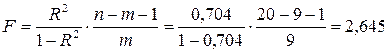Величина скорректированного индекса детерминации

.

Средняя ошибка аппроксимации A = (17,62 / 20) × 100 = 88,11 %. Или:

.

Для полученных уравнений 1-го и 2-го порядков можно подсчитать все статистические характеристики, как в примере для линейной множественной регрессии: частный F -критерий, ошибки в определении коэффициентов и значения критериев Стьюдента для каждого из них, уравнение регрессии в стандартизованном масштабе и его статистические характеристики.

Большинство этих значений получаются в процедуре Регрессия.

Дата добавления: 2014-01-07